Distance euclidienne vs corrélation de Pearson vs similarité de cosinus?
Leurs objectifs sont les mêmes: trouver des vecteurs. Quelle situation utilisez-vous? (aucun des exemples pratiques?)
3 réponses
pearson(X1, X2) == pearson(X1, 2 * X2 + 3). C'est une propriété assez importante parce que souvent vous ne vous souciez pas que deux vecteurs sont similaires en termes absolus, seulement qu'ils varient de la même manière.
la différence entre le Coefficient de corrélation de Pearson et la similarité du cosinus peut être vue à partir de leurs formules:
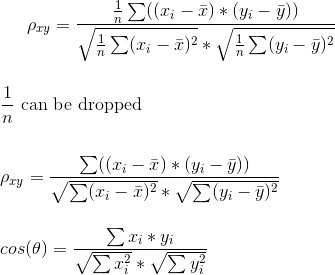
la raison pour laquelle le Coefficient de corrélation de Pearson est invariant à l'addition de n'importe quelle constante est que les moyens sont soustraits par construction. Il est également facile de voir que le Coefficient de corrélation de Pearson et la similarité du cosinus sont équivalents lorsque X et Y signifie 0, donc on peut penser à la corrélation de Pearson Le Coefficient est une version dégradée de la similitude cosinus.
pour une utilisation pratique, considérons les retours des deux actifs x et y:
In [275]: pylab.show()
In [276]: x = np.array([0.1, 0.2, 0.1, -0.1, 0.5])
In [277]: y = x + 0.1
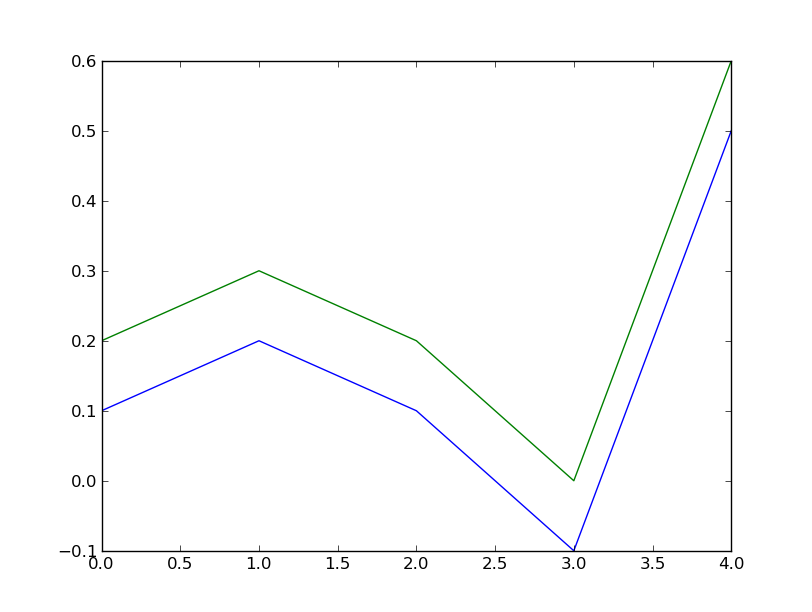
les rendements de ces actifs ont exactement la même variabilité, qui est mesurée par le Coefficient de corrélation de Pearson (1), mais ils ne sont pas exactement semblables, qui est mesurée par la similarité cosinus (0,971).
In [281]: np.corrcoef([x, y])
Out[281]:
array([[ 1., 1.], # The off diagonal are correlations
[ 1., 1.]]) # between x and y
In [282]: from sklearn.metrics.pairwise import cosine_similarity
In [283]: cosine_similarity(x, z)
Out[283]: array([[ 0.97128586]])
en plus de la réponse de @dsimcha, les similitudes cosinus d'un sous-ensemble des données originales sont les mêmes que celles des données originales, ce qui n'est pas vrai pour la corrélation de Pearson. Cela peut être utile lors du regroupement de sous-ensembles de vos données: ils sont (topologiquement) identiques au regroupement original, de sorte qu'ils peuvent être visualisés et interprétés plus facilement