Extraction efficace de tous les sous-polygones générés par des fonctions auto-croisées dans un polygone Multipolytique
à partir d'un shapefile contenant un assez grand nombre (environ 20000) de polygones pouvant se chevaucher partiellement, j'aurais besoin d'extraire tous les sous-polygones provenant de l'intersection de leurs différentes "limites".
Dans la pratique, à partir de quelques maquettes de données:
library(tibble)
library(dplyr)
library(sf)
ncircles <- 9
rmax <- 120
x_limits <- c(-70,70)
y_limits <- c(-30,30)
set.seed(100)
xy <- data.frame(
id = paste0("id_", 1:ncircles),
x = runif(ncircles, min(x_limits), max(x_limits)),
y = runif(ncircles, min(y_limits), max(y_limits))) %>%
as_tibble()
polys <- st_as_sf(xy, coords = c(2,3)) %>%
st_buffer(runif(ncircles, min = 1, max = 20))
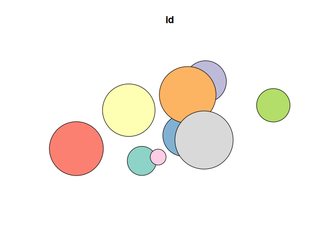
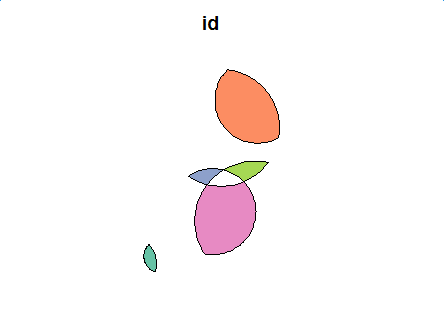
plot(polys[1])
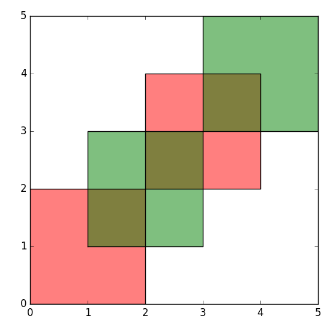
j'aurais besoin de tirer un sf ou sp multipolygon contenant tous et uniquement les polygones générés par les intersections, quelque chose comme:
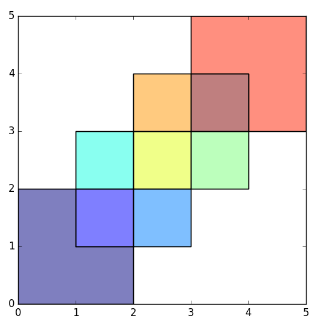
(notez que les couleurs ne sont là que pour illustrer le résultat attendu, dans lequel chaque "couleur différente" de la zone est séparée de polygone qui n'a pas de superposition de tout autre polygone)
je sais que je pourrais m'en sortir en analysant un polygone à la fois, en identifiant et en sauvegardant toutes ses intersections et ensuite "effacer" ces zones qui forment le multipolygon complet et procéder en cycle, mais c'est assez lent.
je pense qu'il devrait y avoir une solution plus efficace pour cela, mais je ne suis pas en mesure de le comprendre, donc toute aide serait appréciée!
(Les deux sf et sp les solutions basées sont les bienvenues)
UPDATE:
a la fin, j'ai découvert que même aller "un polygone à la fois" la tâche est loin d'être simple! J'ai vraiment du mal avec ce problème apparemment "facile"! Tous les conseils? Même une solution lente ou des conseils pour commencer sur un chemin approprié serait apprécié!
UPDATE 2:
peut-être que ceci clarifiera les choses: la fonctionnalité désirée serait similaire à celle décrite ici:
UPDATE 3:
j'ai remis la prime à @shuiping-chen (merci !), dont la réponse correctement résolu le problème sur l'exemple ensemble de données fourni. La" méthode "doit cependant être généralisée aux situations où des intersections" quadruples "ou" n-uple " sont possibles. Je vais essayer de travailler sur cela dans les prochains jours et poster une solution plus générale si je réussis !
3 réponses
ceci a maintenant été implémenté dans le paquet R sf comme résultat par défaut quand st_intersection est appelé avec un seul argument (sf ou sfc), voir https://r-spatial.github.io/sf/reference/geos_binary_ops.html pour les exemples. (Je ne suis pas sûr de la origins le champ contient des index utiles; idéalement, ils devraient pointer vers des index dans x seulement, en ce moment ils se réfèrent en quelque sorte).
Entrée
je modifie un peu les données de la maquette afin d'illustrer la capacité de gérer plusieurs attributs.
library(tibble)
library(dplyr)
library(sf)
ncircles <- 9
rmax <- 120
x_limits <- c(-70,70)
y_limits <- c(-30,30)
set.seed(100)
xy <- data.frame(
id = paste0("id_", 1:ncircles),
val = paste0("val_", 1:ncircles),
x = runif(ncircles, min(x_limits), max(x_limits)),
y = runif(ncircles, min(y_limits), max(y_limits)),
stringsAsFactors = FALSE) %>%
as_tibble()
polys <- st_as_sf(xy, coords = c(3,4)) %>%
st_buffer(runif(ncircles, min = 1, max = 20))
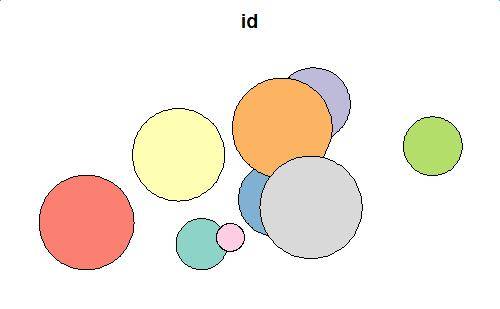
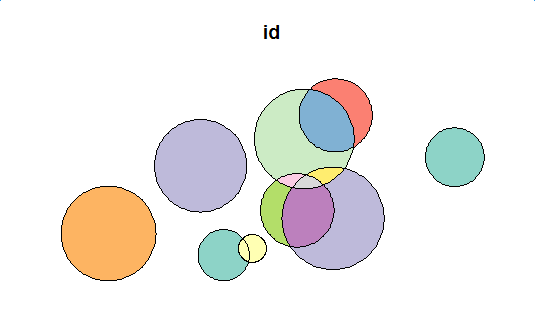
plot(polys[1])
Opération De Base
puis définir les deux fonctions suivantes.
cur: l'index actuel du polygone de basex: l'indice de polygones, qui recoupecurinput_polys: le simple caractéristique des polygoneskeep_columns: le vecteur des noms des attributs nécessaires pour garder après le calcul géométrique
get_difference_region() obtenir la différence entre la base de polygones et d'autres ont recoupé des polygones; get_intersection_region() obtenir les intersections parmi les polygones intersectés.
library(stringr)
get_difference_region <- function(cur, x, input_polys, keep_columns=c("id")){
x <- x[!x==cur] # remove self
len <- length(x)
input_poly_sfc <- st_geometry(input_polys)
input_poly_attr <- as.data.frame(as.data.frame(input_polys)[, keep_columns])
# base poly
res_poly <- input_poly_sfc[[cur]]
res_attr <- input_poly_attr[cur, ]
# substract the intersection parts from base poly
if(len > 0){
for(i in 1:len){
res_poly <- st_difference(res_poly, input_poly_sfc[[x[i]]])
}
}
return(cbind(res_attr, data.frame(geom=st_as_text(res_poly))))
}
get_intersection_region <- function(cur, x, input_polys, keep_columns=c("id"), sep="&"){
x <- x[!x<=cur] # remove self and remove duplicated obj
len <- length(x)
input_poly_sfc <- st_geometry(input_polys)
input_poly_attr <- as.data.frame(as.data.frame(input_polys)[, keep_columns])
res_df <- data.frame()
if(len > 0){
for(i in 1:len){
res_poly <- st_intersection(input_poly_sfc[[cur]], input_poly_sfc[[x[i]]])
res_attr <- list()
for(j in 1:length(keep_columns)){
pred_attr <- str_split(input_poly_attr[cur, j], sep, simplify = TRUE)
next_attr <- str_split(input_poly_attr[x[i], j], sep, simplify = TRUE)
res_attr[[j]] <- paste(sort(unique(c(pred_attr, next_attr))), collapse=sep)
}
res_attr <- as.data.frame(res_attr)
colnames(res_attr) <- keep_columns
res_df <- rbind(res_df, cbind(res_attr, data.frame(geom=st_as_text(res_poly))))
}
}
return(res_df)
}
Premier Niveau
Différence
voyons l'effet de la fonction de différence sur la maquette données.
flag <- st_intersects(polys, polys)
first_diff <- data.frame()
for(i in 1:length(flag)) {
cur_df <- get_difference_region(i, flag[[i]], polys, keep_column = c("id", "val"))
first_diff <- rbind(first_diff, cur_df)
}
first_diff_sf <- st_as_sf(first_diff, wkt="geom")
first_diff_sf
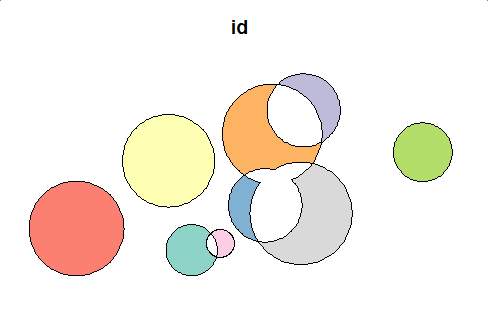
plot(first_diff_sf[1])
Intersection
first_inter <- data.frame()
for(i in 1:length(flag)) {
cur_df <- get_intersection_region(i, flag[[i]], polys, keep_column=c("id", "val"))
first_inter <- rbind(first_inter, cur_df)
}
first_inter <- first_inter[row.names(first_inter %>% select(-geom) %>% distinct()),]
first_inter_sf <- st_as_sf(first_inter, wkt="geom")
first_inter_sf
plot(first_inter_sf[1])
Deuxième Niveau
utiliser l'intersection de premier niveau: entrée, et répétez la même processus.
Différence
flag <- st_intersects(first_inter_sf, first_inter_sf)
# Second level difference region
second_diff <- data.frame()
for(i in 1:length(flag)) {
cur_df <- get_difference_region(i, flag[[i]], first_inter_sf, keep_column = c("id", "val"))
second_diff <- rbind(second_diff, cur_df)
}
second_diff_sf <- st_as_sf(second_diff, wkt="geom")
second_diff_sf
plot(second_diff_sf[1])
Intersection
second_inter <- data.frame()
for(i in 1:length(flag)) {
cur_df <- get_intersection_region(i, flag[[i]], first_inter_sf, keep_column=c("id", "val"))
second_inter <- rbind(second_inter, cur_df)
}
second_inter <- second_inter[row.names(second_inter %>% select(-geom) %>% distinct()),] # remove duplicated shape
second_inter_sf <- st_as_sf(second_inter, wkt="geom")
second_inter_sf
plot(second_inter_sf[1])
récupérez les intersections distinctes du deuxième niveau et utilisez-les comme entrées du troisième niveau. Nous pourrions obtenir que les résultats d'intersection du troisième niveau est NULL, alors le processus devrait prendre fin.
Sommaire
nous mettons toute la différence les résultats dans la liste étroite, et mettre tous les résultats d'intersection dans la liste ouverte. Puis nous avons:
- quand la liste est vide, on arrête le processus
- Le résultat est proche de liste
par conséquent, nous obtenons le code final ici (les deux fonctions de base doivent être déclarées):
# init
close_df <- data.frame()
open_sf <- polys
# main loop
while(!is.null(open_sf)) {
flag <- st_intersects(open_sf, open_sf)
for(i in 1:length(flag)) {
cur_df <- get_difference_region(i, flag[[i]], open_sf, keep_column = c("id", "val"))
close_df <- rbind(close_df, cur_df)
}
cur_open <- data.frame()
for(i in 1:length(flag)) {
cur_df <- get_intersection_region(i, flag[[i]], open_sf, keep_column = c("id", "val"))
cur_open <- rbind(cur_open, cur_df)
}
if(nrow(cur_open) != 0) {
cur_open <- cur_open[row.names(cur_open %>% select(-geom) %>% distinct()),]
open_sf <- st_as_sf(cur_open, wkt="geom")
}
else{
open_sf <- NULL
}
}
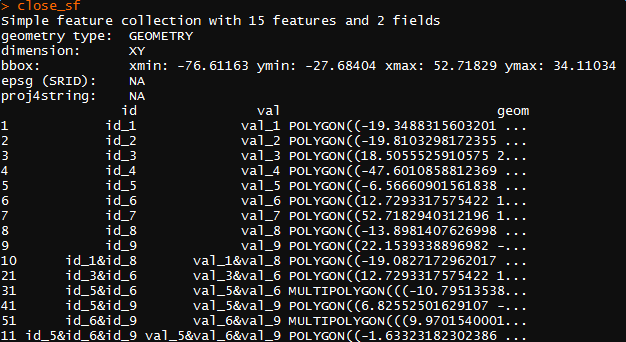
close_sf <- st_as_sf(close_df, wkt="geom")
close_sf
plot(close_sf[1])
Je ne suis pas sûr que cela vous aide car ce n'est pas en R mais je pense qu'il y a un bon moyen de résoudre ce problème en utilisant Python. Il existe une bibliothèque appelée GeoPandas (http://geopandas.org/index.html) qui vous permet de faire facilement des opérations géo. Par étapes, voici ce que vous devez faire:
- Charger tous les Polygones en geopandas GeoDataFrames
- boucle toutes les Géodataframes exécutant une opération de superposition de l'union (http://geopandas.org/set_operations.html)
l'exemple exact est montré dans la documentation.
avant l'opération-2 polygones
après l'opération-9 polygones
s'il y a quelque chose de flou, n'hésitez pas à me le faire savoir! Espérons que cela aide!