Le dessin des mondes de jeu isométrique

mise à Jour: correction de la carte algorithme de rendu, a ajouté plus d'illustrations, changé le formatage.

peut-être l'avantage de la technique "zig-zag" pour la cartographie des tuiles à l'écran peut être dit que les coordonnées x et y de la tuile sont sur les axes verticaux et horizontaux.

"Dessin dans un diamant":

par dessin carte isométrique en utilisant "dessin dans un diamant", qui je crois se réfère à rendre juste la carte en utilisant un emboîté for - boucle sur le tableau bidimensionnel, tel que cet exemple:

tile_map[][] = [[...],...]

for (cellY = 0; cellY < tile_map.size; cellY++):
    for (cellX = 0; cellX < tile_map[cellY].size cellX++):
        draw(
            tile_map[cellX][cellY],
            screenX = (cellX * tile_width  / 2) + (cellY * tile_width  / 2)
            screenY = (cellY * tile_height / 2) - (cellX * tile_height / 2)
        )

avantage:

l'avantage de l'approche est qu'il s'agit d'une simple boucle imbriquée for - avec une logique assez simple en avant qui fonctionne uniformément dans tous les carreaux.

Désavantage:

un inconvénient de cette approche est que les coordonnées x et y des tuiles sur la carte vont augmenter en lignes diagonales, ce qui pourrait rendre plus difficile de cartographier visuellement l'emplacement sur l'écran à la carte représentée comme un tableau:

cependant, il va y avoir un obstacle à la mise en œuvre de ce qui précède exemple de code -- l'ordre de rendu fera que les tuiles qui sont censées être derrière certaines tuiles seront dessinées sur les tuiles devant:

pour corriger ce problème, l'ordre interne de la boucle for doit être inversé -- à partir de la valeur la plus élevée, et le rendu vers la valeur la plus basse:

tile_map[][] = [[...],...]

for (i = 0; i < tile_map.size; i++):
    for (j = tile_map[i].size; j >= 0; j--):  // Changed loop condition here.
        draw(
            tile_map[i][j],
            x = (j * tile_width / 2) + (i * tile_width / 2)
            y = (i * tile_height / 2) - (j * tile_height / 2)
        )

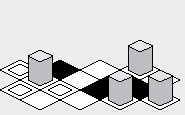
avec la fixation ci-dessus, le rendu de la carte doit être corrigée:

"Zigzag":

avantage:

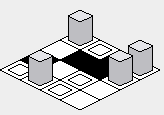
peut-être que l'avantage de l'approche "zig-zag" est que la carte rendue peut sembler un peu plus compacte verticalement que l'approche "diamond":

désavantage:

D'essayer de mettre en œuvre la technique zig-zag, l'inconvénient peut être qu'il est un peu plus difficile d'écrire le code de rendu parce qu'il ne peut pas être écrit aussi simple qu'une boucle for imbriquée sur chaque élément d'un tableau:

tile_map[][] = [[...],...]

for (i = 0; i < tile_map.size; i++):
    if i is odd:
        offset_x = tile_width / 2
    else:
        offset_x = 0

    for (j = 0; j < tile_map[i].size; j++):
        draw(
            tile_map[i][j],
            x = (j * tile_width) + offset_x,
            y = i * tile_height / 2
        )

aussi, il peut être un peu difficile d'essayer de comprendre la coordonnée d'une tuile en raison de le caractère échelonné de l'ordre d'équarrissage:

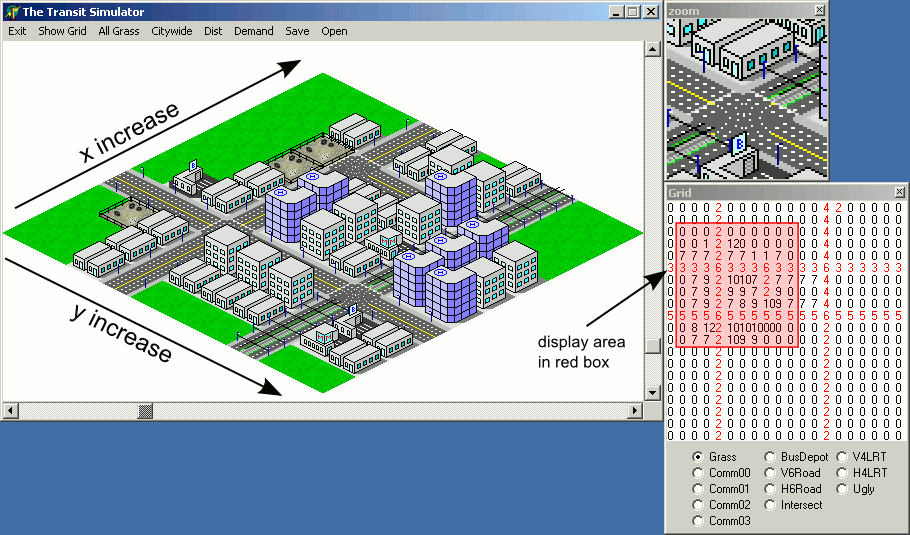
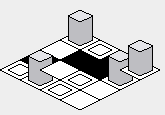
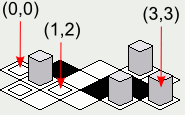
Note: les illustrations incluses dans cette réponse ont été créées avec une implémentation Java du code de rendu des tuiles présenté, avec le tableau suivant int comme la carte:

tileMap = new int[][] {
    {0, 1, 2, 3},
    {3, 2, 1, 0},
    {0, 0, 1, 1},
    {2, 2, 3, 3}
};

les images de la tuile sont:

• tileImage[0] -> Une boîte avec une boîte à l'intérieur.
• tileImage[1] -> une boîte noire.
• tileImage[2] -> une boîte blanche.
• tileImage[3] -> Une boîte avec un grand objet gris.

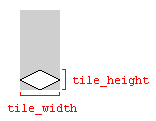
Une Note sur les Carreaux des Largeurs et des Hauteurs

les variables tile_width et tile_height qui sont utilisées dans les exemples de code ci-dessus se rapportent à la largeur et à la hauteur de la tuile de sol dans l'image représentant la tuile:

utilisant les dimensions de l'image fonctionnera, aussi longtemps que les dimensions de l'image et les dimensions de la tuile correspondent. Sinon, la carte des carreaux pourrait être rendue avec des espaces entre les carreaux.