Dessiner des points équidistants sur une spirale
j'ai besoin d'un algorithme pour calculer la distribution des points sur un chemin en spirale.
Les paramètres d'entrée de cet algorithme devrait être:
- largeur de la boucle (distance de la boucle la plus proche)
- distance fixe entre les points
- Le nombre de points à dessiner
la spirale à dessiner est un levier en spirale et les points obtenus doivent être équidistants à partir de chaque autre.
L'algorithme doit imprimer la séquence des coordonnées Cartésiennes des points, par exemple:
Point 1: (0,0) Point 2: (..., ...) ........ Point N (..., ...)
le langage de programmation n'est pas important et toute aide grandement appréciée!
EDIT:
j'ai déjà reçu et modifié cet exemple à partir de ce site:
//
//
// centerX-- X origin of the spiral.
// centerY-- Y origin of the spiral.
// radius--- Distance from origin to outer arm.
// sides---- Number of points or sides along the spiral's arm.
// coils---- Number of coils or full rotations. (Positive numbers spin clockwise, negative numbers spin counter-clockwise)
// rotation- Overall rotation of the spiral. ('0'=no rotation, '1'=360 degrees, '180/360'=180 degrees)
//
void SetBlockDisposition(float centerX, float centerY, float radius, float sides, float coils, float rotation)
{
//
// How far to step away from center for each side.
var awayStep = radius/sides;
//
// How far to rotate around center for each side.
var aroundStep = coils/sides;// 0 to 1 based.
//
// Convert aroundStep to radians.
var aroundRadians = aroundStep * 2 * Mathf.PI;
//
// Convert rotation to radians.
rotation *= 2 * Mathf.PI;
//
// For every side, step around and away from center.
for(var i=1; i<=sides; i++){
//
// How far away from center
var away = i * awayStep;
//
// How far around the center.
var around = i * aroundRadians + rotation;
//
// Convert 'around' and 'away' to X and Y.
var x = centerX + Mathf.Cos(around) * away;
var y = centerY + Mathf.Sin(around) * away;
//
// Now that you know it, do it.
DoSome(x,y);
}
}
mais la disposition du point est fausse, les points ne sont pas équidistants de mutuellement.
l'exemple de distribution correct est l'image à gauche:
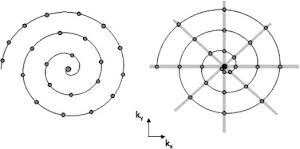
4 réponses
à une première approximation - ce qui est probablement assez bon pour tracer des blocs assez près - la spirale est un cercle et incrémenter l'angle par le rapport chord / radius.
// value of theta corresponding to end of last coil
final double thetaMax = coils * 2 * Math.PI;
// How far to step away from center for each side.
final double awayStep = radius / thetaMax;
// distance between points to plot
final double chord = 10;
DoSome ( centerX, centerY );
// For every side, step around and away from center.
// start at the angle corresponding to a distance of chord
// away from centre.
for ( double theta = chord / awayStep; theta <= thetaMax; ) {
//
// How far away from center
double away = awayStep * theta;
//
// How far around the center.
double around = theta + rotation;
//
// Convert 'around' and 'away' to X and Y.
double x = centerX + Math.cos ( around ) * away;
double y = centerY + Math.sin ( around ) * away;
//
// Now that you know it, do it.
DoSome ( x, y );
// to a first approximation, the points are on a circle
// so the angle between them is chord/radius
theta += chord / away;
}
Cependant, pour une spirale plus lâche, vous aurez à résoudre la distance de chemin plus précisément que les espaces trop large où la différence entre away pour les points successifs est significatif par rapport à chord:
le second la version ci-dessus utilise une étape basée sur la résolution de delta basée sur l'utilisation du rayon moyen pour theta theta+delta:
// take theta2 = theta + delta and use average value of away
// away2 = away + awayStep * delta
// delta = 2 * chord / ( away + away2 )
// delta = 2 * chord / ( 2*away + awayStep * delta )
// ( 2*away + awayStep * delta ) * delta = 2 * chord
// awayStep * delta ** 2 + 2*away * delta - 2 * chord = 0
// plug into quadratic formula
// a= awayStep; b = 2*away; c = -2*chord
double delta = ( -2 * away + Math.sqrt ( 4 * away * away + 8 * awayStep * chord ) ) / ( 2 * awayStep );
theta += delta;
pour des résultats encore meilleurs sur une spirale lâche, utilisez une solution numérique itérative pour trouver la valeur de delta où la distance calculée est à l'intérieur d'une tolérance appropriée.
Contribuer un Python générateur (OP n'a pas de demande spécifique de la langue). Il utilise une approximation similaire à celle de la réponse de Pete Kirkham.
arc est le nombre de points requis distance le long du chemin,