Mise en correspondance bipartite dirigée maximum pondéré permettant le partage des sommets de début et de fin

soit G (U u u V, E) soit un graphe bipartite dirigé pondéré (i.e. U et V sont les deux ensembles de noeuds du graphe bipartite et E contient des arêtes dirigées pondérées de U à V ou de V à U). Voici un exemple:

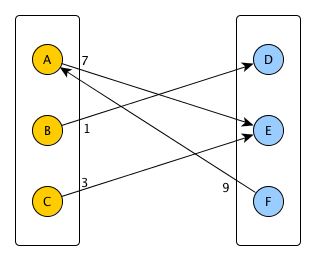
bipartite directed and weighted graph

dans ce cas: 

U = {A,B,C} 
V = {D,E,F} 
E = {(A->E,7), (B->D,1), (C->E,3), (F->A,9)}

définition: correspondance directe (j'ai inventé ce terme juste pour faire des choses adhérent): ensemble d'arêtes orientées peuvent partager le début ou la fin de sommets. C'est-à-dire, si U - >V et U' - >V' appartiennent tous deux à une DirectionalMatching alors V /= U' et V' /= U mais il se peut que U = U' ou V = V'.

Ma question: la Façon la plus efficace de trouver un DirectionalMatching , tel que défini ci-dessus, pour un bipartite directionnelle pondérée graphique qui maximise la somme des poids de ses arêtes?

par efficacement , je veux dire complexité polynomiale ou plus rapide, je sais déjà mettre en œuvre une approche naïve de la force brute.

dans l'exemple au-dessus du maximum pondéré est: {F->A,C->E,B - >D}, avec une valeur de 13.

démontrer formellement l'équivalence de ce problème à tout autre problème bien connu dans la théorie des graphes serait également valable.

Merci!

Note 1: cette question est basée sur correspondance bipartite pondérée avec les bords dirigés mais avec l'assouplissement supplémentaire qu'il est permis pour les bords dans la correspondance pour partager l'origine ou la destination. Puisque cette relaxation fait une grande différence, j'ai créé une question indépendante.

Note 2: il s'agit d'un maximum poids correspondant. La cardinalité (nombre de bords présents) et le nombre de sommets couverts par l'appariement ne sont pas pertinents pour un résultat correct. Seul le poids maximum compte.

Note 2: au cours de mes recherches pour résoudre le problème, j'ai trouvé cet article, je pense qu'il serait utile à d'autres essayant de trouver une solution: alternant des cycles et des chemins dans bord-coloré multigraphes: une enquête

Note 3: La formulation du problème se transformerait alors en: trouver l'ensemble des bords sans couleur-chemins alternatifs ou cycles qui a la somme de poids maximale.

Note 4: je soupçonne que le problème pourrait être NP-dur, mais je ne suis pas que l'expérience avec réductions, donc je n'ai pas réussi à le prouver encore.

encore un autre exemple :

Imaginez que vous aviez

4 sommets: {u1, u2} {v1, v2}

4 arêtes: {u1->v1, u1->v2, u2->v1, v2->u2}

alors, quel que soit leur poids, u1->v2 et v2->u2 ne peuvent pas être dans le même correspondance directe , ne peut pas non plus v2->u2 et u2->v1 . Toutefois u1->v1 et u1->v2 peut, et donc peut u1->v1 et u2->v1 .

21
demandé sur Community 2013-02-12 17:06:23

2 réponses

définit un nouveau graphe non corrigé G' de G comme suit.

  1. G' a un noeud (A, B) avec le poids w pour chaque bord dirigé (A, B) avec le poids w dans G
  2. G' a une arête non dirigée ((A, B),(B, C)) si (A, B) et (B, C) sont deux arêtes dirigées en G

http://en.wikipedia.org/wiki/Line_graph#Line_digraphs

Trouvez maintenant un vertex indépendant maximal (pondéré) défini dans G' .

http://en.wikipedia.org/wiki/Vertex_independent_set

Edit: trucs après ce point ne fonctionne que si l'ensemble de l'arête de poids sont les même lors de l'arête de poids ont des valeurs différentes de ses un problème plus difficile à résoudre (google "poids maximum indépendant vertex set" pour possible algorithmes)

en général, ce serait un problème difficile à résoudre. Cependant, G' est un graphe bipartite -- il ne contient que des cycles égaux. Trouver le vertex indépendant maximal (pondéré) dans un graphe bipartite est et non NP-dur.

l'algorithme que vous exécuterez sur G' est le suivant.

  1. trouver les composants connectés de G' , dire H_1, H_2, ..., H_k
  2. pour chaque H_i faire un 2-coloration (rouge et bleu) des noeuds. L'approche cookbook ici est de faire une recherche en profondeur-première sur H_i couleurs alternées. Une approche simple serait de colorer chaque vertex dans H_i en se basant sur le fait que le bord correspondant dans G va de U à V (rouge) ou de V à U (bleu).
  3. les deux options pour quels noeuds à sélectionnez H_i sont soit de tous les noeuds rouges ou tous les nœuds bleus. Choisissez l'ensemble de noeuds colorés avec un poids plus élevé. Par exemple, l'ensemble de noeuds rouges a un poids égal à H_i.nodes.where(node => node.color == red).sum(node => node.w) . Appeler l'ensemble de noeuds de poids plus élevé N_i .
  4. votre jeu de vertex indépendant pondéré est maintenant union(N_1, N_2, ..., N_k) .

puisque chaque vertex dans G' correspond à un des bords dirigés dans G , vous avez votre maximum DirectionalMatching.

10
répondu Timothy Shields 2013-02-26 03:47:38

ce problème peut être résolu en temps polynomial en utilisant algorithme hongrois . La" preuve " de Vor ci-dessus est fausse.

La méthode de structuration du problème de l'exemple ci-dessus est la suivante: 

   D E F
A  # 7 9  
B  1 # #
C  # 3 #

où "#" signifie l'infini négatif. Vous résolvez ensuite la matrice en utilisant l'algorithme hongrois pour déterminer la correspondance maximale. Vous pouvez multiplier les nombres par -1 si vous voulez trouver un minimum correspondre.

-2
répondu Tyler Durden 2013-02-19 19:16:11