Différence entre la trajectoire hamiltonienne et la trajectoire d'euler
Peut-on me dire la différence entre le chemin hamiltonien et euler chemin. Ils semblent similaires!
8 réponses
Euler chemin est un chemin qui traverse chaque bord exactement une fois sans se répéter, s'il se termine au sommet initial, alors c'est un cycle D'Euler.
chemin Hamiltonien passe à travers chaque sommet (notez pas chaque bord), exactement une fois, si elle se termine au sommet initial alors c'est un cycle Hamiltonien.
dans un chemin D'Euler vous pourriez passer par un sommet plus d'une fois.
dans un chemin Hamiltonien vous ne pouvez pas passer à travers tous bord.
chemin Eulérien doit visiter chaque bord exactement une fois, en chemin Hamiltonien doit visiter chaque sommet exactement une fois.
Théorie Des Graphes Définitions
(par ordre décroissant de généralité)
Marche: une séquence de bords, où la fin d'un bord marque le début de la prochaine arête
Piste: une marche qui ne répète aucun bord. Tous les sentiers de randonnées.
Chemin: une promenade où chaque sommet est traversé exactement une fois. (les chemins utilisés pour se référer à ouvrir promenades, la définition a changé MAINTENANT) la propriété de traverser les sommets une seule fois signifie que les bords sont aussi croisés une seule fois, donc tous les chemins sont des sentiers.
chemins Hamiltoniens et sentiers eulériens
chemin Hamiltonien visites chaque vertex dans le graphique (exactement une fois, parce que c'est un chemin)
sentier eulérien visites chaque arête dans le graphe exactement une fois (parce que c'est un sentier, les sommets peuvent être croisés plus d'une fois.)
un chemin Hamiltonien visite chaque noeud (ou vertex) exactement une fois, et un chemin eulérien traverse chaque bord exactement une fois.
cycles D'Euler visite tous les bord dans le graphique exactement une fois. S'il y a des sommets dans le graphique avec plus de deux arêtes, alors par définition, le cycle passera à travers ces sommets plus d'une fois. En conséquence, les sommets peuvent être répétées mais les bords ne peut pas.
cycles Hamiltoniens visite tous les sommet dans le graphique exactement une fois (semblable au problème du voyageur de commerce). Par conséquent, ni les arêtes ni les sommets ne peuvent être répétés.
je vais utiliser un exemple courant en biologie; reconstruire un génome en faisant des échantillons D'ADN.
assemblée De novo
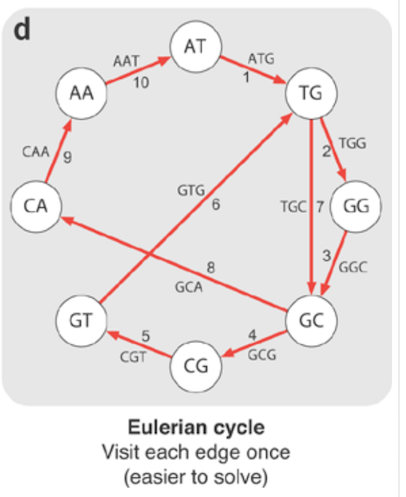
pour construire un génome à partir de courtes lectures, il est nécessaire de construire un graphique de ces lectures. Nous le faisons en fractionnant les lectures en K-mers et en les assemblant en un graphique.
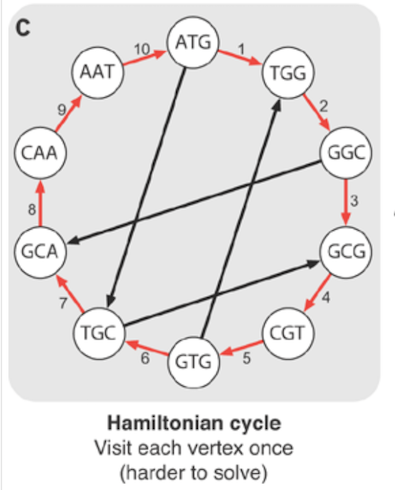
nous pouvons reconstruire le génome en visitant chaque noeud une fois comme dans le diagramme. Ceci est connu comme Voie hamiltonienne.
Une Euler chemin est un chemin qui utilise chaque bord d'une graphique exactement une fois.et il doit avoir exactement deux sommets étranges.le parcours commence et se termine à différents sommet. Un cycle Hamiltonien est un cycle qui contient tous les sommets du graphe par conséquent, vous ne pouvez pas utiliser toutes les arêtes du graphe.
Euler path est un graphe utilisant chaque bord (NOTE) du graphe exactement une fois. Euler circuit est un chemin d'euler qui revient à son point de départ après avoir couvert tous les bords.
alors que hamilton path est un graphe qui couvre tous les sommets(NOTE) exactement une fois. Lorsque ce chemin retourne à son point de départ, il est appelé circuit de hamilton.