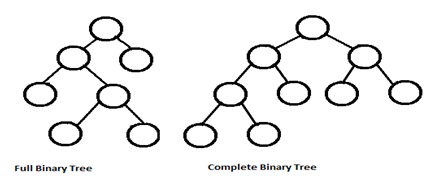
Différence entre "binaire Complet de l'arbre", "strict arbre binaire","plein d'Arbres binaires"?
Je suis confus au sujet de la terminologie des arbres ci-dessous, j'ai étudié l'arbre, et je suis incapable de distinguer entre ces arbres:
A) Arbre Binaire Complet
B) La Stricte Arbre Binaire
C) Arbre Binaire Complet
Aidez-moi à différencier ces arbres. Quand et où ces arbres sont utilisés dans la Structure de données?
10 réponses
Un arbre binaire complet (parfois arbre binaire correct ou arbre à 2 ou arbre strictement binaire) est un arbre dans lequel chaque nœud autre que les feuilles a deux enfants.
Si vous n'avez pas de nœuds avec seulement 1 enfant. Semble être le même que l'arbre binaire strict.
Voici une image d'un arbre binaire complet / strict, de google:
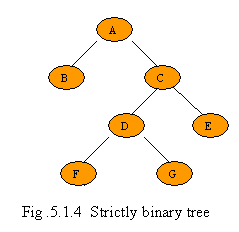
Un arbre binaire complet est un arbre binaire dans lequel chaque niveau, sauf peut-être le dernier, est complètement rempli, et tous les nœuds sont aussi loin à gauche que possible.
Cela semble signifier un arbre équilibré.
Voici une image d'un arbre binaire complet, de google, une partie complète de l'arbre de l'image est bonus.
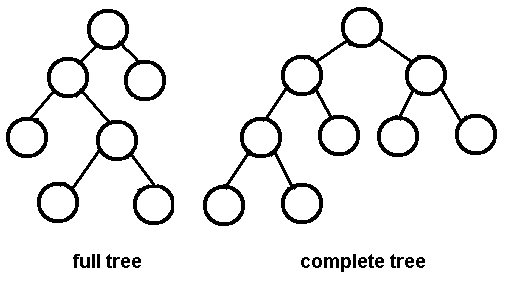
Parfait:
x
/ \
/ \
x x
/ \ / \
x x x x
/ \ / \ / \ / \
x x x x x x x x
Terminé:
x
/ \
/ \
x x
/ \ / \
x x x x
/ \ /
x x x
Stricte:
x
/ \
/ \
x x
/ \
x x
/ \
x x
Il existe une différence entre un arbre binaire STRICT et un arbre binaire complet.
1) PLEIN d'ARBRES BINAIRES: UN arbre binaire de hauteur h qui contient exactement (2^h)-1 éléments est appelé un plein arbre binaire. (Ref: Pg 427, Structures de Données, Algorithmes et Applications en C++ [University Press], Deuxième Édition par Sartaj Sahni).
, Ou en d'autres termes
Dans un arbre binaire complet, chaque nœud a exactement 0 ou 2 enfants et tous les nœuds feuilles sont sur le même niveau.
Par exemple: ce qui suit est un arbre binaire complet:
18
/ \
15 30
/ \ / \
40 50 100 40
2) arbre binaire STRICT: chaque nœud a exactement 0 ou 2 enfants.
Par exemple: ce qui suit est un arbre binaire STRICT:
18
/ \
15 30
/ \
40 50
Je pense qu'il n'y a pas de confusion dans la définition d'un arbre binaire complet, encore pour l'exhaustivité du post, je voudrais dire ce qu'est un arbre binaire complet.
3) arbre binaire complet: un arbre binaire est complet Arbre binaire si tous les niveaux sont complètement remplis sauf peut-être le dernier niveau et le dernier niveau a toutes les clés aussi à gauche que possible.
Par exemple: ce qui suit est un arbre binaire complet:
18
/ \
15 30
/ \ / \
40 50 100 40
/ \ /
8 7 9
Note: ce qui suit est également un arbre binaire complet:
18
/ \
15 30
/ \ / \
40 50 100 40
Avertissement- La principale source de certaines définitions sont wikipedia, toute suggestion pour améliorer ma réponse est la bienvenue.
Bien que ce post ait une réponse acceptée et qu'il soit bon, j'étais toujours dans la confusion et je voudrais ajouter quelques précisions concernant la différence entre ces termes.
(1)arbre binaire complet - un arbre binaire complet est un arbre binaire dans lequel chaque nœud autre que les feuilles a deux enfants.Il est également appelé strictement arbre binaire.
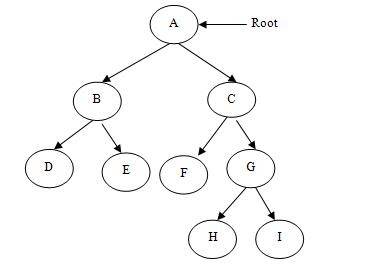
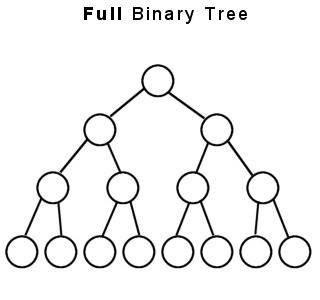
Les deux ci-dessus sont les exemples d'arbre complet ou strictement binaire.
(2)arbre binaire complet - Maintenant, La définition de l'arbre binaire complet est assez ambiguë, elle stipule: - un arbre binaire complet est un arbre binaire dans lequel chaque niveau, sauf peut-être le dernier, est complètement rempli, et tous les nœuds sont aussi à gauche que possible. il peut avoir entre 1 et 2h nœuds, aussi loin que possible à gauche, au dernier niveau h
Notez les lignes en italique.
L'ambiguïté réside dans les lignes en italique, "sauf éventuellement le dernier" ce qui signifie que le dernier niveau peut également être complètement rempli, c'est-à-dire que cette exception n'a pas toujours besoin d'être satisfaite. Si l'exception ne tient pas, c'est exactement comme la deuxième image que j'ai postée, qui peut également être appelée perfect Binary tree. Ainsi, un arbre binaire parfait est également complet et complet mais pas vice-versa, ce qui sera clair par une définition de plus Je dois dire:
Arbre binaire presque complet - Lorsque l'exception dans la définition de l'arbre binaire complet tient alors il est appelé arbre binaire presque complet ou arbre binaire presque complet . C'est juste un type d'arbre binaire complet lui-même , mais une définition distincte est nécessaire pour le rendre plus univoque.
Donc, un arbre binaire presque complet ressemblera à ceci, vous pouvez voir dans l'image que les nœuds sont aussi à gauche que possible, donc c'est plus comme un sous-ensemble de arbre binaire complet, pour dire plus rigoureusement chaque arbre binaire presque complet est un arbre binaire complet mais pas vice versa . :
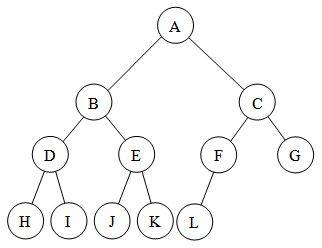
En conclusion des réponses ci-dessus, voici la différence exacte entre les arbres binaires complets/strictement, complets et parfaits
-
Arbre complet / strictement binaire : - chaque nœud sauf les nœuds feuille a deux enfants
Arbre binaire complet : - Tous les niveaux sauf le dernier niveau sont complètement remplis et tous les nœuds sont justifiés à gauche.
Parfait arbre binaire :- Chaque nœud à l'exception des nœuds feuilles ont deux enfants, et à chaque niveau (dernier niveau) est complètement rempli.
Considérons un arbre binaire dont les nœuds sont dessinés de manière arborescente. Commencez maintenant à numéroter les nœuds de haut en bas et de gauche à droite. Un arbre complet a ces propriétés:
Si n a des enfants, tous les nœuds numérotés moins de n ont deux enfants.
Si n a un enfant, il doit être l'enfant gauche et tous les nœuds inférieurs à n ont deux enfants. De plus, aucun nœud numéroté supérieur à n n'a d'enfants.
Si n n'a pas d'Enfants, Aucun nœud numéroté supérieur à n a enfant.
Un arbre binaire complet peut être utilisé pour représenter un tas. Il peut être facilement représenté dans la mémoire contiguë sans lacunes (c'est-à-dire que tous les éléments du tableau sont utilisés sauf pour tout espace qui peut exister à la fin).
Plein d'arbres binaires un arbre binaire mais l'inverse n'est pas possible, et si la profondeur de la binaire est n le pas. de nœuds dans l'arbre binaire complet est ( 2^n-1 ). Il n'est pas nécessaire dans l'arbre binaire qu'ont deux enfants, mais dans le binaire complète à chaque nœud n'ont pas ou deux enfants.
Pour commencer avec les bases, il est très important de comprendre l'arbre binaire lui-même pour comprendre différents types de celui-ci.
Un arbre binaire est un arbre si et seulement si :-
- il a un nœud racine, qui peut ne pas avoir de nœuds enfants (0 childnodes, arbre NULL)
- Le nœud racine peut avoir 1 ou 2 nœuds enfants . Chacun de ces nœuds forme un arbre binaire lui-même
- Le nombre de nœuds enfants peut être 0, 1, 2.......pas plus de 2
- Il y a un chemin unique de la racine à tous les autres noeud
Exemple :
X
/ \
X X
/ \
X X
Venir à vos terminologies demandées:
Un arbre binaire est un arbre binaire ( de hauteur h , nous prenons le nœud racine 0 ) si et seulement si :-
Niveau 0-h-1 représentent un arbre binaire complet de hauteur h-1
- un ou plusieurs nœuds de niveau h-1 peuvent avoir 0 ou 1 nœuds enfants
Si j, k sont des nœuds au niveau h-1, alors j a plus de nœuds enfants que k SI et seulement si j est à gauche de k, c'est-à-dire que le dernier niveau (h) peut être une feuille manquante nœuds, cependant ceux présents doivent être décalés vers la gauche
Exemple :
X
/ \
/ \
/ \
X X
/ \ / \
X X X X
/ \ / \ / \ / \
X X X X X X X X
Un arbre binaire est strictement binaire un arbre si et seulement si :-
Chaque nœud a exactement deux nœuds enfants ou aucun nœud
Exemple :
X
/ \
X X
/ \
X X
/ \ / \
X X X X
Un arbre binaire est un arbre binaire complet si et seulement si :-
Chaque nœud feuille a exactement deux nœuds enfants
Tous les nœuds foliaires sont au même niveau
Exemple :
X
/ \
/ \
/ \
X X
/ \ / \
X X X X
/ \ / \ / \ / \
X X X X X X X X
/ \ / \ / \ / \ / \ / \ / \ / \
X X X X X X X X X X X X X X X X
Vous devriez également savoir ce qu'est un binaire parfait l'arbre est?
Un arbre binaire est un arbre binaire parfait si et seulement si :-
Est un arbre binaire complet
- tous les nœuds foliaires sont au même niveau
Exemple :
X
/ \
/ \
/ \
X X
/ \ / \
X X X X
/ \ / \ / \ / \
X X X X X X X X
/ \ / \ / \ / \ / \ / \ / \ / \
X X X X X X X X X X X X X X X X
Eh bien, je suis désolé de ne pas pouvoir poster des images car je n'ai pas 10 de réputation. J'espère que cela vous aide et d'autres!
Dans mon expérience limitée avec l'arbre binaire, je pense:
- Arbre strictement binaire : tous les nœuds sauf les nœuds feuilles ont deux enfants ou n'ont qu'un nœud racine.
- Complète Arbre Binaire: Un arbre binaire de H strictement(ou exactement) contenant 2^H -1 nœuds , il est clair que chaque niveau a le plus de nœuds.
- arbre binaire complet : c'est un arbre binaire dans lequel tous les niveaux, sauf peut-être le dernier, sont complètement remplis, et tous les nœuds sont aussi à gauche que possible.
Plein d'Arbres Binaires est un arbre binaire dans lequel chaque nœud a 0 ou deux enfants. En d'autres termes, chaque nœud de l'arbre sauf les feuilles a exactement deux enfants.
Un Complète arbre binaire est un arbre binaire dans lequel chaque niveau de l'arbre est complètement rempli, à l'exception du dernier niveau. En outre, dans le dernier niveau, les nœuds doivent être attachés à partir de la position la plus à gauche. un arbre binaire complet doit satisfaire aux exigences suivantes conditions:
- Si a, b sont deux nœuds au-dessus du niveau dernier niveau, puis un a plus d'enfants que b si et seulement si a est situé à gauche de b.
- à Partir du nœud racine, le niveau au-dessus du dernier niveau représente un arbre binaire complet de hauteur h-1.
- un ou plusieurs nœuds du dernier niveau peuvent avoir 0 ou 1 enfant.