Déterminer si deux rectangles se chevauchent?

struct rect
{
    int x;
    int y;
    int width;
    int height;
};

bool valueInRange(int value, int min, int max)
{ return (value >= min) && (value <= max); }

bool rectOverlap(rect A, rect B)
{
    bool xOverlap = valueInRange(A.x, B.x, B.x + B.width) ||
                    valueInRange(B.x, A.x, A.x + A.width);

    bool yOverlap = valueInRange(A.y, B.y, B.y + B.height) ||
                    valueInRange(B.y, A.y, A.y + A.height);

    return xOverlap && yOverlap;
}

struct Rect
{
    Rect(int x1, int x2, int y1, int y2)
    : x1(x1), x2(x2), y1(y1), y2(y2)
    {
        assert(x1 < x2);
        assert(y1 < y2);
    }

    int x1, x2, y1, y2;
};

bool
overlap(const Rect &r1, const Rect &r2)
{
    // The rectangles don't overlap if
    // one rectangle's minimum in some dimension 
    // is greater than the other's maximum in
    // that dimension.

    bool noOverlap = r1.x1 > r2.x2 ||
                     r2.x1 > r1.x2 ||
                     r1.y1 > r2.y2 ||
                     r2.y1 > r1.y2;

    return !noOverlap;
}

il est plus facile de vérifier si un rectangle est complètement en dehors de l'autre, donc s'il est soit

à gauche...

(r1.x + r1.width < r2.x)

ou à droite...

(r1.x > r2.x + r2.width)

ou sur le dessus...

(r1.y + r1.height < r2.y)

ou sur le fond...

(r1.y > r2.y + r2.height)

du second rectangle, il ne peut pas entrer en collision avec lui. Donc pour avoir une fonction qui renvoie un booléen dire le temps le rectangles entrent en collision, nous combinons simplement les conditions par ors logique et nier le résultat:

function checkOverlap(r1, r2) : Boolean
{ 
    return !(r1.x + r1.width < r2.x || r1.y + r1.height < r2.y || r1.x > r2.x + r2.width || r1.y > r2.y + r2.height);
}

déjà recevoir un résultat positif lors de la toucher seulement, nous pouvons changer le "<" et ">" par "<=" et ">=".

posez-vous la question opposée: Comment puis-je déterminer si deux rectangles ne se croisent pas du tout? Évidemment, un rectangle a complètement à gauche du rectangle B ne se croise pas. Aussi, si Un est complètement à droite. De même, si A est complètement au-dessus de B ou complètement au-dessous de B. Dans tout autre cas, A et B se croisent.

ce qui suit peut avoir des bugs, mais je suis assez confiant sur l'algorithme:

struct Rectangle { int x; int y; int width; int height; };

bool is_left_of(Rectangle const & a, Rectangle const & b) {
   if (a.x + a.width <= b.x) return true;
   return false;
}
bool is_right_of(Rectangle const & a, Rectangle const & b) {
   return is_left_of(b, a);
}

bool not_intersect( Rectangle const & a, Rectangle const & b) {
   if (is_left_of(a, b)) return true;
   if (is_right_of(a, b)) return true;
   // Do the same for top/bottom...
 }

bool intersect(Rectangle const & a, Rectangle const & b) {
  return !not_intersect(a, b);
}

supposons que vous ayez défini les positions et les tailles des rectangles comme ceci:

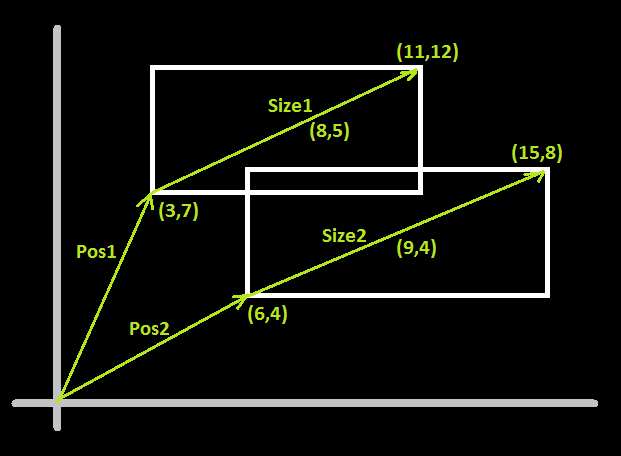
mon implémentation C++ est comme ceci:

class Vector2D
{
    public:
        Vector2D(int x, int y) : x(x), y(y) {}
        ~Vector2D(){}
        int x, y;
};

bool DoRectanglesOverlap(   const Vector2D & Pos1,
                            const Vector2D & Size1,
                            const Vector2D & Pos2,
                            const Vector2D & Size2)
{
    if ((Pos1.x < Pos2.x + Size2.x) &&
        (Pos1.y < Pos2.y + Size2.y) &&
        (Pos2.x < Pos1.x + Size1.x) &&
        (Pos2.y < Pos1.y + Size1.y))
    {
        return true;
    }
    return false;
}

exemple d'appel de fonction selon la figure ci-dessus:

DoRectanglesOverlap(Vector2D(3, 7),
                    Vector2D(8, 5),
                    Vector2D(6, 4),
                    Vector2D(9, 4));

les comparaisons à l'intérieur du bloc if ressembleront à ce qui suit:

if ((Pos1.x < Pos2.x + Size2.x) &&
    (Pos1.y < Pos2.y + Size2.y) &&
    (Pos2.x < Pos1.x + Size1.x) &&
    (Pos2.y < Pos1.y + Size1.y))
                 ↓  
if ((   3   <    6   +   9    ) &&
    (   7   <    4   +   4    ) &&
    (   6   <    3   +   8    ) &&
    (   4   <    7   +   5    ))

Voici comment c'est fait dans L'API Java:

public boolean intersects(Rectangle r) {
    int tw = this.width;
    int th = this.height;
    int rw = r.width;
    int rh = r.height;
    if (rw <= 0 || rh <= 0 || tw <= 0 || th <= 0) {
        return false;
    }
    int tx = this.x;
    int ty = this.y;
    int rx = r.x;
    int ry = r.y;
    rw += rx;
    rh += ry;
    tw += tx;
    th += ty;
    //      overflow || intersect
    return ((rw < rx || rw > tx) &&
            (rh < ry || rh > ty) &&
            (tw < tx || tw > rx) &&
            (th < ty || th > ry));
}

struct Rect
{
   Rect(int x1, int x2, int y1, int y2)
   : x1(x1), x2(x2), y1(y1), y2(y2)
   {
       assert(x1 < x2);
       assert(y1 < y2);
   }

   int x1, x2, y1, y2;
};

//some area of the r1 overlaps r2
bool overlap(const Rect &r1, const Rect &r2)
{
    return r1.x1 < r2.x2 && r2.x1 < r1.x2 &&
           r1.y1 < r2.y2 && r2.x1 < r1.y2;
}

//either the rectangles overlap or the edges touch
bool touch(const Rect &r1, const Rect &r2)
{
    return r1.x1 <= r2.x2 && r2.x1 <= r1.x2 &&
           r1.y1 <= r2.y2 && r2.x1 <= r1.y2;
}

dans la question, vous liez aux maths pour quand les rectangles sont à des angles de rotation arbitraires. Si je comprends le peu sur les angles dans la question cependant, j'interprète que tous les rectangles sont perpendiculaires les uns aux autres.

une connaissance générale de la formule de chevauchement est:

par l'exemple:

   1   2   3   4   5   6

1  +---+---+
   |       |   
2  +   A   +---+---+
   |       | B     |
3  +       +   +---+---+
   |       |   |   |   |
4  +---+---+---+---+   +
               |       |
5              +   C   +
               |       |
6              +---+---+

1) recueillir toutes les coordonnées x (à gauche et à droite) dans une liste, puis la trier et supprimer duplicata

1 3 4 5 6

2) recueillir toutes les coordonnées y (en haut et en bas) dans une liste, puis la trier et supprimer les doublons

1 2 3 4 6

3) Créer un tableau 2D par le nombre de discontinuités entre les coordonnées x uniques * le nombre de discontinuités entre les coordonnées y uniques.

4 * 4

4) peindre tous les rectangles dans cette grille, en augmentant le nombre de chaque cellule, il se produit sur:

   1   3   4   5   6

1  +---+
   | 1 | 0   0   0
2  +---+---+---+
   | 1 | 1 | 1 | 0
3  +---+---+---+---+
   | 1 | 1 | 2 | 1 |
4  +---+---+---+---+
     0   0 | 1 | 1 |
6          +---+---+

5) comme vous peignez les rectangles, il est facile d'intercepter les chevauchements.

disons que les deux rectangles sont rectangle A et rectangle B. Qu'il y ait des centres A1 et B1 (Les coordonnées de A1 et B1 peuvent être facilement trouvées), que les hauteurs soient Ha et Hb, la largeur soit Wa et Wb, que dx soit la largeur(x) la distance entre A1 et B1 et dy soit la hauteur(y) la distance entre A1 et B1.

Maintenant nous pouvons dire que nous pouvons dire que A et B se chevauchent: quand



si(!(dx > Wa+Wb)//!(dy > Ha+Hb)) retourne true

la voie la plus facile est

/**
 * Check if two rectangles collide
 * x_1, y_1, width_1, and height_1 define the boundaries of the first rectangle
 * x_2, y_2, width_2, and height_2 define the boundaries of the second rectangle
 */
boolean rectangle_collision(float x_1, float y_1, float width_1, float height_1, float x_2, float y_2, float width_2, float height_2)
{
  return !(x_1 > x_2+width_2 || x_1+width_1 < x_2 || y_1 > y_2+height_2 || y_1+height_1 < y_2);
}

tout d'abord, placez dans votre esprit que dans les ordinateurs, le système de coordonnées est à l'envers. l'axe des abscisses est le même que celui des mathématiques, mais l'axe des ordonnées augmente vers le bas et diminue vers le haut.. si le rectangle est tiré du centre. si les coordonnées x1 sont supérieures à x2 plus sa moitié de widht. ça veut dire qu'ils se toucheront l'un l'autre. et de la même manière en descendant + la moitié de sa hauteur. il va entrer en collision..

j'ai implémenté une version C#, elle est facilement convertie en C++.

public bool Intersects ( Rectangle rect )
{
  float ulx = Math.Max ( x, rect.x );
  float uly = Math.Max ( y, rect.y );
  float lrx = Math.Min ( x + width, rect.x + rect.width );
  float lry = Math.Min ( y + height, rect.y + rect.height );

  return ulx <= lrx && uly <= lry;
}

ne pensez pas que les coordonnées indiquent où sont les pixels. Pensez à eux comme étant entre les pixels. De cette façon, la surface d'un rectangle 2x2 devrait être 4, Pas 9.

bool bOverlap = !((A.Left >= B.Right || B.Left >= A.Right)
               && (A.Bottom >= B.Top || B.Bottom >= A.Top));

j'ai une solution très facile

soit x1, y1 x2, y2, l1, b1,l2, être des cordinates et leurs longueurs et largeurs respectivement

considérer la condition ((x2

maintenant,la seule façon dont ces rectangles se chevaucheront est si le point diagonal à x1,y1 sera situé à l'intérieur de l'autre rectangle ou de la même façon le point diagonal à x2, y2 sera situé à l'intérieur de l'autre rectangle. ce qui est exactement la condition ci-dessus implique.

A et B être deux rectangle. C être leur rectangle de couverture.

four points of A be (xAleft,yAtop),(xAleft,yAbottom),(xAright,yAtop),(xAright,yAbottom)
four points of A be (xBleft,yBtop),(xBleft,yBbottom),(xBright,yBtop),(xBright,yBbottom)

A.width = abs(xAleft-xAright);
A.height = abs(yAleft-yAright);
B.width = abs(xBleft-xBright);
B.height = abs(yBleft-yBright);

C.width = max(xAleft,xAright,xBleft,xBright)-min(xAleft,xAright,xBleft,xBright);
C.height = max(yAtop,yAbottom,yBtop,yBbottom)-min(yAtop,yAbottom,yBtop,yBbottom);

A and B does not overlap if
(C.width >= A.width + B.width )
OR
(C.height >= A.height + B.height) 

Il prend soin de tous les cas possibles.

extrait de l'exercice 3.28 du livre Introduction to Java Programming - Comprehensive Edition. Le code vérifie si les deux rectangles sont des indenticles, si l'un est à l'intérieur de l'autre et si l'un est à l'extérieur de l'autre. Si aucune de ces conditions sont réunies, les deux se superposent.

* * 3.28 (géométrie: deux rectangles) Écrire un programme qui invite l'utilisateur à entrer dans le centre x -, y-coordonnées, largeur et hauteur de deux rectangles et détermine si le second rectangle est à l'intérieur du Premier ou se chevauche avec le premier, comme indiqué dans la Figure 3.9. Testez votre programme pour couvrir tous les cas. Voici les exemples:

entrez les coordonnées x, y, la largeur et la hauteur du centre de r1: 2,5 4 2,5 43 Entrer le centre de r2 X -, Y-coordonnées, largeur et hauteur: 1.5 5 0.5 3 r2 est à l'intérieur de r1

inscrire le centre x de r1, les coordonnées y, la largeur et la hauteur: 1 2 3 5.5 Entrez les coordonnées X-, y-du centre de r2, la largeur et la hauteur: 3 4 4.5 Cinq R2 chevauche r1

inscrire le centre x de r1, les coordonnées y, la largeur et la hauteur: 1 2 3 3 Entrez les coordonnées X-, y-du centre de r2, la largeur et la hauteur: 40 45 3 2 r2 ne se chevauche pas R1

import java.util.Scanner;

public class ProgrammingEx3_28 {
public static void main(String[] args) {
    Scanner input = new Scanner(System.in);

    System.out
            .print("Enter r1's center x-, y-coordinates, width, and height:");
    double x1 = input.nextDouble();
    double y1 = input.nextDouble();
    double w1 = input.nextDouble();
    double h1 = input.nextDouble();
    w1 = w1 / 2;
    h1 = h1 / 2;
    System.out
            .print("Enter r2's center x-, y-coordinates, width, and height:");
    double x2 = input.nextDouble();
    double y2 = input.nextDouble();
    double w2 = input.nextDouble();
    double h2 = input.nextDouble();
    w2 = w2 / 2;
    h2 = h2 / 2;

    // Calculating range of r1 and r2
    double x1max = x1 + w1;
    double y1max = y1 + h1;
    double x1min = x1 - w1;
    double y1min = y1 - h1;
    double x2max = x2 + w2;
    double y2max = y2 + h2;
    double x2min = x2 - w2;
    double y2min = y2 - h2;

    if (x1max == x2max && x1min == x2min && y1max == y2max
            && y1min == y2min) {
        // Check if the two are identicle
        System.out.print("r1 and r2 are indentical");

    } else if (x1max <= x2max && x1min >= x2min && y1max <= y2max
            && y1min >= y2min) {
        // Check if r1 is in r2
        System.out.print("r1 is inside r2");
    } else if (x2max <= x1max && x2min >= x1min && y2max <= y1max
            && y2min >= y1min) {
        // Check if r2 is in r1
        System.out.print("r2 is inside r1");
    } else if (x1max < x2min || x1min > x2max || y1max < y2min
            || y2min > y1max) {
        // Check if the two overlap
        System.out.print("r2 does not overlaps r1");
    } else {
        System.out.print("r2 overlaps r1");
    }

}
}

bool Square::IsOverlappig(Square &other)
{
    bool result1 = other.x >= x && other.y >= y && other.x <= (x + width) && other.y <= (y + height); // other's top left falls within this area
    bool result2 = other.x >= x && other.y <= y && other.x <= (x + width) && (other.y + other.height) <= (y + height); // other's bottom left falls within this area
    bool result3 = other.x <= x && other.y >= y && (other.x + other.width) <= (x + width) && other.y <= (y + height); // other's top right falls within this area
    bool result4 = other.x <= x && other.y <= y && (other.x + other.width) >= x && (other.y + other.height) >= y; // other's bottom right falls within this area
    return result1 | result2 | result3 | result4;
}

pour ceux d'entre vous qui utilisent des points centraux et des demi-tailles pour leurs données rectangulaires, au lieu des X,y,w,h, ou x0,y0,x1,x1 typiques, voici comment vous pouvez le faire:

#include <cmath> // for fabsf(float)

struct Rectangle
{
    float centerX, centerY, halfWidth, halfHeight;
};

bool isRectangleOverlapping(const Rectangle &a, const Rectangle &b)
{
    return (fabsf(a.centerX - b.centerX) <= (a.halfWidth + b.halfWidth)) &&
           (fabsf(a.centerY - b.centerY) <= (a.halfHeight + b.halfHeight)); 
}

"si vous effectuez la soustraction X ou y coordonnées correspondant aux sommets des deux faisant face à chaque rectangle, si les résultats sont le même signe, les deux rectangles ne se chevauchent pas axes que" (je suis désolé, Je ne suis pas sûr que ma traduction est correcte)

Source: http://www.ieev.org/2009/05/kiem-tra-hai-hinh-chu-nhat-chong-nhau.html

code Java pour déterminer si des Rectangles entrent en contact ou se chevauchent

...

        for (int i = 0;i < n;i++) {
          for (int j = 0;j < n; j++) {
            if (i != j) {
                Rectangle rectangle1 = rectangles.get(i);
                Rectangle rectangle2 = rectangles.get(j);

                int l1 = rectangle1.l; //left
                int r1 = rectangle1.r; //right
                int b1 = rectangle1.b; //bottom
                int t1 = rectangle1.t; //top

                int l2 = rectangle2.l;
                int r2 = rectangle2.r;
                int b2 = rectangle2.b;
                int t2 = rectangle2.t;

                boolean topOnBottom = t2 == b1;
                boolean bottomOnTop = b2 == t1;
                boolean topOrBottomContact = topOnBottom || bottomOnTop;

                boolean rightOnLeft = r2 == l1;
                boolean leftOnRight = l2 == r1;
                boolean rightOrLeftContact = leftOnRight || rightOnLeft;

                boolean leftPoll = l2 <= l1 && r2 >= l1;
                boolean rightPoll = l2 <= r1 && r2 >= r1;
                boolean leftRightInside = l2 >= l1 && r2 <= r1;
                boolean leftRightPossiblePlaces = leftPoll || rightPoll || leftRightInside;

                boolean bottomPoll = t2 >= b1 && b2 <= b1;
                boolean topPoll = b2 <= b1 && t2 >= b1;
                boolean topBottomInside = b2 >= b1 && t2 <= t1;
                boolean topBottomPossiblePlaces = bottomPoll || topPoll || topBottomInside;


                boolean topInBetween = t2 > b1 && t2 < t1;
                boolean bottomInBetween = b2 > b1 && b2 < t1;
                boolean topBottomInBetween = topInBetween || bottomInBetween;

                boolean leftInBetween = l2 > l1 && l2 < r1;
                boolean rightInBetween = r2 > l1 && r2 < r1;
                boolean leftRightInBetween = leftInBetween || rightInBetween;

                if ( (topOrBottomContact && leftRightPossiblePlaces) || (rightOrLeftContact && topBottomPossiblePlaces) ) {
                    path[i][j] = true;
                }
            }
        }
    }

...

Cette réponse doit être la première réponse:

si les rectangles se chevauchent, la zone de chevauchement sera supérieure à zéro. Maintenant, trouvons la zone de chevauchement:

s'ils se chevauchent, alors le bord gauche du chevauchement-rect sera le max(r1.x1, r2.x1)et le bord droit sera min (R1.x2, r2.x2). ainsi la longueur du chevauchement sera min (r1.x2, r2.x2) - max (r1.x1, r2.x1)

ainsi la zone sera: zone = (max (R1.x1, r2.x1) - min(r1.x2, r2.x2)) * (max(R1.y1, r2.Y1) - min (R1.y2, r2.y2))

si = 0 alors ils ne se chevauchent. Simple n'est-ce pas?