Concevoir Dfa acceptant des chaînes binaires divisibles par un nombre 'n'

ci-dessous, j'ai écrit une réponse pour n égale à 5, mais vous pouvez appliquer la même approche pour tirer des ADF pour n'importe quelle valeur de n et "n'importe quel système de nombre de position" E. g binaire, ternaire...

premier Adi le terme "Adi complet", un ADI défini sur le domaine complet Dans δ:Q × Σ→Q est appelé "Adi complet". En d'autres termes nous pouvons dire; dans le diagramme de transition de DFA complète il n'y a pas de bord manquant (par exemple de chaque État dans Q il y a un bord sortant présent pour chaque symbole de langue dans Σ). Note: parfois, nous définissons partiel DFA comme étant comment "δ:Q × Σ→Q" lire dans la définition d'un DFA .

Conception DFA accepter des nombres Binaires divisible par le nombre "n":

Step-1 : quand vous divisez un nombre ω par n alors rappel peut être soit 0, 1, ..., (n - 2) ou (n - 1). Si le reste est 0 cela signifie que ω est divisible par n autrement pas. Ainsi, dans mon DFA il y aura un État q _r qui correspondrait à un reste de valeur r , où 0 <= r <= (n - 1) , et le nombre total d'États dans le DFA est n .

Après traitement d'une chaîne de nombres ω Sur Σ, l'état final est q _r implique que ω % n => r (% opérateur de rappel).

In n'importe quel automate, le but d'un État est comme un élément de mémoire. Un État dans une atomata stocke quelques informations comme l'interrupteur du ventilateur qui peut dire si le ventilateur est en " off "ou en" on " état. Pour n = 5, cinq états dans le DFA correspondant à cinq informations de rappel comme suit:

1. État q ₀ atteint si le rappel est de 0. L'état q ₀ est l'état final(état d'acceptation). C'est aussi un état initial.
2. État q ₁ atteint si le rappel est 1, un non-état final.
3. État q ₂ si le rappel est de 2, un non-état final.
4. État q ₃ si le rappel est de 3, un non-état final.
5. État q ₄ si le rappel est de 4, un non-état final.

en utilisant les informations ci-dessus, nous pouvons commencer le diagramme de transition de dessin TD de cinq états comme suit:

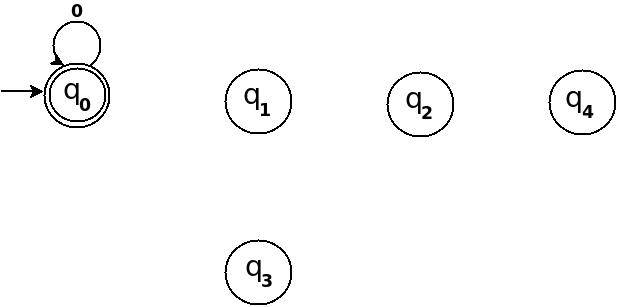
Figure 1

donc, 5 états pour 5 valeurs résiduelles. Après avoir traité une chaîne ω si l'état final devient q ₀ cela signifie que l'équivalent décimal de la chaîne d'entrée est divisible par 5. Dans la figure ci-dessus q ₀ est marqué état final comme deux cercles concentriques.

De plus, j'ai défini une règle de transition δ: (q ₀ , 0)→q ₀ comme une boucle pour le symbole '0' à l'état q ₀ , c'est parce que l'équivalent décimal de toute chaîne se composent de seulement '0' est 0 et 0 est un divisible par n .

Étape 2 : TD ci-dessus est incomplete; and can only process strings of '0' S. Maintenant, ajoutez quelques bords supplémentaires pour qu'il puisse traiter les chaînes de nombres suivantes. Consultez le tableau ci-dessous, montre de nouvelles règles de transition sont ceux qui peut être ajouté à l'étape suivante:

┌──────┬──────┬─────────────┬─────────┐
│Number│Binary│Remainder(%5)│End-state│
├──────┼──────┼─────────────┼─────────┤
│One   │1     │1            │q1       │
├──────┼──────┼─────────────┼─────────┤
│Two   │10    │2            │q2       │
├──────┼──────┼─────────────┼─────────┤
│Three │11    │3            │q3       │
├──────┼──────┼─────────────┼─────────┤
│Four  │100   │4            │q4       │
└──────┴──────┴─────────────┴─────────┘

1. pour traiter la chaîne binaire '1' il devrait y avoir une règle de transition δ: (q ₀ , 1)→q ₁
2. deux: - la représentation binaire est '10' , état final devrait être q ₂ , et '10' , nous avons juste besoin d'ajouter une autre règle de transition δ:(q ₁ , 0)→q ₂
   
   Chemin : →(q ₀ )─1→(q ₁ )─0→(q ₂ )
3. trois: - en binaire il est '11' , état final est q ₃ , et nous devons ajouter une transition la règle δ:(q ₁ , 1)→q ₃
   
   Chemin : →(q ₀ )─1→(q ₁ )─1→(q ₃ )
4. Four: - en binaire '100' , l'état final est q ₄ . TD traite déjà la chaîne de préfixe '10' et nous avons juste besoin d'ajouter une nouvelle règle de transition δ: (q ₂ , 0)→q ₄
   
   Chemin : →(q ₀ )─1→(q ₁ )─0→(q ₂ )─0→(q ₄ )

Figure 2

Étape 3 : Cinq = 101

Le diagramme de transition de la figure 2 ci-dessus est encore incomplet et il y a beaucoup de bords manquants, pour un exemple aucune transition n'est définie pour δ: (q ₂ , 1)- ? . Et la règle doit être présente pour traiter des chaînes comme '101' .

Parce que '101' = 5 est divisible par 5, et pour accepter '101' j'ajouterai δ: (q ₂ , 1)→q ₀ dans la figure ci-dessus-2.

Chemin: →(q ₀ )─1→(q ₁ )─0→(q ₂ )─1→(q ₀ )

avec cette nouvelle règle, le diagramme de transition devient comme suit:

Figure 3

ci-dessous dans chaque étape je choisis le nombre binaire suivant pour ajouter un bord manquant jusqu'à ce que je obtienne TD comme un 'Dfa complet'.

Step-4 : Six = 110.

Nous pouvons processus de '11' dans le présent TD dans la figure-3: →(q ₀ )─11→(q ₃ ) ─0→( ? ). Parce que 6 % 5 = 1 cela signifie ajouter une règle δ: (q ₃ , 0)→q ₁ .

Figure 4

Étape 5 : Sept = 111

┌──────┬──────┬─────────────┬─────────┬────────────┬───────────┐
│Number│Binary│Remainder(%5)│End-state│ Path       │ Add       │
├──────┼──────┼─────────────┼─────────┼────────────┼───────────┤
│Seven │111   │7 % 5 = 2    │q2       │ q0─11→q3│ q3─1→q2    │
└──────┴──────┴─────────────┴─────────┴────────────┴───────────┘

Figure 5

Étape-6 : Huit = 1000

┌──────┬──────┬─────────────┬─────────┬──────────┬─────────┐
│Number│Binary│Remainder(%5)│End-state│ Path     │ Add     │
├──────┼──────┼─────────────┼─────────┼──────────┼─────────┤
│Eight │1000  │8 % 5 = 3    │q3       │q0─100→q4 │ q4─0→q3  │
└──────┴──────┴─────────────┴─────────┴──────────┴─────────┘

Figure-6

Step-7 : Nine = 1001

┌──────┬──────┬─────────────┬─────────┬──────────┬─────────┐
│Number│Binary│Remainder(%5)│End-state│ Path     │ Add     │
├──────┼──────┼─────────────┼─────────┼──────────┼─────────┤
│Nine  │1001  │9 % 5 = 4    │q4       │q0─100→q4 │ q4─1→q4  │
└──────┴──────┴─────────────┴─────────┴──────────┴─────────┘

Figure-7

dans TD-7, total le nombre de bords est de 10 == Q × Σ = 5 × 2. Et c'est un DFA complet qui peut accepter toutes les chaînes binaires possibles dont l'équivalent décimal est divisible par 5.

Conception DFA accepter Ternaire nombre divisible par le nombre n:

Étape-1 identique à celle du binaire, utilisez la figure-1.

Étape-2 Ajouter Zéro, Un, Deux

┌───────┬───────┬─────────────┬─────────┬──────────────┐
│Decimal│Ternary│Remainder(%5)│End-state│   Add        │
├───────┼───────┼─────────────┼─────────┼──────────────┤
│Zero   │0      │0            │q0       │ δ:(q0,0)→q0  │
├───────┼───────┼─────────────┼─────────┼──────────────┤
│One    │1      │1            │q1       │ δ:(q0,1)→q1  │
├───────┼───────┼─────────────┼─────────┼──────────────┤
│Two    │2      │2            │q2       │ δ:(q0,2)→q3  │
└───────┴───────┴─────────────┴─────────┴──────────────┘

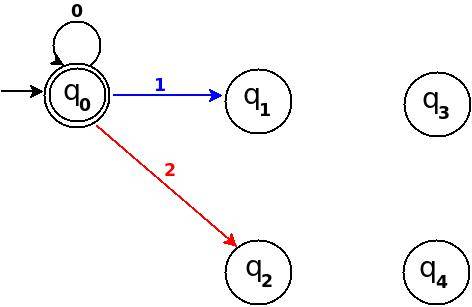
Figure 8

Étape 3 Ajouter Trois, Quatre, Cinq

┌───────┬───────┬─────────────┬─────────┬─────────────┐
│Decimal│Ternary│Remainder(%5)│End-state│  Add        │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Three  │10     │3            │q3       │ δ:(q1,0)→q3 │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Four   │11     │4            │q4       │ δ:(q1,1)→q4 │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Five   │12     │0            │q0       │ δ:(q1,2)→q0 │
└───────┴───────┴─────────────┴─────────┴─────────────┘

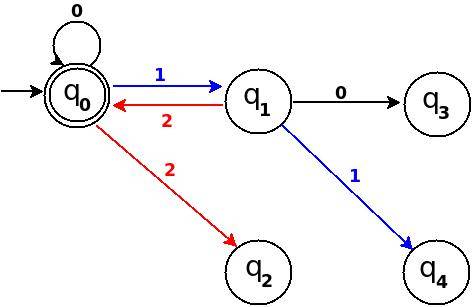
Figure 9

Étape-4 Ajouter Six, Sept, Huit

┌───────┬───────┬─────────────┬─────────┬─────────────┐
│Decimal│Ternary│Remainder(%5)│End-state│  Add        │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Six    │20     │1            │q1       │ δ:(q2,0)→q1 │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Seven  │21     │2            │q2       │ δ:(q2,1)→q2 │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Eight  │22     │3            │q3       │ δ:(q2,2)→q3 │
└───────┴───────┴─────────────┴─────────┴─────────────┘

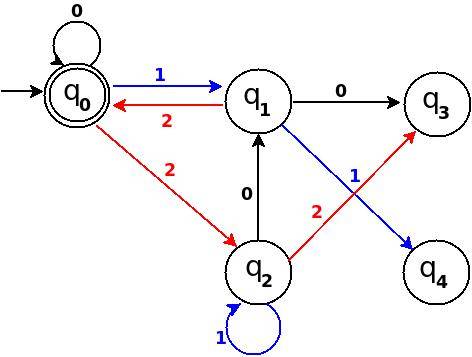
Figure-10

Étape 5 Ajouter De Neuf, Dix, Onze

┌───────┬───────┬─────────────┬─────────┬─────────────┐
│Decimal│Ternary│Remainder(%5)│End-state│  Add        │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Nine   │100    │4            │q4       │ δ:(q3,0)→q4 │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Ten    │101    │0            │q0       │ δ:(q3,1)→q0 │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Eleven │102    │1            │q1       │ δ:(q3,2)→q1 │
└───────┴───────┴─────────────┴─────────┴─────────────┘

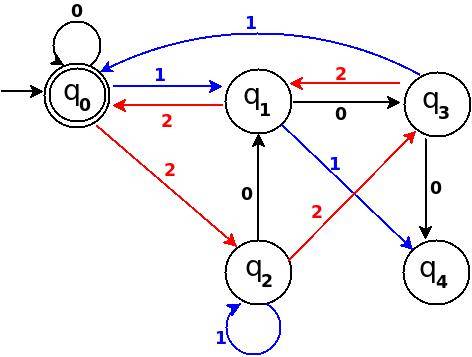
Figure 11

Étape-6 Ajouter Douze, Treize, Quatorze

┌────────┬───────┬─────────────┬─────────┬─────────────┐
│Decimal │Ternary│Remainder(%5)│End-state│  Add        │
├────────┼───────┼─────────────┼─────────┼─────────────┤
│Twelve  │110    │2            │q2       │ δ:(q4,0)→q2 │
├────────┼───────┼─────────────┼─────────┼─────────────┤
│Thirteen│111    │3            │q3       │ δ:(q4,1)→q3 │
├────────┼───────┼─────────────┼─────────┼─────────────┤
│Fourteen│112    │4            │q4       │ δ:(q4,2)→q4 │
└────────┴───────┴─────────────┴─────────┴─────────────┘

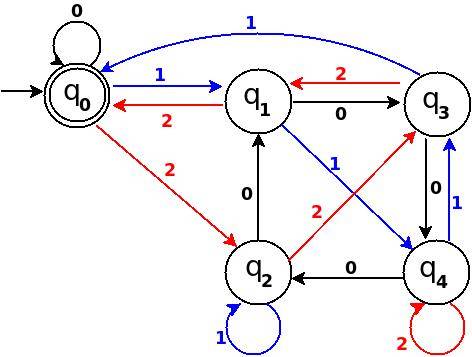
Figure-12

nombre Total de bords dans le diagramme de transition figure-12 sont 15 = Q × Σ = 5 * 3 (A Dfa complet). Et ce DFA peut accepter toutes les chaînes de caractères se composent de plus de {0, 1, 2} ceux équivalent décimal est divisible par 5.

Si vous remarquez à chaque étape, dans la table il y a trois entrées parce qu'à chaque étape j'ajoute tout bord sortant possible d'un État pour faire un DFA complet (et j'ajoute un bord de sorte que q _r l'état obtient pour le reste est r )!

pour ajouter, n'oubliez pas que l'union de deux langues régulières est aussi une régulière. Si vous avez besoin de concevoir un DFA qui accepte des chaînes binaires cet équivalent décimal est soit divisible par 3 ou 5, puis tirez deux Dfa séparés pour divisible par 3 et 5 puis union les deux DFA pour construire Dfa cible (pour 1 <= n <= 10 Votre avez à union 10 Dfa).

si on vous demande de dessiner DFA qui accepte des chaînes binaires telles que l'équivalent décimal est divisible par 5 et 3 à la fois, alors vous cherchez DFA divisible par 15 ( mais qu'en est-il de 6 et 8?).

Note: Dfa les ADF construits avec cette technique seront minimisés uniquement lorsqu'il y a Non facteur commun entre le nombre n et la base p. ex. il y a Non entre 5 et 2 dans le premier exemple, ou entre 5 et 3 dans le deuxième exemple, donc les ADF construits ci-dessus sont minimisés. Si vous êtes intéressé à lire plus au sujet de mini possibles États pour le nombre n et de base b lire papier: divisibilité et état La complexité .

^{ci-dessous, j'ai ajouté un script Python, je l'ai écrit pour le plaisir tout en apprenant la bibliothèque Python pygraphviz. Je l'ajoute, j'espère qu'il peut être utile pour quelqu'un dans un certain sens.}

la Conception de l'IFD pour la base " b "chaînes de nombre divisible par le nombre "n":

de sorte que nous pouvons appliquer ci-dessus truc pour attirer DFA pour reconnaître les chaînes de nombre dans n'importe quelle base 'b' ceux sont divisibles un donné le numéro de 'n' . En ce que DFA nombre total d'États sera n (pour n les restes) et le nombre de bords devrait être égal à 'b' * 'n' - qui est Dfa complète: 'b' = Nombre de symboles dans la langue de DFA et 'n' = nombre d'États.

en utilisant le truc ci-dessus, ci-dessous j'ai écrit un Script Python pour dessiner DFA pour l'entrée base et number . Dans script, la fonction divided_by_N popule les règles de transition de DFA dans base * number steps. Dans chaque pas-num, je convertis num en chaîne de nombre num_s en utilisant la fonction baseN() . Pour éviter de traiter chaque chaîne de nombres, j'ai utilisé une structure de données temporaire lookup_table . À chaque étape, l'état final de la chaîne de caractères num_s est évalué et stocké dans lookup_table à utiliser à l'étape suivante.

pour le graphique de transition de DFA, j'ai écrit une fonction draw_transition_graph en utilisant Bibliothèque Pygraphviz (très facile à utiliser). Pour utiliser ce script, vous devez installer graphviz . Pour ajouter des bords colorés dans le diagramme de transition, je génère au hasard des codes de couleur pour chaque symbole get_color_dict fonction.

#!/usr/bin/env python
import pygraphviz as pgv
from pprint import pprint
from random import choice as rchoice

def baseN(n, b, syms="0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"):
    """ converts a number `n` into base `b` string """
    return ((n == 0) and syms[0]) or (
        baseN(n//b, b, syms).lstrip(syms[0]) + syms[n % b])

def divided_by_N(number, base):
    """
    constructs DFA that accepts given `base` number strings
    those are divisible by a given `number`
    """
    ACCEPTING_STATE = START_STATE = '0'
    SYMBOL_0 = '0'
    dfa = {
        str(from_state): {
            str(symbol): 'to_state' for symbol in range(base)
        }
        for from_state in range(number)
    }
    dfa[START_STATE][SYMBOL_0] = ACCEPTING_STATE
    # `lookup_table` keeps track: 'number string' -->[dfa]--> 'end_state'
    lookup_table = { SYMBOL_0: ACCEPTING_STATE }.setdefault
    for num in range(number * base):
        end_state = str(num % number)
        num_s = baseN(num, base)
        before_end_state = lookup_table(num_s[:-1], START_STATE)
        dfa[before_end_state][num_s[-1]] = end_state
        lookup_table(num_s, end_state)
    return dfa

def symcolrhexcodes(symbols):
    """
    returns dict of color codes mapped with alphabets symbol in symbols
    """
    return {
        symbol: '#'+''.join([
            rchoice("8A6C2B590D1F4E37") for _ in "FFFFFF"
        ])
        for symbol in symbols
    }

def draw_transition_graph(dfa, filename="filename"):
    ACCEPTING_STATE = START_STATE = '0'
    colors = symcolrhexcodes(dfa[START_STATE].keys())
    # draw transition graph
    tg = pgv.AGraph(strict=False, directed=True, decorate=True)
    for from_state in dfa:
        for symbol, to_state in dfa[from_state].iteritems():
            tg.add_edge("Q%s"%from_state, "Q%s"%to_state,
                        label=symbol, color=colors[symbol],
                        fontcolor=colors[symbol])

    # add intial edge from an invisible node!
    tg.add_node('null', shape='plaintext', label='start')
    tg.add_edge('null', "Q%s"%START_STATE,)

    # make end acception state as 'doublecircle'
    tg.get_node("Q%s"%ACCEPTING_STATE).attr['shape'] = 'doublecircle'
    tg.draw(filename, prog='circo')
    tg.close()

def print_transition_table(dfa):
    print("DFA accepting number string in base '%(base)s' "
            "those are divisible by '%(number)s':" % {
                'base': len(dfa['0']),
                'number': len(dfa),})
    pprint(dfa)

if __name__ == "__main__":
    number = input ("Enter NUMBER: ")
    base = input ("Enter BASE of number system: ")
    dfa = divided_by_N(number, base)

    print_transition_table(dfa)
    draw_transition_graph(dfa)

de l'Exécuter:

~/study/divide-5/script$ python script.py 
Enter NUMBER: 5
Enter BASE of number system: 4
DFA accepting number string in base '4' those are divisible by '5':
{'0': {'0': '0', '1': '1', '2': '2', '3': '3'},
 '1': {'0': '4', '1': '0', '2': '1', '3': '2'},
 '2': {'0': '3', '1': '4', '2': '0', '3': '1'},
 '3': {'0': '2', '1': '3', '2': '4', '3': '0'},
 '4': {'0': '1', '1': '2', '2': '3', '3': '4'}}
~/study/divide-5/script$ ls
script.py filename.png
~/study/divide-5/script$ display filename

sortie:

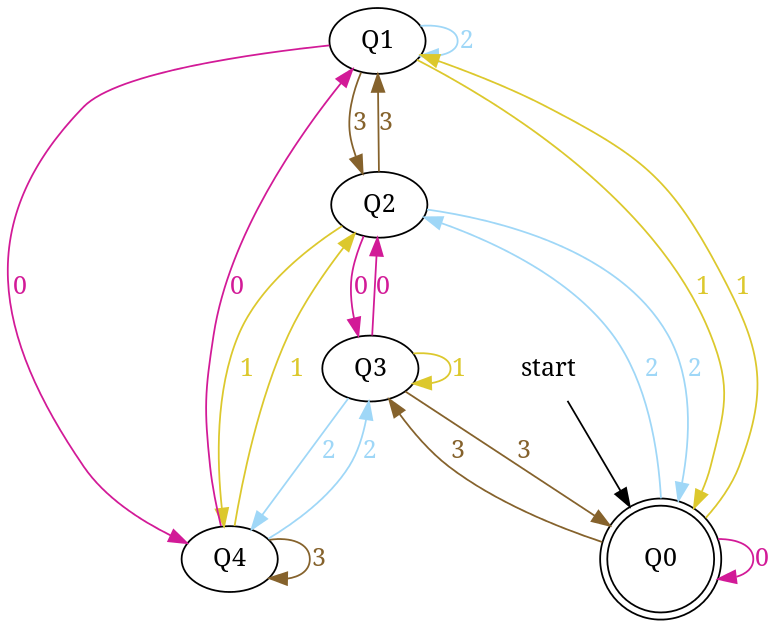
DFA acceptant nombre de chaînes dans la base de 4 personnes sont divisibles par 5

de même, entrer base = 4 et nombre = 7 pour générer - dfa accepting number string in base '4' those are divisible par '7'

Btw, essayez de changer filename en .png ou .jpeg .

<sub>Références celles que j'utilise pour écrire ce script:

➊ La Fonction baseN à partir de "convertir un entier en une chaîne de caractères en une donnée numérique de base en python"

"Python does not see pygraphviz "

"Python-FSM "

Pour générer des codes de couleur hexadécimaux aléatoires pour chaque symbole de langue: " Comment ferais-je un générateur de code aléatoire hexdigit .rejoindre et pour les boucles?"</sub>