création d'une" carte radar " (A. K. A. graphique d'étoiles; graphique d'Araignée) utilisant ggplot2 en R

D'abord, nous chargeons quelques paquets.

library(reshape2)
library(ggplot2)
library(scales)

Voici les données de l'exemple radarchart auquel vous avez fait référence.

maxmin <- data.frame(
  total  = c(5, 1),
  phys   = c(15, 3),
  psycho = c(3, 0),
  social = c(5, 1),
  env    = c(5, 1)
)
dat <- data.frame(
  total  = runif(3, 1, 5),
  phys   = rnorm(3, 10, 2),
  psycho = c(0.5, NA, 3),
  social = runif(3, 1, 5),
  env    = c(5, 2.5, 4)
)

nous avons besoin d'un peu de manipulation pour les rendre appropriés pour ggplot.

les normaliser, ajouter une colonne id et convertir en format long.

normalised_dat <- as.data.frame(mapply(
    function(x, mm)
    {
      (x - mm[2]) / (mm[1] - mm[2])
    },
    dat,
    maxmin
))

normalised_dat$id <- factor(seq_len(nrow(normalised_dat)))
long_dat <- melt(normalised_dat, id.vars = "id")

ggplot enveloppe également les valeurs de sorte que le premier et le dernier facteurs se rencontrent. Nous ajoutons un niveau de facteur supplémentaire pour éviter cela. Ce n'est plus vrai.

(long_dat$variable) <- c(niveaux(long_dat$variable), "")

Voici l'intrigue. Ce n'est pas tout à fait la même chose, mais ça devrait vous aider à commencer.

ggplot(long_dat, aes(x = variable, y = value, colour = id, group = id)) +
  geom_line() +
  coord_polar(theta = "x", direction = -1) +
  scale_y_continuous(labels = percent)

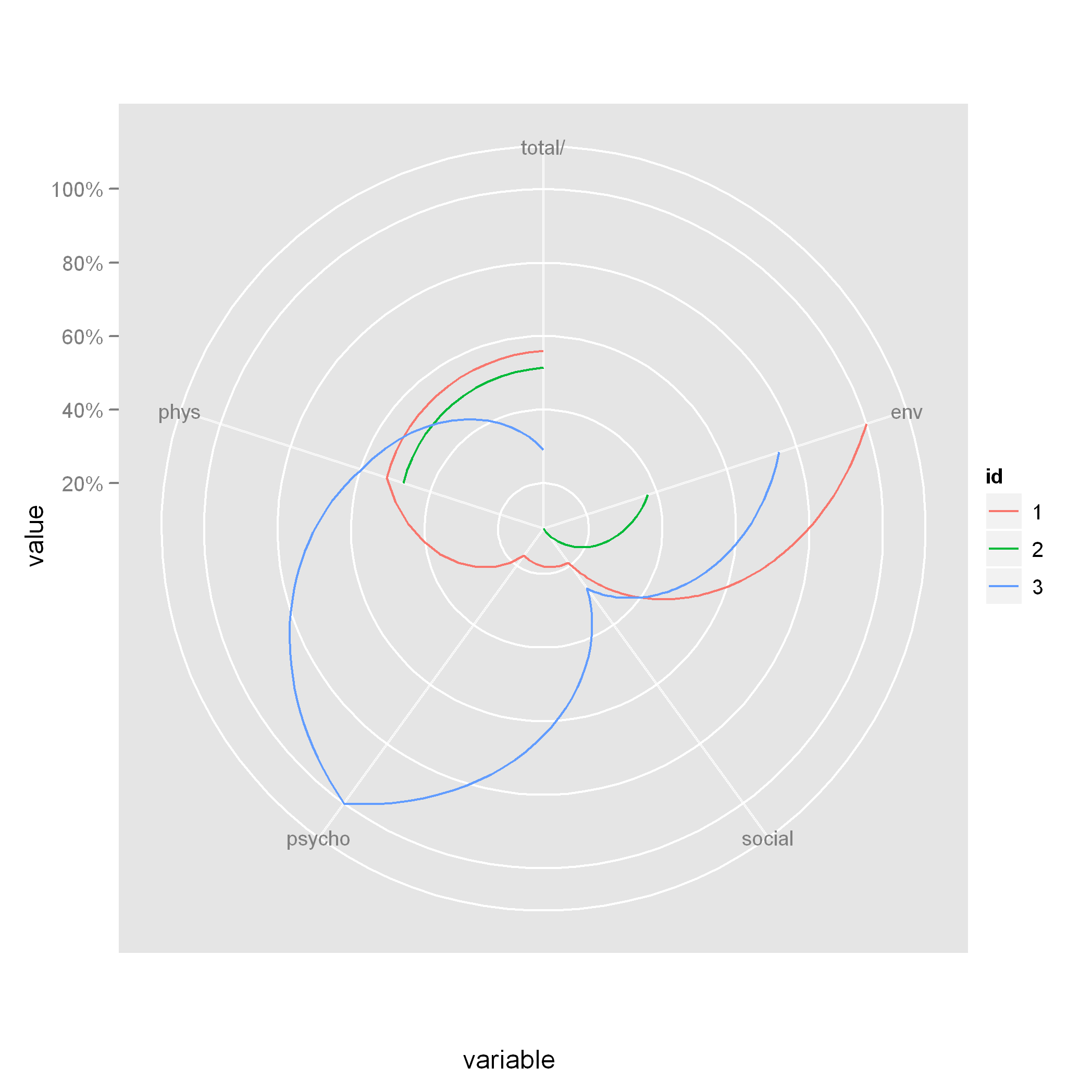Notez que lorsque vous utilisez coord_polar , les lignes sont courbes. Si vous voulez des lignes droites, alors vous devrez essayer une autre technique.

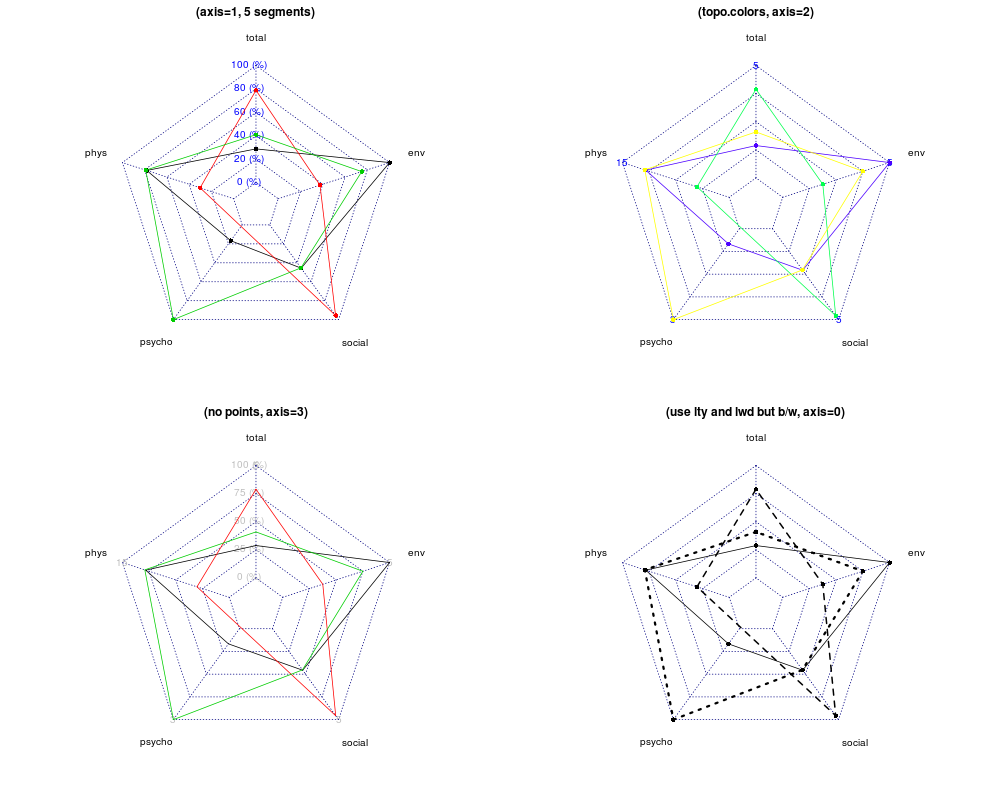
si vous cherchez une version non polar coordonnée, je pense que la fonction suivante vous aidera:

###################################
##Radar Plot Code
##########################################
##Assumes d is in the form:
# seg  meanAcc sdAcc   meanAccz sdAccz meanSpd   sdSpd   cluster
# 388  -0.038   1.438   -0.571  0.832  -0.825   0.095       1
##where seg is the individual instance identifier
##cluster is the cluster membership
##and the variables from meanACC to sdSpd are used for the clustering
##and thus should be individual lines on the radar plot
radarFix = function(d){
  ##assuming the passed in data frame 
  ##includes only variables you would like plotted and segment label
  d$seg=as.factor(d$seg)
  ##find increment
  angles = seq(from=0, to=2*pi, by=(2*pi)/(ncol(d)-2))
  ##create graph data frame
  graphData= data.frame(seg="", x=0,y=0)
  graphData=graphData[-1,]



  for(i in levels(d$seg)){
    segData= subset(d, seg==i)
    for(j in c(2:(ncol(d)-1))){
      ##set minimum value such that it occurs at 0. (center the data at -3 sd)
      segData[,j]= segData[,j]+3

      graphData=rbind(graphData, data.frame(seg=i, 
                                            x=segData[,j]*cos(angles[j-1]),
                                            y=segData[,j]*sin(angles[j-1])))
    }
    ##completes the connection
    graphData=rbind(graphData, data.frame(seg=i, 
                                          x=segData[,2]*cos(angles[1]),
                                          y=segData[,2]*sin(angles[1])))

  }
  graphData

}

si vous traquez par groupe ou groupe, vous pouvez alors utiliser ce qui suit:

radarData = ddply(clustData, .(cluster), radarFix)
ggplot(radarData, aes(x=x, y=y, group=seg))+
  geom_path(alpha=0.5,colour="black")+
  geom_point(alpha=0.2, colour="blue")+
  facet_wrap(~cluster)

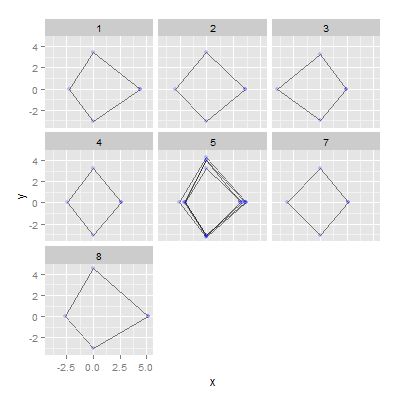
cela devrait fonctionner avec l'échantillon de données suivant:

   seg  meanAccVs sdAccVs meanSpd sdSpd cluster
  1470     1.420   0.433  -0.801 0.083       1
  1967    -0.593   0.292   1.047 0.000       3
  2167    -0.329   0.221   0.068 0.053       7
  2292    -0.356   0.214  -0.588 0.056       4
  2744     0.653   1.041  -1.039 0.108       5
  3448     2.189   1.552  -0.339 0.057       8
  7434     0.300   0.250  -1.009 0.088       5
  7764     0.607   0.469  -0.035 0.078       2
  7942     0.124   1.017  -0.940 0.138       5
  9388     0.742   1.289  -0.477 0.301       5

j'ai passé plusieurs jours sur ce problème et à la fin j'ai décidé de construire mon propre paquet au sommet de ggradar . Le noyau est une version améliorée de la fonction de @Tony M.:

CalculateGroupPath4 <- function(df) {
   angles = seq(from=0, to=2*pi, by=(2*pi)/(ncol(df)-1)) # find increment
   xx<-c(rbind(t(plot.data.offset[,-1])*sin(angles[-ncol(df)]),
               t(plot.data.offset[,2])*sin(angles[1])))
   yy<-c(rbind(t(plot.data.offset[,-1])*cos(angles[-ncol(df)]), 
               t(plot.data.offset[,2])*cos(angles[1])))
  graphData<-data.frame(group=rep(df[,1],each=ncol(df)),x=(xx),y=(yy))
  return(graphData)
}
CalculateGroupPath5 <- function(mydf) {
   df<-cbind(mydf[,-1],mydf[,2])
   myvec<-c(t(df))
   angles = seq(from=0, to=2*pi, by=(2*pi)/(ncol(df)-1)) # find increment
   xx<-myvec*sin(rep(c(angles[-ncol(df)],angles[1]),nrow(df)))
   yy<-myvec*cos(rep(c(angles[-ncol(df)],angles[1]),nrow(df)))
   graphData<-data.frame(group=rep(mydf[,1],each=ncol(mydf)),x=(xx),y=(yy))
   return(graphData)
}

microbenchmark::microbenchmark(CalculateGroupPath(plot.data.offset),
                              CalculateGroupPath4(plot.data.offset),
                              CalculateGroupPath5(plot.data.offset), times=1000L)
Unit: microseconds
expr       min         lq       mean     median         uq      max neval
CalculateGroupPath(plot.data.offset) 20768.163 21636.8715 23125.1762 22394.1955 23946.5875 86926.97  1000
CalculateGroupPath4(plot.data.offset)   550.148   614.7620   707.2645   650.2490   687.5815 15756.53  1000
CalculateGroupPath5(plot.data.offset)   577.634   650.0435   738.7701   684.0945   726.9660 11228.58  1000

noter que j'ai effectivement comparé plus de fonctions dans ce benchmark - entre autres fonctions de ggradar . Généralement la solution de @Tony M est bien écrite - dans le sens de la logique et que vous pouvez l'utiliser dans beaucoup d'autres langues, comme par exemple Javascript, avec quelques modifications. Cependant R devient beaucoup plus rapide si vous vectorisez les opérations. Par conséquent, le gain massif de temps de calcul avec ma solution.

toutes les réponses sauf @Tony M. ont utilisé la fonction coord_polar - de ggplot2 . Il y a quatre avantages à rester dans le système de coordonnées cartésien:

1. il vous permet de transporter votre solution aussi à d'autres indiquer les colis, par exemple plotly .
2. toute personne qui a une certaine compréhension de la norme cosinus et sinus-fonction peut comprendre comment la transformation des données fonctionne.
3. Vous pouvez étendre et de personnaliser l'intrigue comme vous voulez - l'enfer, vous pouvez l'utiliser avec n'importe quel tracé paquet disponible dans R!
4. vous n'avez pas besoin de charger any excepté votre paquet de pointage. Toutefois, il est généralement logique de réévaluer vos données, par exemple avec le paquet scales de Hadley.

si comme moi vous ne savez rien sur la façon de faire des tracés radar quand vous trouvez ce fil de discussion : le coord_polar() pourrait créer de bons tracés radar. Toutefois, la mise en œuvre est quelque peu délicate. Quand je l'ai essayé, j'ai eu plusieurs problèmes:

1. le premier numéro avec cette approche est que les lignes ne doivent pas rester droit.
2. le coord_polar() ne se traduit pas, par exemple, en plotly.
3. le système de coordonnées polaires rend la personnalisation détaillée difficile, parce que les annotations et autres caractéristiques seront également jetées dans les coordonnées polaires.

ce gars-là a fait un belle carte radar en utilisant coord_polar .

Cependant compte tenu de mon expériences - je conseille plutôt de ne pas utiliser le coord_polar() -truc. Au lieu de cela, si vous êtes à la recherche d'un 'moyen facile' de créer un ggplot-radar statique, peut-être utiliser le grand ggforce - paquet pour dessiner des cercles du radar. Pas de garantie que ce soit plus facile que d'utiliser mon package, mais de l'adaptilité semble plus approprié que coord_polar . L'inconvénient est que par exemple plotly ne supporte pas l'extension ggforce.

EDIT: maintenant j'ai trouvé un bel exemple avec ggplot2 coordin_polar qui a révisé un peu mon opinion.

Voici une réponse qui le fait presque en ggplot.

Je ne revendique rien de plus que de mettre l'exemple ici, il est basé sur ce que Hadley a montré ici https://github.com/hadley/ggplot2/issues/516

Tout ce que j'ai fait était d'utiliser depleer / tidyr à la place et de choisir seulement 3 voitures pour la simplicité

les questions encore en suspens sont 1) le dernier et le premier point ne sont pas connectés, c'est évident, si vous voyez le coordin_polar comme un enveloppement de l'axe x traditionnel. Il n'ya aucune raison pourquoi ils devraient être connecté. Mais c'est ainsi que les cartes radar sont normalement affichées 2) pour ce faire, vous devez ajouter un segment manuellement entre ces 2 points. Un peu de manipulation et quelques couches supplémentaires devraient le faire. Je vais essayer de travailler sur elle si j'ai le temps

library(dplyr);library(tidyr);library(ggplot2)
#make some data
data = mtcars[c(27,19,16),]
data$model=row.names(data)

#connvert data to long format and also rescale it into 0-1 scales
data1 <- data %>% gather(measure,value,-model) %>% group_by(measure) %>% mutate(value1=(value-min(value))/(max(value)-min(value)))

is.linear.polar <- function(coord) TRUE
ggplot(data1,aes(x=measure,y=value1,color=model,group=model))+geom_line()+coord_polar()