Conversion d'une expression numérique python en LaTeX

Voici une méthode assez longue mais encore incomplète qui n'implique pas sympy en aucune façon. C'est assez pour couvrir l'exemple de (-b-sqrt(b**2-4*a*c))/(2*a) qui est traduit en \frac{- b - \sqrt{b^{2} - 4 \; a \; c}}{2 \; a} et rend comme

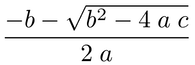
il crée essentiellement le AST et le parcourt en produisant le latex math qui correspond aux noeuds AST. Ce qui est là devrait donner assez d'idée de la façon de l'étendre dans les endroits où il manque.

import ast

class LatexVisitor(ast.NodeVisitor):

    def prec(self, n):
        return getattr(self, 'prec_'+n.__class__.__name__, getattr(self, 'generic_prec'))(n)

    def visit_Call(self, n):
        func = self.visit(n.func)
        args = ', '.join(map(self.visit, n.args))
        if func == 'sqrt':
            return '\sqrt{%s}' % args
        else:
            return r'\operatorname{%s}\left(%s\right)' % (func, args)

    def prec_Call(self, n):
        return 1000

    def visit_Name(self, n):
        return n.id

    def prec_Name(self, n):
        return 1000

    def visit_UnaryOp(self, n):
        if self.prec(n.op) > self.prec(n.operand):
            return r'%s \left(%s\right)' % (self.visit(n.op), self.visit(n.operand))
        else:
            return r'%s %s' % (self.visit(n.op), self.visit(n.operand))

    def prec_UnaryOp(self, n):
        return self.prec(n.op)

    def visit_BinOp(self, n):
        if self.prec(n.op) > self.prec(n.left):
            left = r'\left(%s\right)' % self.visit(n.left)
        else:
            left = self.visit(n.left)
        if self.prec(n.op) > self.prec(n.right):
            right = r'\left(%s\right)' % self.visit(n.right)
        else:
            right = self.visit(n.right)
        if isinstance(n.op, ast.Div):
            return r'\frac{%s}{%s}' % (self.visit(n.left), self.visit(n.right))
        elif isinstance(n.op, ast.FloorDiv):
            return r'\left\lfloor\frac{%s}{%s}\right\rfloor' % (self.visit(n.left), self.visit(n.right))
        elif isinstance(n.op, ast.Pow):
            return r'%s^{%s}' % (left, self.visit(n.right))
        else:
            return r'%s %s %s' % (left, self.visit(n.op), right)

    def prec_BinOp(self, n):
        return self.prec(n.op)

    def visit_Sub(self, n):
        return '-'

    def prec_Sub(self, n):
        return 300

    def visit_Add(self, n):
        return '+'

    def prec_Add(self, n):
        return 300

    def visit_Mult(self, n):
        return '\;'

    def prec_Mult(self, n):
        return 400

    def visit_Mod(self, n):
        return '\bmod'

    def prec_Mod(self, n):
        return 500

    def prec_Pow(self, n):
        return 700

    def prec_Div(self, n):
        return 400

    def prec_FloorDiv(self, n):
        return 400

    def visit_LShift(self, n):
        return '\operatorname{shiftLeft}'

    def visit_RShift(self, n):
        return '\operatorname{shiftRight}'

    def visit_BitOr(self, n):
        return '\operatorname{or}'

    def visit_BitXor(self, n):
        return '\operatorname{xor}'

    def visit_BitAnd(self, n):
        return '\operatorname{and}'

    def visit_Invert(self, n):
        return '\operatorname{invert}'

    def prec_Invert(self, n):
        return 800

    def visit_Not(self, n):
        return '\neg'

    def prec_Not(self, n):
        return 800

    def visit_UAdd(self, n):
        return '+'

    def prec_UAdd(self, n):
        return 800

    def visit_USub(self, n):
        return '-'

    def prec_USub(self, n):
        return 800
    def visit_Num(self, n):
        return str(n.n)

    def prec_Num(self, n):
        return 1000

    def generic_visit(self, n):
        if isinstance(n, ast.AST):
            return r'' % (n.__class__.__name__, ', '.join(map(self.visit, [getattr(n, f) for f in n._fields])))
        else:
            return str(n)

    def generic_prec(self, n):
        return 0

def py2tex(expr):
    pt = ast.parse(expr)
    return LatexVisitor().visit(pt.body[0].value)

vous pouvez utiliser SymPy. Il suffit de passer la chaîne à l' sympify() fonction d'abord, qui la convertira en une expression SymPy valide (c'est-à-dire créer les symboles pour vous, etc.). Donc, vous pourriez faire

>>> latex(sympify('1+2**(x+y)'))
1 + 2^{x + y}

S() est aussi un raccourci pour sympify(), i.e.,latex(S('1+2**(x+y)')) fonctionne également.

Juste un petit correctif à Geoff Reedy excellente réponse:

class GenerateSymbols(defaultdict):
    def __missing__(self, key):
        self[key] = sympy.Symbol(key)
        return self[key]

avant de ne pas ajouter le nouvel article au dict. Maintenant, vous pouvez l'utiliser avec votre expression:

d= GenerateSymbols()    
eq = '(-b-sqrt(b**2-4*a*c))/(2*a)'

et vous pouvez simplifier un peu avant de le convertir au LaTeX:

sympy.latex(sympy.simplify(eval(eq,d)))

et vous obtenez ceci:

'$- \frac{b + \operatorname{sqrt}\left(- 4 a c + b^{2}\right)}{2 a}$'

pour construire sur la réponse de tom10 vous pouvez définir un dictionnaire qui générera des symboles et l'utiliser lors de l'appel eval:

from collections import defaultdict
class GenerateSymbols(defaultdict):
  def __missing__(self, key):
    return sympy.Symbol(key)

alors si vous utilisez

sympy.latex(eval('1+2**(x+y)',GenerateSymbols()))

vous ne devriez pas avoir à vous soucier de pré-créer des symboles pour les variables.