Temps Amorti Constant

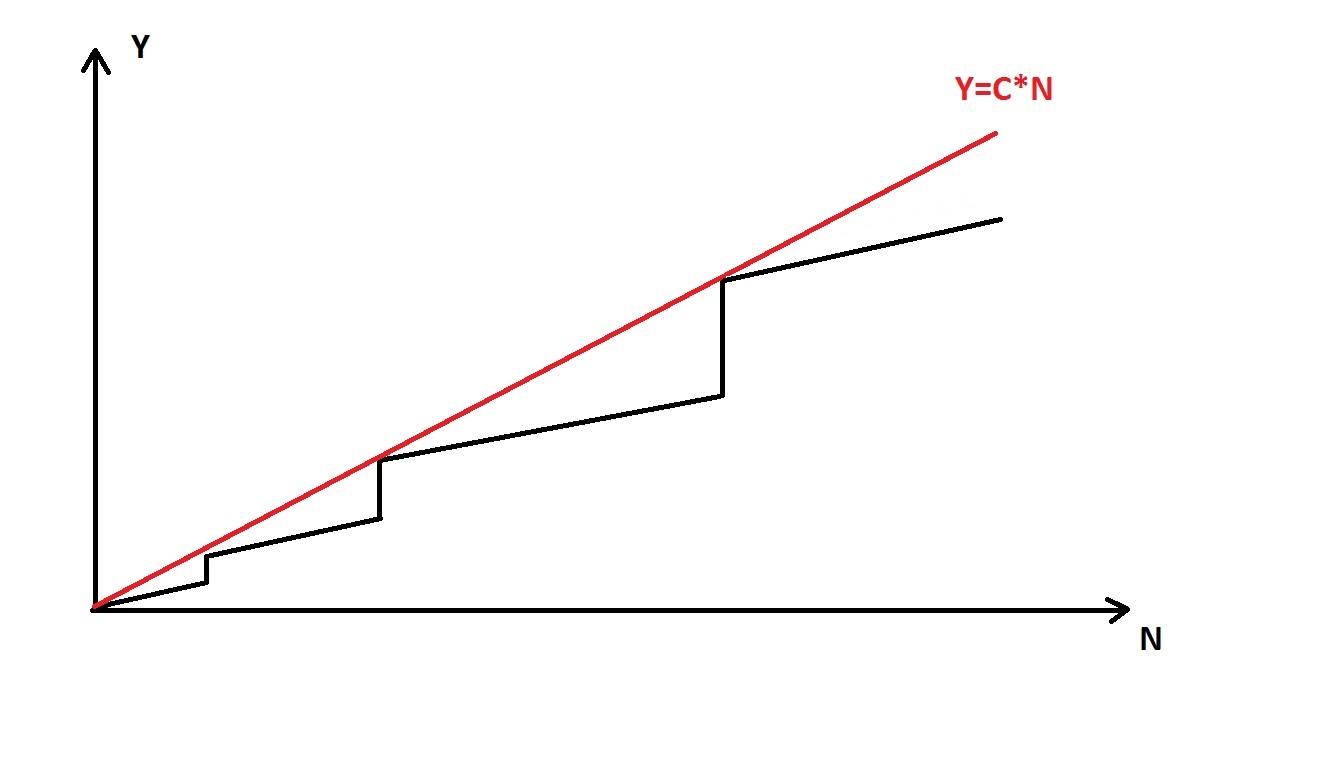
pour développer une façon intuitive de penser à ce sujet, envisager l'insertion d'éléments dans dynamic array (par exemple std::vector en C++). Traçons un graphique, qui montre la dépendance du nombre d'opérations (Y) nécessaires pour insérer N éléments dans le tableau:

les parties verticales du graphe noir correspondent à des réallocations de mémoire afin d'étendre un tableau. Ici, nous peut voir que cette dépendance peut être grossièrement représentée par une ligne. Et cette équation linéaire est Y=C*N + b ( C est constant, b = 0 dans notre cas). Par conséquent, nous pouvons dire que nous avons besoin de passer C*N opérations en moyenne pour ajouter N éléments à tableau, ou C*1 opérations pour ajouter un élément (temps constant amorti).

j'ai trouvé ci-dessous L'explication de Wikipedia utile, après avoir répété la lecture pendant 3 fois:

Source: https://en.wikipedia.org/wiki/Amortized_analysis#Dynamic_Array

"Tableau Dynamique

Amorti Analyse de l'opération Push pour un Tableau Dynamique

considère un tableau dynamique qui croît en taille que plus d'éléments sont ajoutés à elle comme un Liste de tableaux en Java. Si nous avons commencé avec un tableau dynamique de taille 4, Il faudrait un temps constant pour pousser quatre éléments dessus. Pourtant, pousser un cinquième élément sur ce tableau prendrait plus de temps que le tableau devrait créer un nouveau tableau de double la taille actuelle (8), copie les éléments anciens sur le nouveau tableau, puis ajouter la nouvelle élément. De même, les trois opérations de poussée suivantes seraient constantes: temps, et puis l'ajout ultérieur exigerait un autre lent doublement de la taille de la matrice.

en général si nous considérons un nombre arbitraire de Push n à un tableau de taille n, on remarque que les opérations de poussée prennent du temps constant sauf pour le dernier qui prend O(n) le temps d'effectuer la taille de doubler opération. Puisqu'il y avait n opérations total nous pouvons prendre la moyenne de cela et de trouver que pour pousser des éléments sur le tableau dynamique prend: O(n/n)=O(1), de la constante de temps."

à mon sens comme un histoire simple:

suppose que tu as beaucoup d'argent. Et tu veux les empiler dans une pièce. Et, vous avez de longs bras et de jambes, autant longtemps que vous avez besoin maintenant ou dans l'avenir. Et, vous devez remplir tout dans une pièce, il est donc facile de la verrouiller.

donc, vous allez à droite à la fin/ coin de la salle et commencer à les empiler. En les empilant, la pièce s'épuisera lentement. Cependant, comme vous remplissez il était facile de les empiler. Obtenu l'argent, mettre de l'argent. Facile. Il est O(1). Nous n'avons pas besoin de déplacer les précédents de l'argent.

une fois que la pièce manque d'espace. Il nous faut une autre chambre, qui est plus grande. Ici, il y a un problème, puisque nous ne pouvons avoir qu'une seule pièce de sorte que nous ne pouvons avoir qu'une seule serrure, nous devons déplacer tout l'argent existant dans cette pièce dans la nouvelle plus grande pièce. Donc, déplacer tout l'argent, de la petite pièce, à la plus grande pièce. C'est, pile tous les à nouveau. Donc, nous avons besoin de déplacer tout l'argent précédent. Il est donc O(N). (en supposant que N est le nombre total de monnaie de la monnaie précédente)

en d'autres termes, il était facile jusqu'À N, seulement 1 opération, mais quand nous avons besoin de passer à une plus grande salle, Nous avons fait N opérations. Donc, en d'autres termes, si nous faisons la moyenne, il est 1 insert dans le début, et 1 mouvement de plus tout en se déplaçant à une autre pièce. Total de 2 Opérations, un insert, un mouvement.

en supposant que N est grand comme 1 million même dans la petite salle, les 2 opérations par rapport à N (1 million) n'est pas vraiment un nombre comparable, de sorte qu'il est considéré constant ou O (1).

en supposant que lorsque nous faisons tout ce qui précède dans une autre plus grande salle, et encore besoin de se déplacer. C'est toujours le même. dire, N2 (disons 1 milliard de dollars) est le nouveau montant de compter de l'argent dans la plus grande pièce

donc, nous avons N2 (qui comprend N du précédent puisque nous passons tous de la petite à la plus grande pièce)

nous avons encore besoin de seulement 2 Opérations, une est insérée dans une plus grande salle, puis une autre opération de déplacement pour passer à un pair chambre plus grande.

donc, même pour N2 (1 milliard), il est de 2 opérations pour chacun. qui n'est rien de nouveau. Donc, il est constant, ou O(1)

ainsi, comme le N augmente de N à N2, ou autre, il n'importe pas beaucoup. Il est encore constant, ou o(1) opérations requises pour chacun des N.

---

supposons maintenant, vous avez N Comme 1, très petit, le compte de l'argent est petit, et vous avez une très petite chambre, qui s'adaptera seulement 1 compter de l'argent.

dès Que vous remplissez l'argent dans la chambre, la salle est remplie.

quand vous allez à la plus grande salle, supposez qu'il ne peut contenir qu'un seul argent de plus, total de 2 compte d'argent. Cela signifie que le précédent a déplacé de l'argent et 1 de plus. Et encore, il est rempli.

de cette façon, le N croît lentement, et il n'est pas plus constant O(1), puisque nous déplaçons tout l'argent de la salle précédente, mais ne peut tenir que 1 argent de plus.

après 100 fois, la nouvelle chambre s'adapte 100 Compte d'argent de la précédente et 1 argent de plus il peut accueillir. C'est O(N), puisque O(N+1) est O(N), c'est-à-dire que le degré de 100 ou 101 est le même, les deux sont des centaines, par opposition à l'histoire précédente de, un à des millions et un à des milliards.

donc, c'est une façon inefficace d'allouer des pièces (ou mémoire vive) pour notre argent (variables).

---

donc, une bonne façon est allouer plus de place, avec des puissances de 2.

1er la taille de la pièce = correspond à 1 chef d'accusation d'argent

2ème chambre de taille = fits 4 nombre de l'argent

3ème chambre size = correspond à 8 compter de l'argent

Taille de la 4e chambre = taille 16 compte d'argent

5e taille de la chambre = correspond à 32 nombre de l'argent

6 taille de la chambre = correspond à 64 compter de l'argent

7ème dimension de la chambre = ajustement 128 compte d'argent

8ème taille de chambre = taille 256 compte d'argent

9 taille de la chambre = fits 512 count de l'argent

10 taille de la chambre= correspond à 1024 compter de l'argent

11 taille de la chambre= correspond à 2 048 compter de l'argent

...

16 taille de la chambre= fits de 65 536 compter de l'argent

...

Taille de la 32e chambre= taille de la chambre 4 294 967 296 compte d'argent

...

64e taille de la chambre= fits 18,446,744,073,709,551,616 compter de l'argent

Pourquoi est-ce mieux? Parce qu'il semble se développer lentement au début, et plus vite plus tard, c'est-à-dire par rapport à la quantité de mémoire dans notre mémoire vive.

cela est utile parce que, dans le premier cas bien qu'il soit bon, la quantité totale de travail à faire par argent est fixe (2) et non comparable à la taille de la pièce (N), la pièce que nous avons pris dans les étapes initiales pourraient être trop grandes (1 million) que nous ne pouvons pas utiliser pleinement en fonction de si nous pouvons obtenir que beaucoup d'argent à économiser du tout dans le premier cas.

cependant, dans le dernier cas, les pouvoirs de 2, il se développe dans les limites de notre RAM. Et donc, en augmentant en puissance de 2, l'analyse Armotized reste constante et il est amical pour le RAM limité que nous avons à ce jour.

Les explications ci-dessus s'appliquent à l'Analyse Agrégée, l'idée de prendre "une moyenne" sur plusieurs opérations. Je ne suis pas sûr comment ils appliquent aux banquiers-méthode ou les physiciens méthodes D'analyse amortie.

maintenant. Je ne suis pas exactement sûr de la réponse correcte. Mais cela aurait à voir avec la condition principale des deux physiciens+méthodes de Banquier:

(somme des éléments amortis-coût d'exploitation) > = (somme des éléments réels-coût d'exploitation).

la principale difficulté à laquelle je suis confronté est que, étant donné que les coûts D'exploitation amortis-asymptotiques diffèrent des coûts normaux-asymptotiques -, Je ne sais pas comment évaluer l'importance des coûts amortis.

C'est-à-dire quand quelqu'un me donne un coût amorti, je sais que ce n'est pas le même que le coût normal-asymptotique quelles conclusions dois-je tirer du coût amorti alors?

depuis que nous avons le cas de certaines opérations étant surfacturé tandis que d'autres opérations sont sous-facturées, une hypothèse pourrait être que la cotation amortie-coûts des opérations individuelles serait sans signification.

pour par exemple: pour un tas de fibonacci, en indiquant le coût amorti de juste décroissant-clé à être O (1) est dénué de sens puisque les coûts sont réduits par "le travail fait par les opérations plus tôt dans le potentiel croissant du tas."

ou

nous pourrions avoir une autre hypothèse que les raisons sur les coûts amortis comme suit:

1. je sais que l'opération coûteuse va être précédée par de multiples opérations à faible coût.

2. pour des raisons d'analyse, je vais surcharger certaines opérations à faible coût, de sorte que leur coût asymptotique ne CHANGE pas.

3. avec ces opérations bon marché, je peux prouver que L'opération coûteuse a un plus petit asymptotique COÛT.

4. ainsi j'ai amélioré/diminué la limite asymptotique du coût des opérations N.

ainsi amorti-analyse des coûts + amorti-limites des coûts sont maintenant applicables uniquement aux opérations coûteuses. Les opérations bon marché ont le même coût asymptotique-amorti-comme leur coût normal-asymptotique -.