Heuristiques cohérentes et admissibles

comme Russel et Norvig le font remarquer dans Intelligence Artificielle: Une Approche Moderne (le manuel D'IA le plus couramment utilisé) il est difficile de trouver un heuristique qui est admissible mais qui n'est pas cohérent.

évidemment, vous pouvez sélectionner des valeurs pour les noeuds dans un graphique tel que l'heuristique qu'ils représentent est admissible mais pas cohérente. Ce document par Felner et al a un bon exemple des deux façons que cela est possible, mais c'est un peu dense, donc je vais résumer:

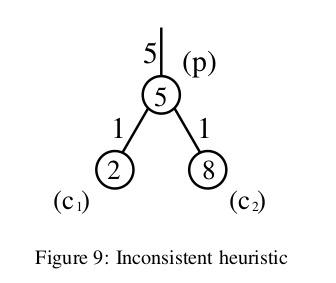
• cette heuristique est incohérente à c1 parce qu'il donne une limite inférieure (c.-à-d. moins informative) sur le coût pour atteindre le but que son noeud parent est. Le coût estimé pour atteindre le but à travers le noeud parent est d'au moins 10 (parce que le coût du chemin vers p est 5 et l'estimation heuristique p est également à 5). L'estimation des coûts pour atteindre le but par c1, cependant, est seulement 8 (coût du parent (5), plus coût du chemin du parent (1), plus estimation heuristique à c1 (2)).
• puisque ce graphique n'est pas dirigé, cette heuristique est également incohérente à c2, parce qu'à partir de c2p a le même problème que ci-dessus.

Felner et coll. donnent aussi quelques exemples concrets d'heuristique admissible mais incohérente. Envisager la 8-puzzle problème:

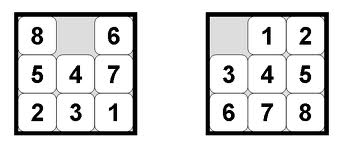
dans ce puzzle il y a 8 tuiles coulissantes numérotées 1-8, et un espace vide. Les carreaux commencent hors de l'ordre (comme dans l'image à gauche). Le but est d'amener le puzzle dans l'état montré ci-dessus sur la droite exclusivement en glissant des tuiles dans l'espace vide. L'heuristique classique pour ce problème (distance de Manhattan de chaque tuile à l'endroit où elle est censée être) est admissible et cohérente.

cependant, vous pourriez trouver un heuristique différent. Peut-être vous voulez juste regarder Manhattan distance (i.e. le nombre de carrés) du 1, le 2, et le 3 aux endroits dans lesquels ils sont censés être dans l'état de but. L'heuristique, bien que moins informative que la distance de Manhattan de toutes les tuiles, est encore admissible et cohérente.

Mais disons que vous choisissez un groupe supplémentaire de places, peut-être 5, 6, et 7. Et alors disons que la façon dont vous calculez l'heuristique à chaque noeud est en choisissant au hasard un de ces ensembles (1,2, et 3) ou (5, 6, et 7) et calculant leur distance de Manhattan à leur position de but. Cette heuristique est toujours recevable - il ne peut jamais sous-estimer ou égaler le nombre de mouvements nécessaires pour atteindre l'état du but. Cependant, il est n'est plus cohérent - il n'y a pas de relation claire entre les estimations heuristiques à chaque noeud.