intervalles de confiance et de prédiction avec les Modèles de statistiques
je fais cette régression linéaire avec StatsModels:
import numpy as np
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std
n = 100
x = np.linspace(0, 10, n)
e = np.random.normal(size=n)
y = 1 + 0.5*x + 2*e
X = sm.add_constant(x)
re = sm.OLS(y, X).fit()
print(re.summary())
prstd, iv_l, iv_u = wls_prediction_std(re)
mes questions sont, iv_l et <!-Les intervalles de confiance ou de prédiction sont-ils supérieurs et inférieurs? Comment j'en trouve d'autres? J'ai besoin des intervalles de confiance et de prédiction pour tous les points, pour faire un tracé.
4 réponses
iv_l et iv_u vous donner les limites de l'intervalle de prévision pour chaque point.
intervalle de Prédiction est l'intervalle de confiance pour une observation et inclut l'estimation de l'erreur.
je pense que, l'intervalle de confiance pour la moyenne de prédiction n'est pas encore disponible dans statsmodels.
(En fait, l'intervalle de confiance pour les valeurs ajustées se cache à l'intérieur du tableau synoptique de influence_outlier, mais je dois le vérifier.)
prédiction correcte les méthodes pour les modèles de statistiques sont sur la liste des choses à faire.
Ajout
les intervalles de confiance sont là pour les OLS mais l'accès est un peu maladroit.
Pour être inclus après l'exécution de votre script:
from statsmodels.stats.outliers_influence import summary_table
st, data, ss2 = summary_table(re, alpha=0.05)
fittedvalues = data[:, 2]
predict_mean_se = data[:, 3]
predict_mean_ci_low, predict_mean_ci_upp = data[:, 4:6].T
predict_ci_low, predict_ci_upp = data[:, 6:8].T
# Check we got the right things
print np.max(np.abs(re.fittedvalues - fittedvalues))
print np.max(np.abs(iv_l - predict_ci_low))
print np.max(np.abs(iv_u - predict_ci_upp))
plt.plot(x, y, 'o')
plt.plot(x, fittedvalues, '-', lw=2)
plt.plot(x, predict_ci_low, 'r--', lw=2)
plt.plot(x, predict_ci_upp, 'r--', lw=2)
plt.plot(x, predict_mean_ci_low, 'r--', lw=2)
plt.plot(x, predict_mean_ci_upp, 'r--', lw=2)
plt.show()
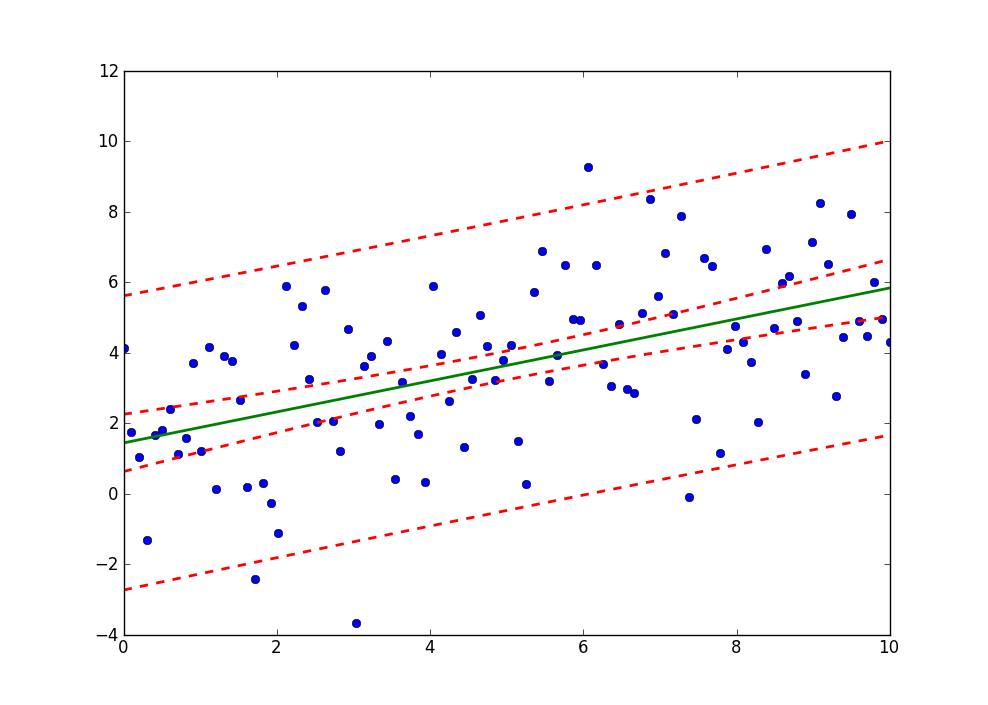
Cela devrait donner les mêmes résultats que SAS, http://jpktd.blogspot.ca/2012/01/nice-thing-about-seeing-zeros.html
Pour les données de test, vous pouvez essayer d'utiliser les éléments suivants.
predictions = result.get_prediction(out_of_sample_df)
predictions.summary_frame(alpha=0.05)
j'ai trouvé la méthode summy_frame() enfouie ici et vous pouvez trouver la méthode get_prediction ()ici. Vous pouvez modifier le niveau de signification de l'intervalle de confiance et l'intervalle de prédiction en modifiant le "alpha" de paramètre.
je poste ceci ici parce que c'était le premier poste qui se lève en cherchant une solution pour les intervalles de confiance et de prédiction – même si cela concerne plutôt les données d'essai.
Voici une fonction pour prendre un modèle, de nouvelles données, et un quantile arbitraire, en utilisant cette approche:
def ols_quantile(m, X, q):
# m: OLS model.
# X: X matrix.
# q: Quantile.
#
# Set alpha based on q.
a = q * 2
if q > 0.5:
a = 2 * (1 - q)
predictions = m.get_prediction(X)
frame = predictions.summary_frame(alpha=a)
if q > 0.5:
return frame.obs_ci_upper
return frame.obs_ci_lower
vous pouvez obtenir les intervalles de prédiction en utilisant la classe LRPI () à partir du bloc-notes Ipython dans mon repo (https://github.com/shahejokarian/regression-prediction-interval).
vous devez définir la valeur t pour obtenir l'intervalle de confiance désiré pour les valeurs de prédiction, sinon la valeur par défaut est 95% conf. intervalle.
la classe irpi utilise sklearn.linear_model de LinearRegression , numpy et les pandas bibliothèques.
il y a un exemple dans le portable trop.
summary_frame et summary_table travaillez bien quand vous avez besoin de résultats exacts pour un seul quantile, mais ne vectorisez pas bien. Ceci fournira une approximation normale de l'intervalle de prédiction (pas l'intervalle de confiance) et fonctionne pour un vecteur de quantiles:
def ols_quantile(m, X, q):
# m: Statsmodels OLS model.
# X: X matrix of data to predict.
# q: Quantile.
#
from scipy.stats import norm
mean_pred = m.predict(X)
se = np.sqrt(m.scale)
return mean_pred + norm.ppf(q) * se