Vérification de l'intersection de deux courbes de Bézier cubiques
pour un projet personnel, je dois savoir si deux courbes Bézier cubiques se croisent. Je n'ai pas besoin de savoir d'où: j'ai juste besoin de savoir si ils le font. Cependant, j'avais besoin de le faire rapidement.
j'ai fouillé l'endroit et j'ai trouvé plusieurs ressources. La plupart du temps, il y a cette question ici qui a eu une réponse prometteuse.
donc après que j'ai pensé ce qui est un matrice Sylvester , ce qui est un déterminant , ce qui est un résultant et pourquoi il est utile , j'ai pensé que je figurais comment la solution fonctionne. Cependant, la réalité est différente, et cela ne fonctionne pas si bien.
Déconner
j'ai utilisé ma calculatrice graphique pour dessiner deux lignes de Bézier (que nous appellerons B 0 et b 1 ) qui se croisent. Leur les coordonnées sont les suivantes (P 0 , P 1 , P 2 , P 3 ):
(1, 1) (2, 4) (3, 4) (4, 3)
(3, 5) (3, 6) (0, 1) (3, 1)
le résultat est le suivant, B 0 étant la courbe" horizontale "et B 1 l'autre:
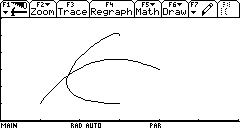
suivant les directives de la réponse à la question susmentionnée, j'ai soustrait B 0 à b 1 . Il m'a laissé avec deux équations (les axes X et Y) qui, selon ma calculatrice, sont:
x = 9t^3 - 9t^2 - 3t + 2
y = 9t^3 - 9t^2 - 6t + 4
La Matrice De Sylvester
et à partir de cela J'ai construit la matrice de Sylvester suivante:
9 -9 -3 2 0 0
0 9 -9 -3 2 0
0 0 9 -9 -3 2
9 -9 -6 4 0 0
0 9 -9 -6 4 0
0 0 9 -9 -6 4
après cela, j'ai fait une fonction C++ pour calculer les déterminants des matrices en utilisant Laplace expansion :
template<int size>
float determinant(float* matrix)
{
float total = 0;
float sign = 1;
float temporaryMatrix[(size - 1) * (size - 1)];
for (int i = 0; i < size; i++)
{
if (matrix[i] != 0)
{
for (int j = 1; j < size; j++)
{
float* targetOffset = temporaryMatrix + (j - 1) * (size - 1);
float* sourceOffset = matrix + j * size;
int firstCopySize = i * sizeof *matrix;
int secondCopySize = (size - i - 1) * sizeof *matrix;
memcpy(targetOffset, sourceOffset, firstCopySize);
memcpy(targetOffset + i, sourceOffset + i + 1, secondCopySize);
}
float subdeterminant = determinant<size - 1>(temporaryMatrix);
total += matrix[i] * subdeterminant * sign;
}
sign *= -1;
}
return total;
}
template<>
float determinant<1>(float* matrix)
{
return matrix[0];
}
il semble fonctionner assez bien sur des matrices relativement petites (2x2, 3x3 et 4x4), donc je m'attends à ce qu'il fonctionne sur des matrices 6x6 aussi. Je n'ai pas fait de tests approfondis, cependant, et il y a une possibilité qu'il soit cassé.
Le Problème
si j'ai bien compris la réponse de l'autre question, le déterminant devrait être 0 puisque les courbes se croisent. Cependant, nourrir mon programme de la matrice Sylvester que j'ai fait ci-dessus, c'est -2916.
est-ce une erreur de ma part ou de leur part? Quelle est la bonne façon de savoir si deux courbes Bézier cubiques se croisent?
8 réponses
Intersection des courbes de Bézier est fait par le (très cool) Asymptote langage graphique vectoriel: recherchez intersect() ici .
Bien qu'ils n'expliquent pas l'algorithme qu'ils utilisent réellement là-bas, sauf pour dire que c'est à partir de p. 137 de "La Metafont Livre", il semble que la clé est de deux propriétés importantes des courbes de Bézier (qui sont expliqués sur ce site mais je ne trouve pas la bonne page maintenant):
- une courbe de Bezier est toujours contenue dans la zone délimitée par ses 4 points de contrôle
- une courbe de Bezier peut toujours être subdivisée à un arbitraire t valeur en 2 sous-courbes de Bezier
avec ces deux propriétés et un algorithme pour intersecter les polygones, vous pouvez revenir à une précision arbitraire:
bezInt (B 1 , B 2 ):
- Ne bbox B 1 ) se croisent bbox B 2 )?
- : retourne la valeur false.
- Oui: Continuer.
- Est de la zone(bbox(B 1 )) + zone(bbox(B 2 )) < seuil?
- Oui: Return true.
- Pas de: Continuer.
- Split B 1 en B 1a et "B 1b à t = 0.5
- Split B 2 en B 2a et "B 2b à t = 0.5
- Return bezInt (B 1a , b 2a ) || bezInt (B 1a , B 2b ) / | bezInt (B 1b , b 2a ) / | bezInt (B 1b , b 2b ).
ce sera rapide si les courbes ne se croisent pas -- est-ce le cas habituel?
[EDIT] on dirait que l'algorithme pour séparer une courbe de Bézier en deux s'appelle l'algorithme de de Casteljau .
si vous faites ça pour le code de production, je suggérerais l'algorithme de découpage de Bezier. Il est bien expliqué dans section 7.7 de ce texte gratuit en ligne CAGD (pdf), fonctionne pour tout degré de courbe Bezier, et est rapide et robuste.
tout en utilisant rootfinders ou matrices standard pourrait être plus simple d'un point de vue mathématique, découpage Bezier est relativement facile à mettre en œuvre et déboguer, et aura en fait moins flottant point d'erreur. C'est parce que chaque fois qu'il crée de nouveaux nombres, il fait des moyennes pondérées (combinaisons convexes) de sorte qu'il n'y a aucune chance d'extrapoler basé sur des entrées bruyantes.
est-ce une erreur de ma part ou de leur part?
basez-vous votre interprétation du déterminant sur le 4ème Commentaire joint à cette réponse ? Si c'est le cas, je crois que c'est là que réside l'erreur. Reproduisant le commentaire ici:
Si le déterminant est nul il est une racine en X et Y à *exactement la même la valeur de t, donc il y a un l'intersection des deux courbe. (le t peut ne pas être dans l'intervalle 0..Un bien.)
Je ne vois aucun problème avec cette partie, mais l'auteur poursuit en disant:
Si le déterminant est <> zéro, vous pouvez assurez-vous que les courbes ne sont pas croiser n'importe où.
Je ne pense pas que ce soit correct. Il est parfaitement possible pour les deux courbes de se croiser dans un endroit où les valeurs de t diffèrent, et dans ce cas, il y aura une intersection même si la matrice a un déterminant non nul. Je crois que c'est ce qui se passe dans votre cas.
Je ne sais pas à quelle vitesse il sera, mais si vous avez deux courbes C1(t) et C2(k) ils se croisent si C1(t) == C2(k). Vous avez donc deux équations (par x et par y) de deux variables (t, k). Vous pouvez résoudre le système en utilisant des méthodes numériques avec assez de précision. Lorsque vous avez trouvé les paramètres t,k, vous devez vérifier s'il y a un paramètre sur [0, 1]. Si c'est le cas, ils se croisent sur [0, 1].
je suis pas un expert sur ce genre de chose, mais je suis un gentil blog qui parle beaucoup de courbes. Il a un lien vers deux beaux articles parlant de votre problème (le deuxième lien a une démonstration interactive et du code source). D'autres personnes peuvent avoir de mieux comprendre le problème, mais j'espère que cela aide!
C'est un problème difficile. Je diviserais chacune des 2 courbes de Bezier en 5-10 segments de ligne discrets, et je ferais juste des intersections ligne-ligne.
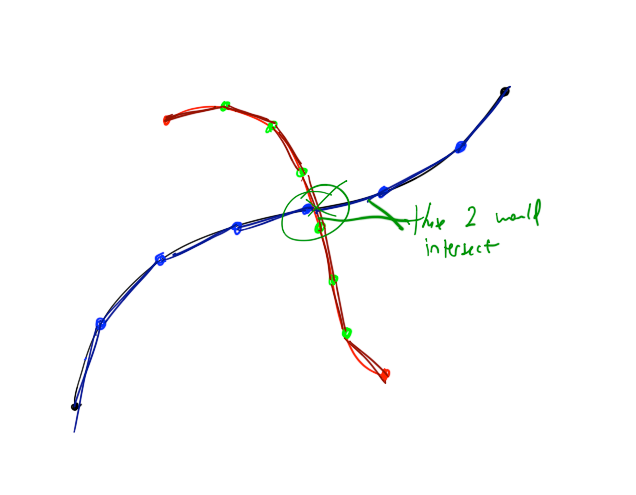
foreach SampledLineSegment line1 in Bezier1
foreach SampledLineSegment line2 in Bezier2
if( line1 intersects line2 )
then Bezier1 intersects Bezier2
je dirais que la réponse la plus facile et probablement la plus rapide est de les subdiviser en très petites lignes et de trouver les points où les courbes se croisent, si elles le font réellement.
public static void towardsCubic(double[] xy, double x0, double y0, double x1, double y1, double x2, double y2, double x3, double y3, double t) {
double x, y;
x = (1 - t) * (1 - t) * (1 - t) * x0 + 3 * (1 - t) * (1 - t) * t * x1 + 3 * (1 - t) * t * t * x2 + t * t * t * x3;
y = (1 - t) * (1 - t) * (1 - t) * y0 + 3 * (1 - t) * (1 - t) * t * y1 + 3 * (1 - t) * t * t * y2 + t * t * t * y3;
xy[0] = x;
xy[1] = y;
}
public static void towardsQuad(double[] xy, double x0, double y0, double x1, double y1, double x2, double y2, double t) {
double x, y;
x = (1 - t) * (1 - t) * x0 + 2 * (1 - t) * t * x1 + t * t * x2;
y = (1 - t) * (1 - t) * y0 + 2 * (1 - t) * t * y1 + t * t * y2;
xy[0] = x;
xy[1] = y;
}
évidemment, la réponse de la force brute est mauvaise voir la réponse de bo{4}, et il ya beaucoup de géométrie linéaire et de détection de collision qui va réellement aider beaucoup.
Choisissez le nombre de tranches que vous voulez pour les courbes. Quelque genre 100 devrait être génial.
Nous prenons tous les segments et les trier en fonction de la plus grande valeur de y ils ont. Nous ajoutons ensuite un second drapeau dans la liste pour la plus petite valeur de y pour ce segment.
nous gardons une liste des arêtes actives.
Nous parcourir l'axe liste triée de segment, lorsque nous rencontrons un segment principal, nous l'ajoutons à la liste active. Lorsque nous frappons la valeur Petit-y marqué, nous supprimons ce segment de l'active liste.
nous pouvons alors simplement itérer à travers l'ensemble des segments avec ce qui revient à une ligne de balayage, en augmentant notre y monotoniquement que nous itérons simplement la liste. Nous itérons les valeurs de notre liste triée, qui suppriment généralement un segment et en ajoutent un nouveau (ou pour séparer et fusionner des noeuds, ajouter deux segments ou supprimer deux segments). En gardant ainsi une liste active des segments pertinents.
nous effectuons le contrôle fast fail intersect pendant que nous ajouter un nouveau segment actif à la liste des parties actives, contre seulement ce segment et et l'active actuellement segments.
Donc, à tout moment, nous savons exactement quels segments de ligne sont pertinentes, comme nous parcourir l'échantillon de segments de courbes. Nous savons que ces segments se chevauchent dans les y-coords. Nous pouvons rapidement échouer tout nouveau segment qui ne se chevauche pas en ce qui concerne ses x-coords. Dans le cas rare qu'ils se chevauchent dans les X-coords, nous vérifions alors si ces segments croiser.
cela réduira probablement le nombre de vérifications d'intersection de lignes à essentiellement le nombre d'intersections.
foreach(segment in sortedSegmentList) {
if (segment.isLeading()) {
checkAgainstActives(segment);
actives.add(segment);
}
else actives.remove(segment)
}
checkAgainstActive () vérifierait simplement si ce segment et n'importe quel segment de la liste active chevauchent leurs x-coords, s'ils le font, puis lancerait la vérification de ligne intersect sur eux, et prendrait les mesures appropriées.
notez aussi, cela fonctionnera pour n'importe quel nombre de courbes, n'importe quel type de courbes, toute commande de courbes, de tout mélange. Et si nous itératons à travers la liste entière des segments il trouvera chaque intersection. Il trouvera chaque point un Bezier coupe un cercle ou chaque intersection qu'une douzaine de courbes Bezier quadratiques ont avec l'autre (ou eux-mêmes), et tout dans la même fraction de seconde.
La souvent cité Chapitre 7 du document , note, pour la subdivision de l'algorithme:
" une fois une paire de les courbes ont été suffisamment subdivisées pour que chacune puisse être approchée par un segment de ligne à l'intérieur d'une tolérance
on peut littéralement sauter l'intermédiaire. Nous pouvons le faire assez rapidement pour comparer simplement les segments de ligne avec une marge d'erreur tolérable de la courbe. En fin de compte, c'est ce que la réponse typique.
Deuxièmement, notez que l'essentiel de l'augmentation de vitesse pour la détection de collision ici, à savoir le commandé liste des segments triés en fonction de leur y le plus élevé à ajouter à la liste active, et y le plus bas à supprimer de la liste active, peut également être fait pour les polygones de coque de la courbe de Bezier directement. Notre segment de ligne est simplement un polygone de l'ordre 2, mais nous pourrions faire n'importe quel nombre de points tout aussi trivialement, et en cochant la boîte de limite de tous les points de contrôle dans n'importe quel ordre de courbe que nous traitons. Donc plutôt qu'une liste de segments actifs, nous aurions une liste de points de polygones de coque actifs. Nous pourrions simplement utiliser l'algorithme de de Casteljau pour diviser les courbes, échantillonnant ainsi que ceux-ci sous forme de courbes subdivisées plutôt que de segments de ligne. Donc, plutôt que 2 points, nous aurions 4 ou 7 ou autre chose, et exécuter la même routine étant tout à fait apte à l'échec rapide.
ajouter le groupe de points correspondant à max y, le supprimer à min y, et comparer seulement la liste active. Nous pouvons ainsi mettre en œuvre rapidement et mieux l'algorithme de subdivision de Bezier. En trouvant simplement la boîte de bounding le chevauchement, puis subdiviser les courbes qui se chevauchaient, et supprimer celles qui ne se chevauchaient pas. Comme, encore une fois, nous pouvons faire n'importe quel nombre de courbes, même ceux subdivisés des courbes dans l'itération précédente. Et comme notre approximation de segment résoudre rapidement pour chaque position d'intersection entre des centaines de courbes différentes (même de différents ordres) très rapidement. Il suffit de vérifier toutes les courbes pour voir si les boîtes limites se chevauchent, s'ils le font, nous subdiviser ceux, jusqu'à ce que nos courbes sont assez petites ou nous avons manqué de ils.
Oui, je sais, ce fil est accepté et fermé depuis longtemps, mais...
tout d'abord, je voudrais vous remercier, zneak , pour une inspiration. Votre effort permet de trouver le bon chemin.
deuxièmement, je n'étais pas très satisfait de la solution acceptée. Ce genre est utilisé dans mon IPE freeware préféré, et son bugzilla est beaucoup de plaintes pour une faible précision et la fiabilité sur une question d'intersection, mon parmi eux.
l'astuce manquante qui permet de résoudre le problème d'une manière proposée par zneak : il suffit de raccourcir une courbe par un facteur k" 1519190920 >0, alors le déterminant de la matrice Sylvester sera égal à zéro. Il est évident que si une courbe raccourcie se croise, alors original le fera aussi. Maintenant, la tâche est changée dans la recherche d'une valeur appropriée pour k facteur. Cela a conduit au problème de la résolution d'un polynôme univarié de 9 degrés. Une racine réelle et positive de ce polynôme est responsable de potentiels points d'intersection. (Cela ne devrait pas être une surprise, deux courbes de Bézier cubiques peuvent se croiser jusqu'à 9 fois.) La sélection finale est effectuée pour trouver seulement les facteurs k , qui fournissent 0<= t <=1 pour les deux courbes.
maintenant le code Maxima, où le point de départ est un ensemble de 8 points fourni par zneak :
p0x:1; p0y:1;
p1x:2; p1y:4;
p2x:3; p2y:4;
p3x:4; p3y:3;
q0x:3; q0y:5;
q1x:3; q1y:6;
q2x:0; q2y:1;
q3x:3; q3y:1;
c0x:p0x;
c0y:p0y;
c1x:3*(p1x-p0x);
c1y:3*(p1y-p0y);
c2x:3*(p2x+p0x)-6*p1x;
c2y:3*(p2y+p0y)-6*p1y;
c3x:3*(p1x-p2x)+p3x-p0x;
c3y:3*(p1y-p2y)+p3y-p0y;
d0x:q0x;
d0y:q0y;
d1x:3*(q1x-q0x);
d1y:3*(q1y-q0y);
d2x:3*(q2x+q0x)-6*q1x;
d2y:3*(q2y+q0y)-6*q1y;
d3x:3*(q1x-q2x)+q3x-q0x;
d3y:3*(q1y-q2y)+q3y-q0y;
x:c0x-d0x + (c1x-d1x*k)*t+ (c2x-d2x*k^2)*t^2+ (c3x-d3x*k^3)*t^3;
y:c0y-d0y + (c1y-d1y*k)*t+ (c2y-d2y*k^2)*t^2+ (c3y-d3y*k^3)*t^3;
z:resultant(x,y,t);
à ce point, Maxima a répondu:
(%o35)−2*(1004*k^9−5049*k^8+5940*k^7−1689*k^6+10584*k^5−8235*k^4−2307*k^3+1026*k^2+108*k+76)
que Maxima résolve cette équation:
rr: float( realroots(z,1e-20))
la réponse est:
(%o36) [k=−0.40256438624399,k=0.43261490325108,k=0.84718739982868,k=2.643321910825066,k=2.71772491293651]
maintenant le code pour sélectionner une valeur de droite de k :
for item in rr do (
evk:ev(k,item),
if evk>0 then (
/*print("k=",evk),*/
xx:ev(x,item), rx:float( realroots(xx,1e-20)),/*print("x(t)=",xx," roots: ",rx),*/
yy:ev(y,item), ry:float( realroots(yy,1e-20)),/*print("y(t)=",yy," roots: ",ry),*/
for it1 in rx do ( t1:ev(t,it1),
for it2 in ry do ( t2:ev(t,it2),
dt:abs(t1-t2),
if dt<1e-10 then (
/*print("Common root=",t1," delta t=",dt),*/
if (t1>0) and (t1<=1) then ( t2:t1*evk,
if (t2>0) and (t2<=1) then (
x1:c0x + c1x*t1+ c2x*t1^2+ c3x*t1^3,
y1:c0y + c1y*t1+ c2y*t1^2+ c3y*t1^3,
print("Intersection point: x=",x1, " y=",y1)
)))))/*,disp ("-----")*/
));
réponse de Maxima:
"Intersection point: x="1.693201254437358" y="2.62375005067273
(%o37) done
il n'y a pas qu'un miel, cependant. La méthode présentée est inutilisable si:
- P0=Q0, ou plus généralement, si P0 se trouve sur la deuxième courbe (ou son prolongement). On peut essayer de permuter les courbes.
- un cas extrêmement rare, lorsque les deux courbes appartiennent à une seule famille K (par ex. leurs extensions infinies sont les mêmes).
- keep an eyes on (sqr(c3x)+sqr (c3y))=0 ou (sqr(d3x)+sqr (3y))=0 cas, ici un quadratique prétendent être un cube courbes Bézier.
on peut se demander pourquoi un raccourcissement n'est effectué qu'une seule fois. C'est suffisant à cause de la loi inverse, qui a été découverte en passant , mais c'est une autre histoire.