Algorithme économique pour trouver la mesure de l'angle entre les vecteurs
trouver l'angle entre deux vecteurs n'est pas difficile en utilisant la règle de cosinus . Cependant, parce que je programmais pour une plate-forme avec des ressources très limitées, je voudrais éviter des calculs tels que sqrt et arccos . Même les divisions simples devraient être limitées autant que possible.
Heureusement, je n'ai pas besoin de l'angle en soi, mais seulement besoin d'une certaine valeur qui est proportionnelle à ladite angle.
alors je suis recherche d'un algorithme de calcul peu coûteux pour calculer une quantité qui est liée à l'angle entre deux vecteurs. Jusqu'à présent, je n'ai pas trouvé quelque chose qui correspond au projet de loi, et je n'ai pas été en mesure de trouver quelque chose moi-même.
9 réponses
avez-vous essayé un algorithme CORDIC ? Il s'agit d'un cadre général pour résoudre les problèmes rectangulaires polar ∆ avec seulement ajouter / soustraire / bitshift + table, essentiellement faire la rotation par les angles de la forme tan -1 (2 -n ). Vous pouvez compromis de précision avec des temps d'exécution en modifiant le nombre d'itérations.
dans votre cas, prenez un vecteur comme référence fixe, et copiez l'autre à un vecteur temporaire. vecteur, que vous faites pivoter en utilisant les angles cordiques vers le premier vecteur (à peu près bisection) jusqu'à ce que vous atteigniez une précision angulaire désirée.
( edit: utiliser le signe du produit scalaire de déterminer à chaque étape s'il faut faire pivoter vers l'avant ou vers l'arrière. Bien que si les multiples sont assez bon marché pour permettre l'utilisation de produit de point, alors ne vous embêtez pas avec CORDIC, peut-être utiliser une table de Sin / cos paires pour les matrices de rotation des angles π / 2 n pour résoudre le problème avec les non-bloquante.)
( edit: j'aime Eric Bainville de la suggestion dans les commentaires: faites pivoter les deux vecteurs vers zéro et de garder trace de la différence de l'angle.)
si vous n'avez pas besoin de l'angle euclidien réel, mais quelque chose que vous pouvez utiliser comme une base pour les comparaisons d'angle, puis changer à la géométrie taxicab peut être un choix, parce que vous pouvez laisser tomber la trigonométrie et il est la lenteur tout en maintenant la précision (ou au moins avec vraiment peu de perte de précision, voir ci-dessous).
navigateur moderne moteurs de l'accélération facteur est entre 1,44 - 15.2 et la précision est presque le même que dans atan2. Calcul de l'angle de diamant est en moyenne 5.01 fois plus rapide qu'atan2 et en utilisant le code inline dans Firefox 18 la speedup atteint le facteur 15.2. Comparaison de la vitesse: http://jsperf.com/diamond-angle-vs-atan2/2 .
le code est très simple:
function DiamondAngle(y, x)
{
if (y >= 0)
return (x >= 0 ? y/(x+y) : 1-x/(-x+y));
else
return (x < 0 ? 2-y/(-x-y) : 3+x/(x-y));
}
le code ci-dessus vous donne l'angle entre 0 et 4, tandis qu'atan2 vous donne l'angle entre-PI et PI comme le montre le tableau suivant:
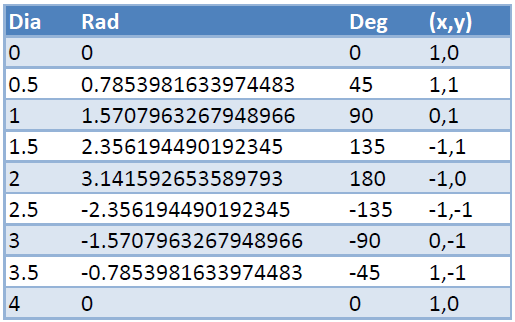
noter que l'angle de diamant est toujours positif et dans la gamme de 0-4, tandis qu'atan2 donne aussi des radians négatifs. Donc l'angle du diamant est plus normalisé. Et une autre note est qu'atan2 donne un résultat un peu plus précis, parce que la longueur de l'intervalle est de 2*pi (soit 6.283185307179586), alors que dans les angles diamantés il est de 4. Dans la pratique, cela n'est pas très important, par exemple. rad 2.300000000000000001 et 2.3000000000000002 sont tous les deux dans les angles de diamant 1.4718731421442295, mais si nous diminuons la précision par en laissant tomber un zéro, rad 2.300000000000001 et 2.300000000000002 donne à la fois un angle de diamant différent. Cette "perte de précision" dans les angles diamantés est si petite qu'elle n'a d'influence significative que si les distances sont énormes. Vous pouvez jouer avec des conversions dans http://jsbin.com/bewodonase/1/edit?output (ancienne version: http://jsbin.com/idoyon/1 ):
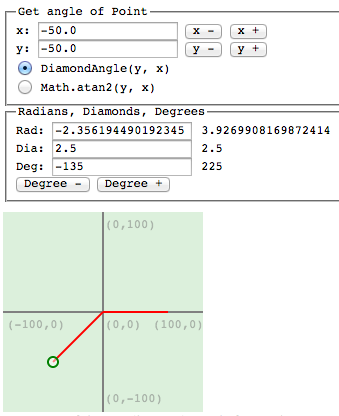
le code ci-dessus est suffisant pour des comparaisons d'angle rapides, mais dans de nombreux cas, il est nécessaire de convertir l'angle de diamant en radians et vice verca. Si par exemple vous. avoir une certaine tolérance comme angles radian, et puis vous avez une boucle de 100.000 fois où cette tolérance est comparée à d'autres angles, il n'est pas sage de faire des comparaisons en utilisant atan2. Au lieu de cela, avant de boucler, vous changez la tolérance de radian à la tolérance de taxicab (diamond angles) et faire des comparaisons en boucle en utilisant la tolérance de diamant et de cette façon, vous ne devez pas utiliser lent fonctions trigonométriques dans les parties critiques de la vitesse du code ( = dans les boucles).
le code qui fait cette conversion est ceci:
function RadiansToDiamondAngle(rad)
{
var P = {"x": Math.cos(rad), "y": Math.sin(rad) };
return DiamondAngle(P.y, P.x);
}
comme vous le constatez, il y a cos et sin . Comme vous le savez, ils sont lents, mais vous ne devez pas faire la conversion en boucle, mais avant la boucle et l'accélération est énorme.
et si pour une raison quelconque, vous devez convertir l'angle de diamant en radians, par exemple. après la boucle et de faire comparaisons d'angle pour retourner par exemple. l'angle minimal de comparaison ou quoi que ce soit comme radians, le code est le suivant:
function DiamondAngleToRadians(dia)
{
var P = DiamondAngleToPoint(dia);
return Math.atan2(P.y,P.x);
}
function DiamondAngleToPoint(dia)
{
return {"x": (dia < 2 ? 1-dia : dia-3),
"y": (dia < 3 ? ((dia > 1) ? 2-dia : dia) : dia-4)};
}
Ici, vous utilisez atan2 , qui est lent, mais l'idée est d'utiliser ce en dehors de toute boucle. Vous ne pouvez pas convertir l'angle de diamant en radians en se multipliant simplement par un facteur, mais au lieu de trouver un point dans la géométrie de taxicab dont l'angle de diamant entre ce point et l'axe X positif est l'angle de diamant en question et la conversion de ce point à radians utilisant atan2.
cela devrait suffire pour des comparaisons rapides d'angle.
bien sûr, il y a d'autres techniques d'accélération atan2 (par ex. CORDIC et tables de recherche), mais elles manquent toutes de précision et peuvent quand même être plus lentes que l'atan2.
contexte: j'ai testé plusieurs techniques: produits dot, produits intérieurs, loi du cosinus, cercles unitaires, tables de recherche, etc. mais rien n'était suffisant dans le cas où à la fois la vitesse et la précision sont important. Finalement j'ai trouvé une page dans http://www.freesteel.co.uk/wpblog/2009/06/encoding-2d-angles-without-trigonometry / qui avait les fonctions et les principes souhaités.
j'ai d'abord supposé que les distances taxicab pouvaient aussi être utilisées pour des comparaisons de distance précises et rapides, parce que la plus grande distance dans Euclide est plus grande aussi dans taxicab. J'ai réalisé que contrairement aux distances euclidiennes, l'angle entre le point de départ et le point final affecte le distance du taxi. Seules les longueurs de vecteurs verticaux et horizontaux peuvent être converties facilement et rapidement entre Euclide et taxicab, mais dans tous les autres cas vous devez tenir compte de l'angle et puis le processus est trop lent (?).
ainsi comme une conclusion je pense que dans les applications critiques de vitesse où est une boucle ou une récursion de plusieurs comparaisons d'angles et / ou de distances, les angles sont plus rapides à comparer dans l'espace de taxicab et les distances dans euclidienne (au carré, sans utilisation de l'espace sqrt).
de retour à l'époque de quelques K DE MÉMOIRE VIVE et machines avec des capacités mathématiques limitées, j'ai utilisé des tables de recherche et l'interpolation linéaire. L'idée de base est simple: créer un tableau avec autant de résolution que vous avez besoin (plus d'éléments réduisent l'erreur créée par interpolation). Puis interpoler entre les valeurs de recherche.
voici un exemple en cours de traitement ( lien mort original ).
Vous pouvez le faire avec votre d'autres fonctions trigonométriques. Sur le processeur 6502 cela a permis pour des graphiques de trame 3D complets d'être calculés avec un ordre de grandeur de l'augmentation de vitesse.
ici donc je n'ai toujours pas le privilège de commenter (bien que j'ai à math.se) donc ceci est en fait une réponse au post DE Timo sur diamond angles.
l'ensemble du concept d'angles diamantés basé sur la norme L1 est très intéressant et s'il s'agissait simplement d'une comparaison de quel vecteur a un W plus/moins grand.R. T. l'axe X positif serait suffisant. Cependant, L'OP a mentionné l'angle entre deux vecteurs génériques, et je présume que L'OP veut le comparer à certains la tolérance pour trouver l'état de lissage / coin ou sth comme cela, mais malheureusement, il semble qu'avec seulement les formules fournies sur jsperf.com ou freesteel.co.Royaume-Uni (liens ci-dessus) il semble qu'il ne soit pas possible de le faire en utilisant des angles diamantés.
Observe la sortie suivante de mon asymptote mise en œuvre des formules:
Vectors : 50,20 and -40,40
Angle diff found by acos : 113.199
Diff of angles found by atan2 : 113.199
Diamond minus diamond : 1.21429
Convert that to degrees : 105.255
Rotate same vectors by 30 deg.
Vectors : 33.3013,42.3205 and -54.641,14.641
Angle diff found by acos : 113.199
Diff of angles found by atan2 : 113.199
Diamond minus diamond : 1.22904
Convert that to degrees : 106.546
Rotate same vectors by 30 deg.
Vectors : 7.67949,53.3013 and -54.641,-14.641
Angle diff found by acos : 113.199
Diff of angles found by atan2 : 113.199
Diamond minus diamond : 1.33726
Convert that to degrees : 116.971
donc le point est que vous ne pouvez pas faire diamant (alpha) - diamant (bêta) et comparer à une certaine tolérance contrairement à ce que vous pouvez faire avec la sortie d'atan2. Si tout ce que vous voulez faire est diamond(alpha)>diamond(beta) alors je suppose que diamond est très bien.
la solution serait triviale si les vecteurs étaient définis/stockés en utilisant des coordonnées polaires au lieu de coordonnées cartésiennes (ou, 'ainsi que' en utilisant des coordonnées cartésiennes).
dot produit de deux vecteurs (x1, y1) et (x2, y2) est
x1 * x2 + y1 * y2
et est équivalent au produit des longueurs des deux vecteurs fois le cosinus de l'angle entre eux.
donc si vous normalisez les deux vecteurs en premier (divisez les coordonnées par la longueur)
Where length of V1 L1 = sqrt(x1^2 + y1^2),
and length of V2 L2 = sqrt(x2^2 + y2^2),
alors les vecteurs normalisés sont
(x1/L1, y1/L1), and (x2/L2, y2/L2),
et dot produit de vecteurs normalisés (qui est le même comme le cosinus de l'angle entre les vecteurs) serait
(x1*x2 + y1*y2)
-----------------
(L1*L2)
bien sûr, cela peut être aussi difficile sur le plan informatique que le calcul de la cosine
si vous avez besoin de calculer la racine carrée, alors envisager d'utiliser le invsqrt hack .
acos((x1*x2 + y1*y2) * invsqrt((x1*x1+y1*y1)*(x2*x2+y2*y2)));
La croix du produit est proportionnelle à l'angle entre deux vecteurs, et lorsque les vecteurs sont normalisés et l'angle est petit, le produit vectoriel est très proche de l'angle en radians en raison du faible angle de rapprochement.
spécifiquement:
I1Q2-I2Q1 est proportionnel à l'angle entre I1Q1 et I2Q2.
Le produit scalaire pourrait fonctionner dans votre cas. Ce n'est pas proportionnel à l'angle, mais "lié".