Champ D'Étoiles Rotatif De Canvas
je vais prendre l'approche suivante pour animer un champ d'étoiles à travers l'écran, mais je suis coincé pour la prochaine partie.
JS
var c = document.getElementById('stars'),
ctx = c.getContext("2d"),
t = 0; // time
c.width = 300;
c.height = 300;
var w = c.width,
h = c.height,
z = c.height,
v = Math.PI; // angle of vision
(function animate() {
Math.seedrandom('bg');
ctx.globalAlpha = 1;
for (var i = 0; i <= 100; i++) {
var x = Math.floor(Math.random() * w), // pos x
y = Math.floor(Math.random() * h), // pos y
r = Math.random()*2 + 1, // radius
a = Math.random()*0.5 + 0.5, // alpha
// linear
d = (r*a), // depth
p = t*d; // pixels per t
x = x - p; // movement
x = x - w * Math.floor(x / w); // go around when x < 0
(function draw(x,y) {
var gradient = ctx.createRadialGradient(x, y, 0, x + r, y + r, r * 2);
gradient.addColorStop(0, 'rgba(255, 255, 255, ' + a + ')');
gradient.addColorStop(1, 'rgba(0, 0, 0, 0)');
ctx.beginPath();
ctx.arc(x, y, r, 0, 2*Math.PI);
ctx.fillStyle = gradient;
ctx.fill();
return draw;
})(x, y);
}
ctx.restore();
t += 1;
requestAnimationFrame(function() {
ctx.clearRect(0, 0, c.width, c.height);
animate();
});
})();
HTML
<canvas id="stars"></canvas>
CSS
canvas {
background: black;
}
ce qu'il fait bien maintenant est animer chaque étoile avec un delta X qui considère l'opacité et la taille de l'étoile, de sorte que les plus petits semblent se déplacer plus lentement.
Utiliser p = t; pour avoir toutes les étoiles se déplaçant à la même vitesse.
QUESTION
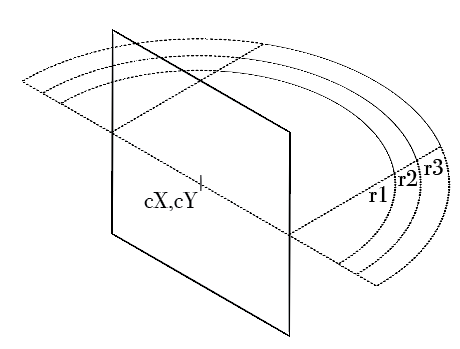
je suis à la recherche d'un modèle clairement défini où les vitesses donnent l'illusion des étoiles tournant autour de l'expectateur , défini en termes de le centre de la rotation cX, cY , et l'angle de vision v qui est quelle fraction de 2π peut être vu (si le centre du cercle n'est pas le centre de l'écran, le rayon doit être au moins la plus grande partie). Je me bats pour trouver un moyen qui applique ce cosinus à la vitesse des mouvements des étoiles, même pour un cercle centré avec une rotation de π.
ces diagrammes pourraient expliquer ce que je suis après:
Cercle centré:
Non centré:
angle de vision différent:
je suis vraiment perdu comment pour aller de l'avant. Je me suis déjà un peu étiré pour venir ici. Pouvez vous s'il vous plaît m'aider avec quelques premières étapes?
Merci
mise à jour
j'ai fait quelques progrès avec ce code:
// linear
d = (r*a)*z, // depth
v = (2*Math.PI)/w,
p = Math.floor( d * Math.cos( t * v ) ); // pixels per t
x = x + p; // movement
x = x - w * Math.floor(x / w); // go around when x < 0
Où p est la coordonnée x d'un particule en mouvement circulaire uniforme et v est la vitesse angulaire, mais cela génère un phénomène de balancier. Je ne suis pas sûr de savoir comment changer ces équations pour créer l'illusion que l'observateur tourne à la place.
Maj 2:
presque là. Un utilisateur du canal # # Math freenode a eu la gentillesse de proposer le calcul suivant:
// linear
d = (r*a), // depth
p = t*d; // pixels per t
x = x - p; // movement
x = x - w * Math.floor(x / w); // go around when x < 0
x = (x / w) - 0.5;
y = (y / h) - 0.5;
y /= Math.cos(x);
x = (x + 0.5) * w;
y = (y + 0.5) * h;
cela permet d'obtenir l'effet visuellement, mais ne suit pas un modèle clairement défini en termes de variables (il ne fait que "pirater" l'effet) de sorte que je ne peux pas voir une façon simple de faire différentes implémentations (changer le centre, angle de vision). Le vrai modèle pourrait être très similaire à celui-ci.
Maj 3
suite à la réponse D'Iftah, j'ai pu utiliser Sylvester pour appliquer une matrice de rotation aux étoiles, qui doivent être sauvegardées dans un tableau en premier. De plus, la coordonnée z de chaque étoile est maintenant déterminée et le rayon r et l'opacité a en sont dérivés. Le code est substantiellement différent et plus long donc je ne le poste pas, mais il pourrait être un pas dans la bonne direction. Je ne peux pas faire tourner ça continuellement. encore. L'utilisation d'opérations matricielles sur chaque trame semble coûteuse en termes de performance.
2 réponses
voici un pseudo qui fait ce dont vous parlez.
Make a bunch of stars not too far but not too close (via rejection sampling)
Set up a projection matrix (defines the camera frustum)
Each frame
Compute our camera rotation angle
Make a "view" matrix (repositions the stars to be relative to our view)
Compose the view and projection matrix into the view-projection matrix
For each star
Apply the view-projection matrix to give screen star coordinates
If the star is behind the camera skip it
Do some math to give the star a nice seeming 'size'
Scale the star coordinate to the canvas
Draw the star with its canvas coordinate and size
j'ai fait une mise en œuvre de ce qui précède. Il utilise la bibliothèque Javascript GL-matrix pour gérer une partie des mathématiques de matrix. C'est bien tout ça. (Violon pour cela est ici , ou voir ci-dessous.)
var c = document.getElementById('c');
var n = c.getContext('2d');
// View matrix, defines where you're looking
var viewMtx = mat4.create();
// Projection matrix, defines how the view maps onto the screen
var projMtx = mat4.create();
// Adapted from http://stackoverflow.com/questions/18404890/how-to-build-perspective-projection-matrix-no-api
function ComputeProjMtx(field_of_view, aspect_ratio, near_dist, far_dist, left_handed) {
// We'll assume input parameters are sane.
field_of_view = field_of_view * Math.PI / 180.0; // Convert degrees to radians
var frustum_depth = far_dist - near_dist;
var one_over_depth = 1 / frustum_depth;
var e11 = 1.0 / Math.tan(0.5 * field_of_view);
var e00 = (left_handed ? 1 : -1) * e11 / aspect_ratio;
var e22 = far_dist * one_over_depth;
var e32 = (-far_dist * near_dist) * one_over_depth;
return [
e00, 0, 0, 0,
0, e11, 0, 0,
0, 0, e22, e32,
0, 0, 1, 0
];
}
// Make a view matrix with a simple rotation about the Y axis (up-down axis)
function ComputeViewMtx(angle) {
angle = angle * Math.PI / 180.0; // Convert degrees to radians
return [
Math.cos(angle), 0, Math.sin(angle), 0,
0, 1, 0, 0,
-Math.sin(angle), 0, Math.cos(angle), 0,
0, 0, 0, 1
];
}
projMtx = ComputeProjMtx(70, c.width / c.height, 1, 200, true);
var angle = 0;
var viewProjMtx = mat4.create();
var minDist = 100;
var maxDist = 1000;
function Star() {
var d = 0;
do {
// Create random points in a cube.. but not too close.
this.x = Math.random() * maxDist - (maxDist / 2);
this.y = Math.random() * maxDist - (maxDist / 2);
this.z = Math.random() * maxDist - (maxDist / 2);
var d = this.x * this.x +
this.y * this.y +
this.z * this.z;
} while (
d > maxDist * maxDist / 4 || d < minDist * minDist
);
this.dist = Math.sqrt(d);
}
Star.prototype.AsVector = function() {
return [this.x, this.y, this.z, 1];
}
var stars = [];
for (var i = 0; i < 5000; i++) stars.push(new Star());
var lastLoop = Date.now();
function loop() {
var now = Date.now();
var dt = (now - lastLoop) / 1000.0;
lastLoop = now;
angle += 30.0 * dt;
viewMtx = ComputeViewMtx(angle);
//console.log('---');
//console.log(projMtx);
//console.log(viewMtx);
mat4.multiply(viewProjMtx, projMtx, viewMtx);
//console.log(viewProjMtx);
n.beginPath();
n.rect(0, 0, c.width, c.height);
n.closePath();
n.fillStyle = '#000';
n.fill();
n.fillStyle = '#fff';
var v = vec4.create();
for (var i = 0; i < stars.length; i++) {
var star = stars[i];
vec4.transformMat4(v, star.AsVector(), viewProjMtx);
v[0] /= v[3];
v[1] /= v[3];
v[2] /= v[3];
//v[3] /= v[3];
if (v[3] < 0) continue;
var x = (v[0] * 0.5 + 0.5) * c.width;
var y = (v[1] * 0.5 + 0.5) * c.height;
// Compute a visual size...
// This assumes all stars are the same size.
// It also doesn't scale with canvas size well -- we'd have to take more into account.
var s = 300 / star.dist;
n.beginPath();
n.arc(x, y, s, 0, Math.PI * 2);
//n.rect(x, y, s, s);
n.closePath();
n.fill();
}
window.requestAnimationFrame(loop);
}
loop();<script src="https://cdnjs.cloudflare.com/ajax/libs/gl-matrix/2.3.1/gl-matrix-min.js"></script>
<canvas id="c" width="500" height="500"></canvas>quelques liens:
mise à Jour
Voici une autre version qui a des commandes de clavier. Assez amusant. Vous pouvez voir la différence entre la rotation et la parallaxe de mitraillage. Qui fonctionne le mieux en pleine page. (Violon pour cela est ici ou voir ci-dessous.)
var c = document.getElementById('c');
var n = c.getContext('2d');
// View matrix, defines where you're looking
var viewMtx = mat4.create();
// Projection matrix, defines how the view maps onto the screen
var projMtx = mat4.create();
// Adapted from http://stackoverflow.com/questions/18404890/how-to-build-perspective-projection-matrix-no-api
function ComputeProjMtx(field_of_view, aspect_ratio, near_dist, far_dist, left_handed) {
// We'll assume input parameters are sane.
field_of_view = field_of_view * Math.PI / 180.0; // Convert degrees to radians
var frustum_depth = far_dist - near_dist;
var one_over_depth = 1 / frustum_depth;
var e11 = 1.0 / Math.tan(0.5 * field_of_view);
var e00 = (left_handed ? 1 : -1) * e11 / aspect_ratio;
var e22 = far_dist * one_over_depth;
var e32 = (-far_dist * near_dist) * one_over_depth;
return [
e00, 0, 0, 0,
0, e11, 0, 0,
0, 0, e22, e32,
0, 0, 1, 0
];
}
// Make a view matrix with a simple rotation about the Y axis (up-down axis)
function ComputeViewMtx(angle) {
angle = angle * Math.PI / 180.0; // Convert degrees to radians
return [
Math.cos(angle), 0, Math.sin(angle), 0,
0, 1, 0, 0,
-Math.sin(angle), 0, Math.cos(angle), 0,
0, 0, -250, 1
];
}
projMtx = ComputeProjMtx(70, c.width / c.height, 1, 200, true);
var angle = 0;
var viewProjMtx = mat4.create();
var minDist = 100;
var maxDist = 1000;
function Star() {
var d = 0;
do {
// Create random points in a cube.. but not too close.
this.x = Math.random() * maxDist - (maxDist / 2);
this.y = Math.random() * maxDist - (maxDist / 2);
this.z = Math.random() * maxDist - (maxDist / 2);
var d = this.x * this.x +
this.y * this.y +
this.z * this.z;
} while (
d > maxDist * maxDist / 4 || d < minDist * minDist
);
this.dist = 100;
}
Star.prototype.AsVector = function() {
return [this.x, this.y, this.z, 1];
}
var stars = [];
for (var i = 0; i < 5000; i++) stars.push(new Star());
var lastLoop = Date.now();
var dir = {
up: 0,
down: 1,
left: 2,
right: 3
};
var dirStates = [false, false, false, false];
var shiftKey = false;
var moveSpeed = 100.0;
var turnSpeed = 1.0;
function loop() {
var now = Date.now();
var dt = (now - lastLoop) / 1000.0;
lastLoop = now;
angle += 30.0 * dt;
//viewMtx = ComputeViewMtx(angle);
var tf = mat4.create();
if (dirStates[dir.up]) mat4.translate(tf, tf, [0, 0, moveSpeed * dt]);
if (dirStates[dir.down]) mat4.translate(tf, tf, [0, 0, -moveSpeed * dt]);
if (dirStates[dir.left])
if (shiftKey) mat4.rotate(tf, tf, -turnSpeed * dt, [0, 1, 0]);
else mat4.translate(tf, tf, [moveSpeed * dt, 0, 0]);
if (dirStates[dir.right])
if (shiftKey) mat4.rotate(tf, tf, turnSpeed * dt, [0, 1, 0]);
else mat4.translate(tf, tf, [-moveSpeed * dt, 0, 0]);
mat4.multiply(viewMtx, tf, viewMtx);
//console.log('---');
//console.log(projMtx);
//console.log(viewMtx);
mat4.multiply(viewProjMtx, projMtx, viewMtx);
//console.log(viewProjMtx);
n.beginPath();
n.rect(0, 0, c.width, c.height);
n.closePath();
n.fillStyle = '#000';
n.fill();
n.fillStyle = '#fff';
var v = vec4.create();
for (var i = 0; i < stars.length; i++) {
var star = stars[i];
vec4.transformMat4(v, star.AsVector(), viewProjMtx);
if (v[3] < 0) continue;
var d = Math.sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
v[0] /= v[3];
v[1] /= v[3];
v[2] /= v[3];
//v[3] /= v[3];
var x = (v[0] * 0.5 + 0.5) * c.width;
var y = (v[1] * 0.5 + 0.5) * c.height;
// Compute a visual size...
// This assumes all stars are the same size.
// It also doesn't scale with canvas size well -- we'd have to take more into account.
var s = 300 / d;
n.beginPath();
n.arc(x, y, s, 0, Math.PI * 2);
//n.rect(x, y, s, s);
n.closePath();
n.fill();
}
window.requestAnimationFrame(loop);
}
loop();
function keyToDir(evt) {
var d = -1;
if (evt.keyCode === 38) d = dir.up
else if (evt.keyCode === 37) d = dir.left;
else if (evt.keyCode === 39) d = dir.right;
else if (evt.keyCode === 40) d = dir.down;
return d;
}
window.onkeydown = function(evt) {
var d = keyToDir(evt);
if (d >= 0) dirStates[d] = true;
if (evt.keyCode === 16) shiftKey = true;
}
window.onkeyup = function(evt) {
var d = keyToDir(evt);
if (d >= 0) dirStates[d] = false;
if (evt.keyCode === 16) shiftKey = false;
}<script src="https://cdnjs.cloudflare.com/ajax/libs/gl-matrix/2.3.1/gl-matrix-min.js"></script>
<div>Click in this pane. Use up/down/left/right, hold shift + left/right to rotate.</div>
<canvas id="c" width="500" height="500"></canvas>Update 2
demande Alain Jacomet Forte:
Quelle est votre méthode recommandée pour créer la 3d polyvalente et si vous voulez recommander de travailler au niveau des matrices ou non, peut-être en particulier à ce scénario particulier.
concernant les matrices: si vous écrivez un moteur à partir de zéro sur n'importe quelle plate-forme, alors vous êtes inévitablement va finir par travailler avec des matrices car ils aident à généraliser les mathématiques 3D de base. Même si vous utilisez OpenGL / WebGL ou Direct3D, vous finirez toujours par créer une matrice de vue et de projection et des matrices supplémentaires pour des buts plus sophistiqués. (Manipulation de cartes normales, alignement d'objets mondiaux, dépeçage, etc...)
concernant une méthode de création de la 3d à usage général... Ne le fais pas. Il sera lent, et il ne sera pas performant sans beaucoup de travail. S'appuyer sur un matériel-bibliothèque accélérée pour faire le levage lourd. Créer des moteurs 3D limités pour des projets spécifiques est amusant et instructif (par exemple je veux une animation cool sur ma page Web), mais quand il s'agit de mettre les pixels sur l'écran pour quelque chose de sérieux, vous voulez que le matériel pour gérer cela autant que vous le pouvez à des fins de performance.
malheureusement, le web n'a pas encore de grand standard pour cela, mais il arrive en WebGL -- apprendre WebGL, utiliser WebGL. Il fonctionne bien et fonctionne bien quand il est soutenu. (Vous pouvez, cependant, vous en tirer avec un lot terrible juste en utilisant CSS 3D transforme et Javascript .)
si vous faites de la programmation de bureau, je recommande fortement OpenGL via SDL (Je ne suis pas encore vendu sur SFML) -- c'est multi-plateforme et bien supporté.
si vous programmez des téléphones mobiles, OpenGLES est à peu près votre seul choix (Autre qu'un dog-slow software renderer).
si vous voulez obtenir des trucs fait plutôt que d'écrire votre propre moteur à partir de zéro, le defacto pour le web est de trois.js (que je trouve efficace mais médiocre). Si vous voulez un moteur de jeu complet, Il ya quelques options gratuites ces jours-ci, les principaux commerciaux étant unité et irréel. Irrlicht a été autour d'un long temps -- n'a jamais eu une chance de l'utiliser, bien que, mais j'ai entendu dire que c'est bon.
mais si vous voulez faire toutes les choses 3D à partir de zéro... J'ai toujours trouvé comment le logiciel le locataire de Quake a fait une bonne étude de cas. Certains de ceux-ci peuvent être trouvés ici .
vous réinitialisez les étoiles 2D positionnez chaque image, puis déplacez les étoiles (en fonction du temps et de la vitesse de chaque étoile) - c'est une mauvaise façon d'atteindre votre objectif. Comme vous l'avez découvert, cela devient très complexe lorsque vous tentez d'étendre cette solution à d'autres scénarios.
une meilleure façon serait de définir l'emplacement des étoiles en 3d une seule fois (lors de l'initialisation) puis de déplacer une" caméra " à chaque image (en fonction du temps). Quand vous voulez rendre l'image 2d vous calculez alors étoiles emplacement sur l'écran. L'emplacement sur l'écran dépend de la stars 3d emplacement actuel et l'emplacement de la caméra. Cela vous permettra de déplacer la caméra (dans n'importe quelle direction), tourner la caméra (à n'importe quel angle) et rendre la position correcte des étoiles et de garder votre santé mentale.