calculez les points de retournement / pivotement de la trajectoire (trajectoire)
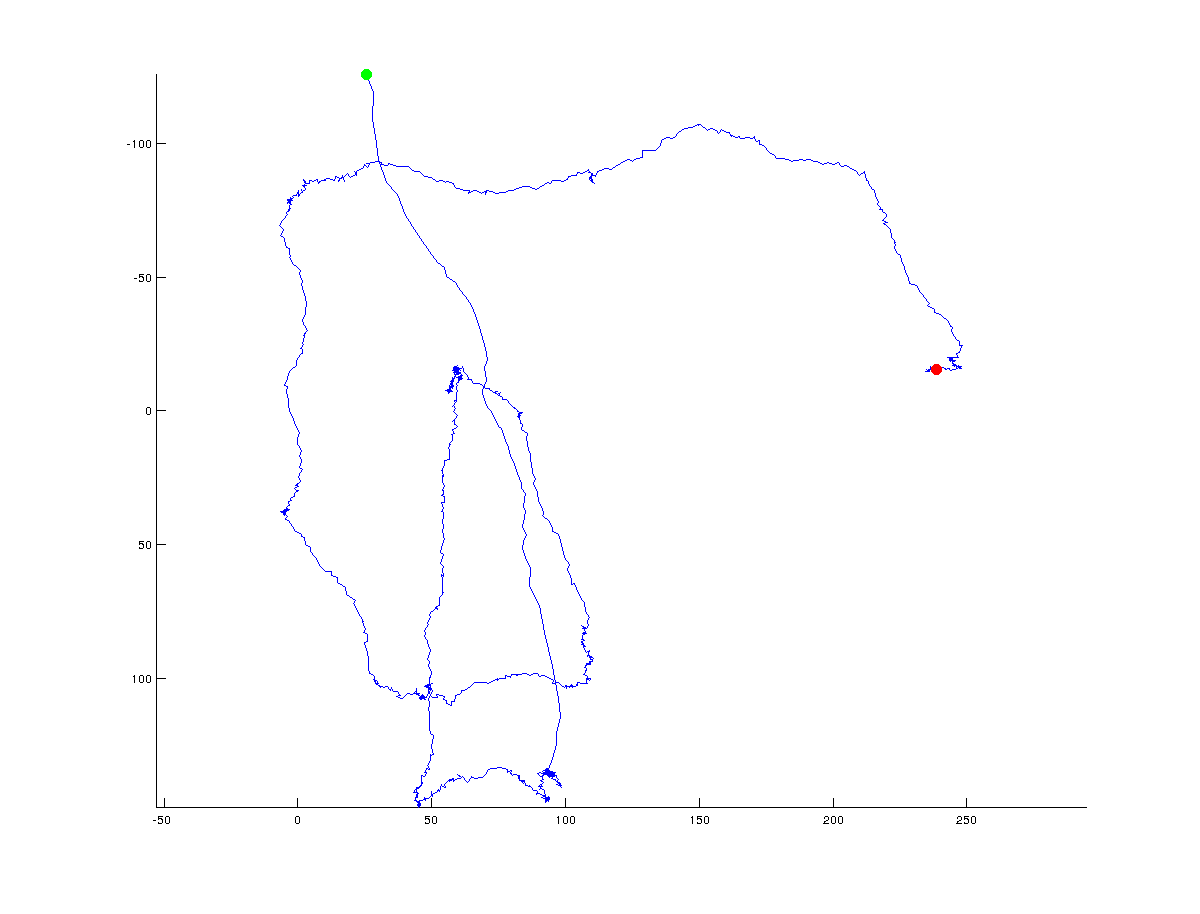
j'essaie de trouver un algorithme qui va déterminer les points de retournement dans une trajectoire de coordonnées x/Y. Les figures suivantes illustrent ce que je veux dire: vert indique le point de départ et rouge le point final de la trajectoire (toute la trajectoire se compose de ~ 1500 points):
dans la figure suivante, j'ai ajouté à la main les points de retournement possibles (globaux) qu'un algorithme pourrait retour:
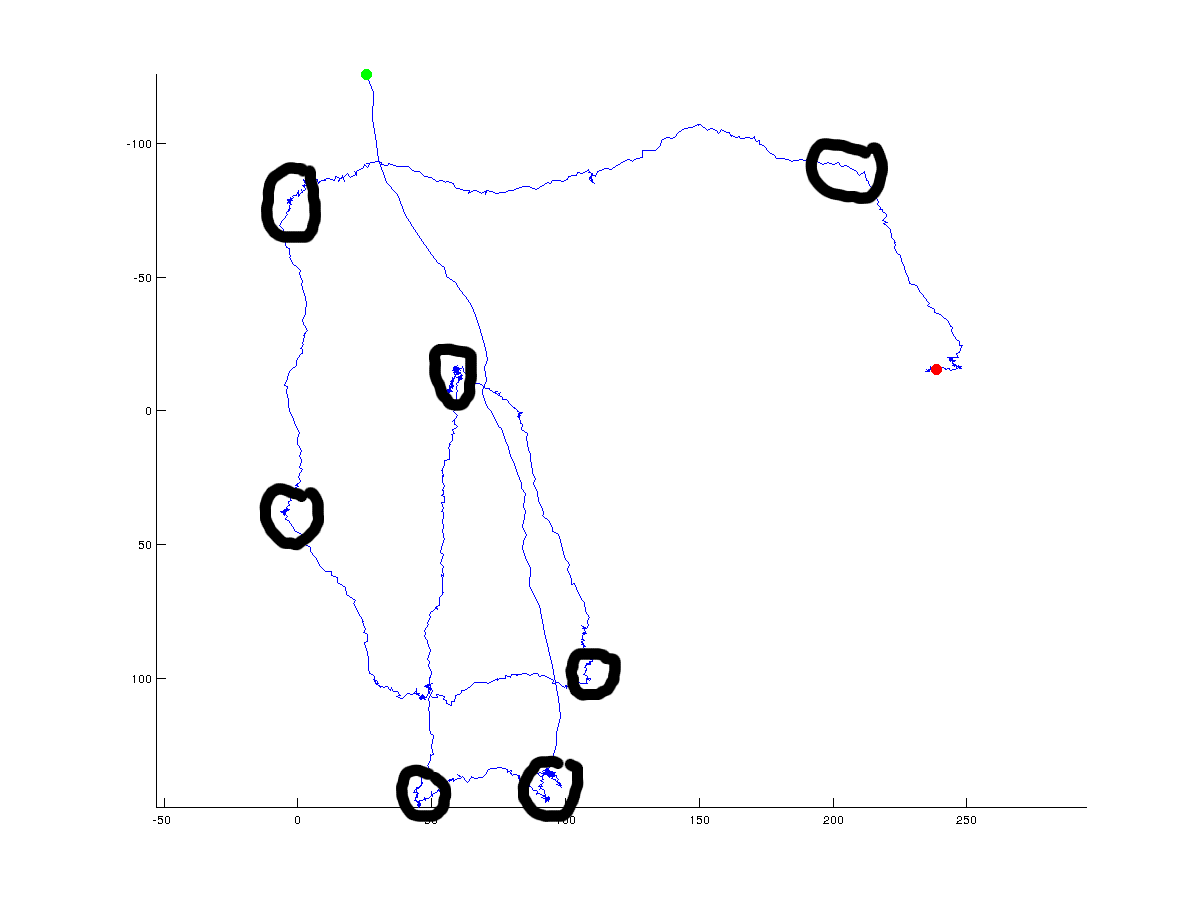
évidemment, le vrai point tournant est toujours discutable et dépendra de l'angle qu'on spécifie qui doit se trouver entre les points. En outre un tournant peut être défini à l'échelle globale (ce que j'ai essayé de faire avec les cercles noirs), mais pourrait également être définie sur une haute résolution à l'échelle locale. Je suis intéressé par les changements d'orientation globale (globale), mais j'aimerais voir une discussion sur les différentes approches que l'on utiliserait séparer les solutions globales des solutions locales.
Ce que j'ai essayé jusqu'à présent:
- calculer la distance entre les points suivants
- calculer l'angle entre les points suivants
- regardez à quelle distance / changements d'angle entre les points ultérieurs
malheureusement cela ne me donne pas de résultats robustes. J'ai probablement trop calculer la courbure le long de plusieurs points, mais c'est juste une idée. J'ai vraiment apprécier toutes les algorithmes / idées qui pourraient m'aider ici. Le code peut être dans n'importe quel langage de programmation matlab ou python sont privilégiées.
EDIT voici les données brutes (au cas où quelqu'un veut jouer avec elle):
- tapis de fichier
- fichier texte (coordonnée x d'abord, la coordonnée y dans la deuxième ligne)
5 réponses
vous pourriez utiliser le algorithme Ramer-Douglas-Peucker (RDP) pour simplifier la voie. Ensuite, vous pouvez calculer le changement de direction le long de chaque segment du chemin simplifié. Les points correspondant au plus grand changement de direction pourraient être appelés les tournants:
une implémentation Python de l'algorithme RDP peut être trouvée github.
import matplotlib.pyplot as plt
import numpy as np
import os
import rdp
def angle(dir):
"""
Returns the angles between vectors.
Parameters:
dir is a 2D-array of shape (N,M) representing N vectors in M-dimensional space.
The return value is a 1D-array of values of shape (N-1,), with each value
between 0 and pi.
0 implies the vectors point in the same direction
pi/2 implies the vectors are orthogonal
pi implies the vectors point in opposite directions
"""
dir2 = dir[1:]
dir1 = dir[:-1]
return np.arccos((dir1*dir2).sum(axis=1)/(
np.sqrt((dir1**2).sum(axis=1)*(dir2**2).sum(axis=1))))
tolerance = 70
min_angle = np.pi*0.22
filename = os.path.expanduser('~/tmp/bla.data')
points = np.genfromtxt(filename).T
print(len(points))
x, y = points.T
# Use the Ramer-Douglas-Peucker algorithm to simplify the path
# http://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm
# Python implementation: https://github.com/sebleier/RDP/
simplified = np.array(rdp.rdp(points.tolist(), tolerance))
print(len(simplified))
sx, sy = simplified.T
# compute the direction vectors on the simplified curve
directions = np.diff(simplified, axis=0)
theta = angle(directions)
# Select the index of the points with the greatest theta
# Large theta is associated with greatest change in direction.
idx = np.where(theta>min_angle)[0]+1
fig = plt.figure()
ax =fig.add_subplot(111)
ax.plot(x, y, 'b-', label='original path')
ax.plot(sx, sy, 'g--', label='simplified path')
ax.plot(sx[idx], sy[idx], 'ro', markersize = 10, label='turning points')
ax.invert_yaxis()
plt.legend(loc='best')
plt.show()
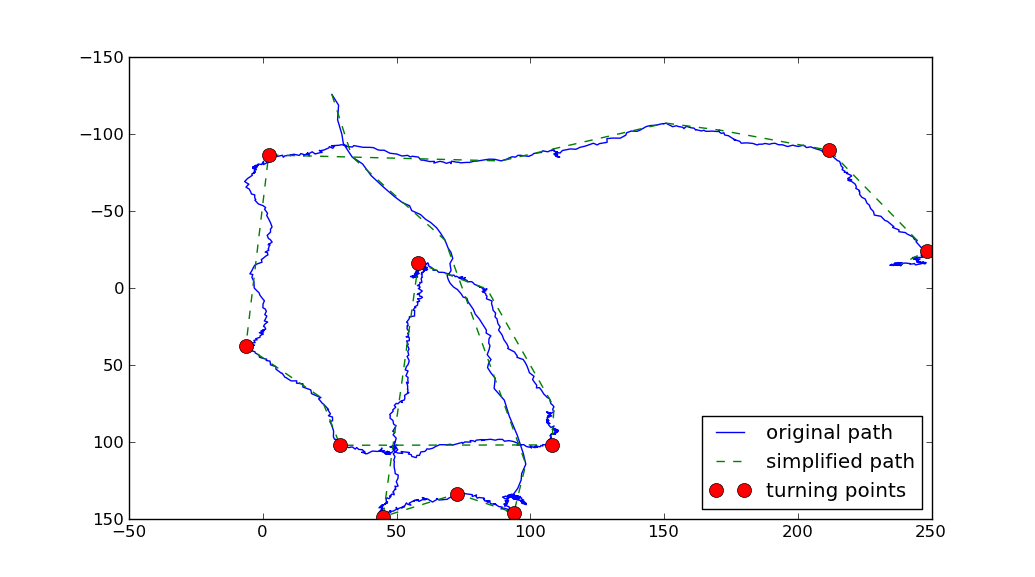
Deux paramètres ont été utilisés ci-dessus:
- l'algorithme RDP prend un paramètre, le
tolerance, qui représente la distance maximale le chemin simplifié peut s'écarter de la trajectoire initiale. La plus grande de l'tolerance, les plus rudimentaires le tracé simplifié. - L'autre paramètre est le
min_anglequi définit ce qui est considéré comme un tournant. (Je prends un point tournant pour être n'importe quel point sur le chemin original, dont l'angle entre les vecteurs entrant et sortant sur le chemin simplifié est plus grand quemin_angle).
je vais être de donner numpy/scipy code ci-dessous, que j'ai presque pas de Matlab expérience.
si votre courbe est assez lisse, vous pourriez identifier vos points de retournement comme étant les plus élevés courbure. En prenant le numéro d'indice de point comme paramètre de courbe, et un système central de différences, vous pouvez calculer la courbure avec le code suivant
import numpy as np
import matplotlib.pyplot as plt
import scipy.ndimage
def first_derivative(x) :
return x[2:] - x[0:-2]
def second_derivative(x) :
return x[2:] - 2 * x[1:-1] + x[:-2]
def curvature(x, y) :
x_1 = first_derivative(x)
x_2 = second_derivative(x)
y_1 = first_derivative(y)
y_2 = second_derivative(y)
return np.abs(x_1 * y_2 - y_1 * x_2) / np.sqrt((x_1**2 + y_1**2)**3)
vous voudrez probablement lisser votre courbe en premier, puis calculer la courbure, identifiez ensuite les points de courbure les plus élevés. La fonction suivante est juste que:
def plot_turning_points(x, y, turning_points=10, smoothing_radius=3,
cluster_radius=10) :
if smoothing_radius :
weights = np.ones(2 * smoothing_radius + 1)
new_x = scipy.ndimage.convolve1d(x, weights, mode='constant', cval=0.0)
new_x = new_x[smoothing_radius:-smoothing_radius] / np.sum(weights)
new_y = scipy.ndimage.convolve1d(y, weights, mode='constant', cval=0.0)
new_y = new_y[smoothing_radius:-smoothing_radius] / np.sum(weights)
else :
new_x, new_y = x, y
k = curvature(new_x, new_y)
turn_point_idx = np.argsort(k)[::-1]
t_points = []
while len(t_points) < turning_points and len(turn_point_idx) > 0:
t_points += [turn_point_idx[0]]
idx = np.abs(turn_point_idx - turn_point_idx[0]) > cluster_radius
turn_point_idx = turn_point_idx[idx]
t_points = np.array(t_points)
t_points += smoothing_radius + 1
plt.plot(x,y, 'k-')
plt.plot(new_x, new_y, 'r-')
plt.plot(x[t_points], y[t_points], 'o')
plt.show()
Quelques explications est dans l'ordre:
turning_pointsest le nombre de points que vous souhaitez identifiersmoothing_radiusest le rayon d'une convolution de lissage à appliquer à vos données avant de calculer la courburecluster_radiusest la distance à partir d'un point de courbure élevée sélectionné comme un point tournant où aucun autre point doit être considéré comme un candidat.
Vous pourriez avoir à jouer avec les paramètres un peu, mais j'ai eu quelque chose comme ceci:
>>> x, y = np.genfromtxt('bla.data')
>>> plot_turning_points(x, y, turning_points=20, smoothing_radius=15,
... cluster_radius=75)
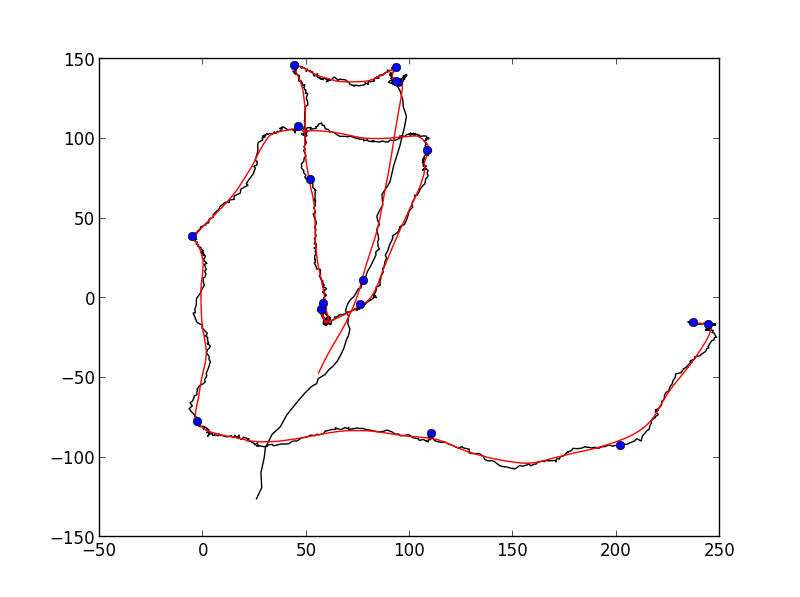
probablement pas assez bon pour une détection entièrement automatisée, mais il est assez proche de ce que vous vouliez.
Une question très intéressante. Voici ma solution, qui permet une résolution variable. Bien que, peaufiner il peut ne pas être simple, car il est la plupart du temps destiné à réduire
chaque k points, calculer la coque convexe et le stocker comme un ensemble. Passer par les points k au maximum et enlever les points qui ne sont pas dans la coque convexe, de telle sorte que les points ne perdent pas leur ordre d'origine.
le but ici est que la coque convexe agira comme un filtre, supprimer tous les "points sans importance" ne laissant que les points extrêmes. Bien sûr, si la valeur de k est trop élevée, vous finirez avec quelque chose de trop près de la coque convexe réelle, au lieu de ce que vous voulez réellement.
cela devrait commencer avec un petit k, au moins 4, puis l'augmenter jusqu'à ce que vous obtenez ce que vous recherchez. Vous devriez aussi probablement inclure seulement le point du milieu pour chaque 3 points où l'angle est inférieur à une certaine quantité, D. Cela permettrait de s'assurer que tous les virages sont au moins d degrés (non mis en œuvre dans le code ci-dessous). Toutefois, il faudrait probablement procéder de façon progressive pour éviter la perte d'information, tout comme l'augmentation de la valeur de K. Une autre amélioration possible serait de ré-exécuter avec des points qui ont été enlevés, et et seulement enlever les points qui n'étaient pas dans les deux coques convexes, bien que cela nécessite une valeur K-minimale plus élevée d'au moins 8.
le code suivant semble fonctionner assez bien, mais pourrait encore utiliser des améliorations pour l'efficacité et l'élimination du bruit. Il est également assez inélégant dans la détermination du moment où il devrait s'arrêter, donc le code ne fonctionne vraiment (tel qu'il est) que d'environ k=4 à k=14.
def convex_filter(points,k):
new_points = []
for pts in (points[i:i + k] for i in xrange(0, len(points), k)):
hull = set(convex_hull(pts))
for point in pts:
if point in hull:
new_points.append(point)
return new_points
# How the points are obtained is a minor point, but they need to be in the right order.
x_coords = [float(x) for x in x.split()]
y_coords = [float(y) for y in y.split()]
points = zip(x_coords,y_coords)
k = 10
prev_length = 0
new_points = points
# Filter using the convex hull until no more points are removed
while len(new_points) != prev_length:
prev_length = len(new_points)
new_points = convex_filter(new_points,k)
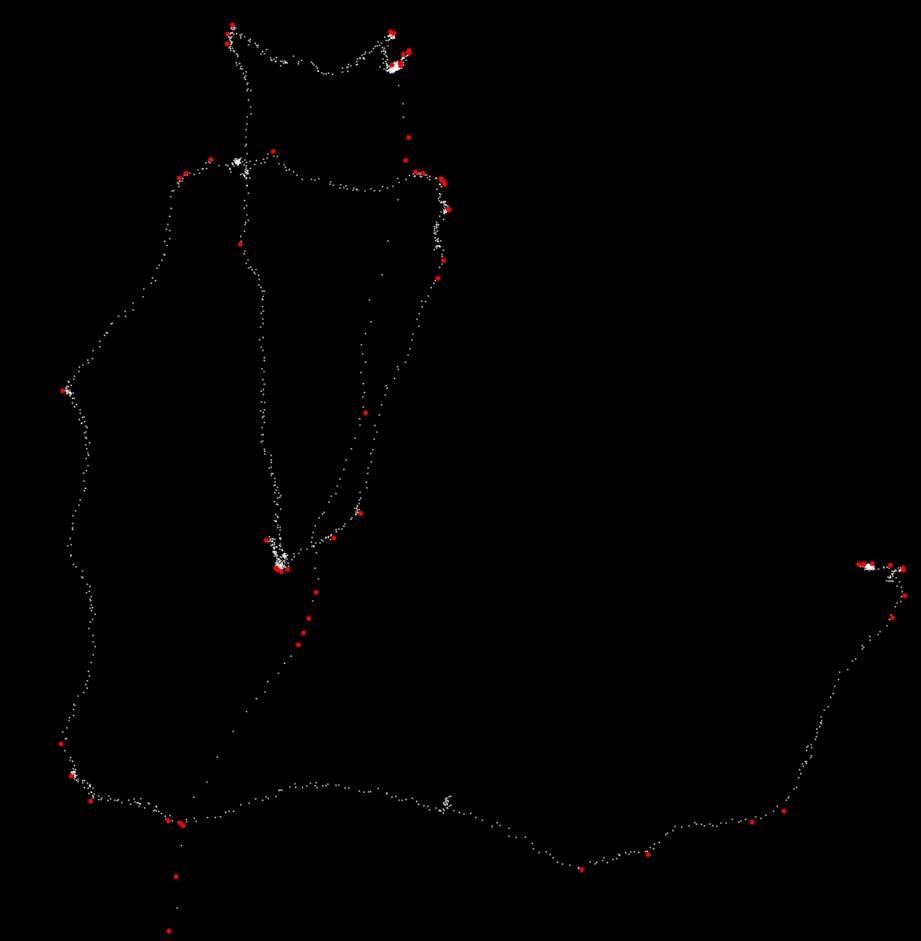
Voici une capture d'écran du code ci-dessus avec k=14. Les 61 points rouges sont ceux qui restent après le filtre.
l'approche que vous avez adoptée semble prometteuse, mais vos données sont largement suréchantillonnées. Vous pouvez filtrer les coordonnées x et y d'abord, par exemple avec un large Gaussien, puis sous-échantillonner.
Dans MATLAB, vous pouvez utiliser x = conv(x, normpdf(-10 : 10, 0, 5)) et x = x(1 : 5 : end). Vous devrez modifier ces nombres en fonction de la persistance intrinsèque des objets que vous suivez et de la distance moyenne entre les points.
ensuite, vous serez en mesure de détecter les changements de direction de manière très fiable, en utilisant la même approche que vous avez essayé avant, basé sur le produit scalaire, j'imagine.
une autre idée est d'examiner l'environnement à gauche et à droite à chaque point. Cela peut être fait en créant une régression linéaire de N points avant et après chaque point. Si l'angle d'intersection entre les points est en dessous d'un certain seuil, alors vous avez un coin.
cela peut être fait efficacement en gardant une file d'attente des points actuellement dans la régression linéaire et en remplaçant les anciens points par de nouveaux points, semblable à une moyenne courante.
Vous avez finalement à fusionner les coins adjacents à un seul coin. Par exemple: choisir le point avec la propriété coin le plus fort.