Calculer la température de couleur en K
J'ai écrit une lib pour travailler avec des couleurs et bloqué en essayant de calculer Tc(k). D'après ce que j'ai lu travailler dans le CIE 1931 XYZ l'espace colorimétrique est le chemin à parcourir et il peut être obtenu en utilisant xyY.
Jusqu'à présent, j'ai tout correct au point de trouver le bon x et y de:
X Y
x = ____________ y = ____________
( X + Y + Z) ( X + Y + Z)
Les Nombres jusqu'au graphique, mais ne peuvent pas trouver quoi que ce soit qui détaille comment vous allez de x et y à Tc(K)
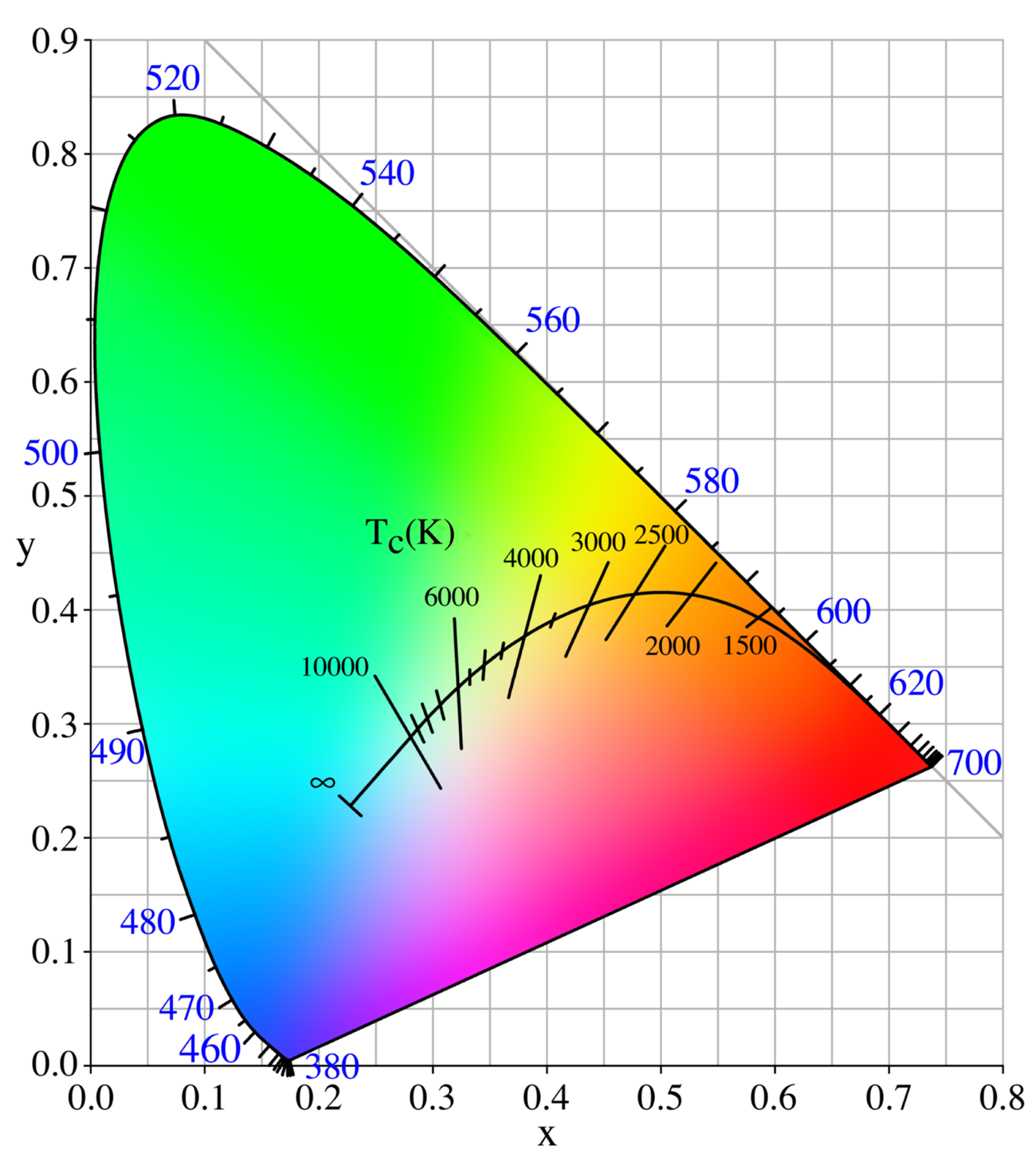
Par exemple: pour # FF0000 j'obtiens ce qui suit.
x: 0.64007449945677
y: 0.32997051063169
J'ai lu un certain nombre d'articles sur le sujet et littéralement tous les articles de wikipédia. Toutes les questions que j'ai rencontrées sur donc simplement un lien vers un article wiki sur les couleurs, pas vu celui qui a la formule réelle pour calculer Tc(k)
5 réponses
Si je vous comprends bien, veuillez voir ceci pdf où un certain nombre de méthodes (brièvement :( ) décrites. De ce PDF:
[CCT1] les calculs sont effectués à L'aide de L'espace colorimétrique uniforme CIE 1960 coordonnées u et v. Les coordonnées u et v sont dérivées de x et y en utilisant formule: u = 4x/(12y-2x+3) et v = 6y/(12y-2x+3) La température de couleur corrélée est définie comme la température d'un corps noir qui se trouve le plus proche des coordonnées u,v de la source d'essai. Deux méthodes distinctes fournissent résultats: l'une est une méthode itérative basée sur la définition, et l'autre est le méthode de Robertson couramment utilisée impliquant une interpolation basée sur un tableau de 30 paramètres U, v et pente inverse pré-calculés. Itération Si nous et vS sont les valeurs pour une source de test, et uT et vT sont les valeurs du corps noir à la température T, la température de couleur corrélée est la valeur de T où:
sqrt( (uS - uT)^2 + (vS - vT)^2 )
Est minimisé. Réglage de la température T pour obtenir le minimum de cette fonction a été fait en utilisant des feuilles de calcul (Quattro Pro 8 et Excel 97). Les deux feuilles de calcul ont donné des valeurs identiques.
Je ne sais pas si cela vous aide réellement.
Sur la base de L'article Wikipedia, j'ai entré la formule approximative pour le calcul de Color Temperature dans Excel comme
=(-449*((R1-0,332)/(S1-0,1858))^3)+(3525*((R1-0,332)/(S1-0,1858))^2)-(6823,3*((R1-0,332)/(S1-0,1858)))+(5520,33)
R1 is color space x coordinate from 0 to 1
S1 is color space y coordinate from 0 to 1
Fonctionne très bien!
J'ai fait quelques recherches dans certaines applications open source et j'ai trouvé quelque chose dans UFRaw. Je n'ai pas bien compris ce qui se passe exactement.
Aussi trouvé un papier, ce qui semble couvrir le sujet assez bien.
Converti en php et c'est ce que j'ai jusqu'à présent:
$temp = array(9500, 7000, 5500, 3750, 3000, 2700, 2250, 1800, 1500);
$hex = array('9DBEFF', 'E4EEFF', 'FFE4BE', 'FFA04C', 'FF7A26', 'FF6A19', 'FF500B', 'FF3403', 'FF2300');
echo '<h3>K -> RGB</h3>';
foreach ($temp as $k) {
$rgb = ColourConverter::temperature2rgb($k);
echo sprintf('<div style="background-color:rgb(%s); text-align: center; width: 100px; height: 25px; clear: both;">%s</div>', implode(', ', $rgb), $k);
}
echo '<h3>RGB -> K</h3>';
foreach ($hex as $v) {
$rgb = array_values(ColourConverter::hex2rgb($v));
$k = round(ColourConverter::rgb2temperature($rgb[0], $rgb[1], $rgb[2]));
echo sprintf('<div style="background-color:rgb(%s); text-align: center; width: 100px; height: 25px; clear: both;">%s</div>', implode(', ', $rgb), $k);
}

MA Sortie:
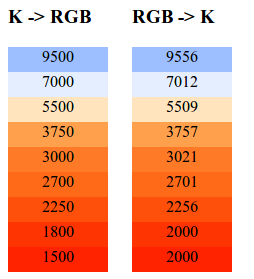
Assez proche mais pas encore à 100%. (Trouvé un bug dans mon code, et il est maintenant presque parfait)
- Les couleurs sont légèrement décalées aller de k - > rgb
- cela ne fonctionne pas en faisant k -> rgb -> K. Vous ne revenez pas à la même valeur.
Code
void Temperature_to_RGB(double T, double RGB[3])
{
int c;
double xD, yD, X, Y, Z, max;
// Fit for CIE Daylight illuminant
if (T <= 4000) {
xD = 0.27475e9 / (T * T * T) - 0.98598e6 / (T * T) + 1.17444e3 / T + 0.145986;
} else if (T <= 7000) {
xD = -4.6070e9 / (T * T * T) + 2.9678e6 / (T * T) + 0.09911e3 / T + 0.244063;
} else {
xD = -2.0064e9 / (T * T * T) + 1.9018e6 / (T * T) + 0.24748e3 / T + 0.237040;
}
yD = -3 * xD * xD + 2.87 * xD - 0.275;
// Fit for Blackbody using CIE standard observer function at 2 degrees
//xD = -1.8596e9/(T*T*T) + 1.37686e6/(T*T) + 0.360496e3/T + 0.232632;
//yD = -2.6046*xD*xD + 2.6106*xD - 0.239156;
// Fit for Blackbody using CIE standard observer function at 10 degrees
//xD = -1.98883e9/(T*T*T) + 1.45155e6/(T*T) + 0.364774e3/T + 0.231136;
//yD = -2.35563*xD*xD + 2.39688*xD - 0.196035;
X = xD / yD;
Y = 1;
Z = (1 - xD - yD) / yD;
max = 0;
for (c = 0; c < 3; c++) {
RGB[c] = X * XYZ_to_RGB[0][c] + Y * XYZ_to_RGB[1][c] + Z * XYZ_to_RGB[2][c];
if (RGB[c] > max) max = RGB[c];
}
for (c = 0; c < 3; c++) RGB[c] = RGB[c] / max;
}
void RGB_to_Temperature(double RGB[3], double *T, double *Green)
{
double Tmax, Tmin, testRGB[3];
Tmin = 2000;
Tmax = 23000;
for (*T = (Tmax + Tmin) / 2; Tmax - Tmin > 0.1; *T = (Tmax + Tmin) / 2) {
Temperature_to_RGB(*T, testRGB);
if (testRGB[2] / testRGB[0] > RGB[2] / RGB[0])
Tmax = *T;
else
Tmin = *T;
}
*Green = (testRGB[1] / testRGB[0]) / (RGB[1] / RGB[0]);
if (*Green < 0.2) *Green = 0.2;
if (*Green > 2.5) *Green = 2.5;
}
Wikipedia indique que la température de couleur est calculée en considérant les chromaticities u-v, PAS x-y, donc vous devez effectuer une traduction. Cela dit, je recommande d'utiliser une approximation (également expliquée dans Wikipedia) comme suggéré par @sixlettervariables.
La vraie question est-ce que vous essayez de trouver la température de couleur?. Je vois une référence (#FF0000) aux couleurs RVB, qui n'ont aucun sens sans indiquer d'espace colorimétrique. Supposons que vous êtes en sRGB (donc je peux vous pointez à Wikipedia Encore une fois), vous devez d'abord obtenir les coordonnées RVB linéaires avant de passer à XYZ.
Je me rends compte que c'est une vieille question, mais j'avais aussi du mal à trouver une réponse. Je suis finalement tombé sur cette calculatrice astucieuse qui affiche également la formule comme suit:
N = (x-0,3320)/(0,1858-y)
CCT = 437 * n^3 + 3601*n^2 + 6861*n + 5517
J'espère que cela aidera quelqu'un d'autre qui cherche encore.