Étendue première recherche analyse de la complexité
complexité temporelle pour passer en revue chaque bord adjacent d'un sommet est dit O(N), où N est le nombre de bords adjacents. Ainsi, pour V nombre de vertices, la complexité du temps devient O(V*N)= O(E), où E est le nombre total de bords dans le graphique. Depuis supprimer et Ajouter un vertex de / à la file d'attente est O(1), pourquoi il est ajouté à la complexité temporelle globale de BFS comme O(V+E).
4 réponses
en considérant le graphique suivant nous voyons comment la complexité temporelle est O (|V|+| E/) mais pas O (V*E).
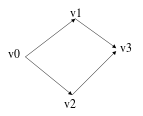
Liste De Contiguïté
V E
v0:{v1,v2}
v1:{v3}
v2:{v3}
v3:{}
Comment BFS Fonctionne étape par Étape
Etape 1:
listes de contiguïté:
V E
v0: {v1,v2} mark, enqueue v0
v1: {v3}
v2: {v3}
v3: {}
Etape 2:
listes de contiguïté:
V E
v0: {v1,v2} dequeue v0;mark, enqueue v1,v2
v1: {v3}
v2: {v3}
v3: {}
Step 3:
listes de contiguïté:
V E
v0: {v1,v2}
v1: {v3} dequeue v1; mark,enqueue v3
v2: {v3}
v3: {}
Step 4:
contiguïté listes:
V E
v0: {v1,v2}
v1: {v3}
v2: {v3} dequeue v2, check its adjacency list (v3 already marked)
v3: {}
Step 5:
listes de contiguïté:
V E
v0: {v1,v2}
v1: {v3}
v2: {v3}
v3: {} dequeue v3; check its adjacency list
Step 6:
listes de contiguïté:
V E
v0: {v1,v2} |E0|=2
v1: {v3} |E1|=1
v2: {v3} |E2|=1
v3: {} |E3|=0
nombre Total de pas:
|V| + |E0| + |E1| + |E2| +|E3| == |V|+|E|
4 + 2 + 1 + 1 + 0 == 4 + 4
8 == 8
supposons une représentation de liste de contiguïté, V est le nombre de Sommets, E le nombre de bords.
chaque vertex est interrogé et débité au plus une fois.
la recherche de tous les sommets adjacents prend O (/E/)de temps, puisque la somme des longueurs de les listes de contiguïté sont / E/.
D'où la complexité temporelle DE BFS donne un O (/V / +| E/) le temps de la complexité.
j'espère que cela sera utile à quiconque ayant de la difficulté à comprendre la complexité du temps de calcul pour une première recherche étendue A. K. a BFS.
Queue graphTraversal.add(firstVertex);
// This while loop will run V times, where V is total number of vertices in graph.
while(graphTraversal.isEmpty == false)
currentVertex = graphTraversal.getVertex();
// This while loop will run Eaj times, where Eaj is number of adjacent edges to current vertex.
while(currentVertex.hasAdjacentVertices)
graphTraversal.add(adjacentVertex);
graphTraversal.remove(currentVertex);
V * (O(1) + O(Eaj) + O(1))
V + V * Eaj + V
2V + E(total number of edges in graph)
V + E
j'ai essayé de simplifier le code et la complexité de calcul, mais si vous avez des questions laissez-moi savoir.
Spectacle O(1) opération L fois, les résultats de O(L) complexité.
Ainsi, supprimer et Ajouter un vertex de/à la file d'attente est O( 1), mais quand vous faites cela pour V vertices, vous obtenez O(V) complexité.
Par conséquent, O(V) + O(E) = O(V+E)
les autres réponses ici font un excellent travail en montrant comment fonctionne BFS et comment l'analyser. Je voulais revoir votre analyse mathématique originale pour montrer où, spécifiquement, votre raisonnement vous donne une estimation inférieure à la vraie valeur.
Votre analyse va comme ceci:
- soit N Le nombre moyen d'arêtes incidentes à chaque noeud (N = E / V).
- chaque noeud, par conséquent, passe O (N) temps à effectuer des opérations sur la file d'attente.
- Puisqu'il n'y sont des noeuds V, la durée totale d'exécution est O(V) · O(N) = O(V) · O(E / V) = O(E).
vous êtes très près d'avoir la bonne estimation ici. La question Est de savoir d'où vient le terme V manquant. La question ici est que, assez bizarrement, vous ne pouvez pas dire que O(V) · o(E / V) = O(e).
vous avez totalement raison que le travail moyen par noeud est O (E / V). Cela signifie que le travail total réalisé asympotically est limité d'en haut par un certain multiple de E / V. Si nous pensez à ce que BFS fait réellement, le travail effectué par noeud ressemble probablement plus à c1 + c2 E / V, puisqu'il y a un peu de travail de base fait par noeud (mise en place de boucles, vérification des conditions de base, etc.), ce qui est pris en compte par le c1 durée, plus une certaine quantité de travail proportionnelle au nombre d'arêtes visitées (E / V, fois le travail effectué par arête). Si nous multiplions ceci par V, nous obtenons cela
V · (c1 + c2 E / V)
= c1 V + c2 E
= Θ (V + E)
ce qui se passe ici, c'est que ces charmants Termes d'ordre inférieur que big-O nous laisse si commodément ignorer sont en fait importants ici, donc nous ne pouvons pas facilement les écarter. Donc c'est mathématiquement au moins ce qui se passe.
Que en fait, ce qui se passe ici est que peu importe combien de bords il y a dans le graphique, il y a une quantité de base de travail que vous devez faire pour chaque noeud indépendamment de ces bords. C'est la configuration pour faire des choses comme exécuter les instructions core if, configurer les variables locales, etc.