Boxplots in matplotlib: marqueurs et valeurs aberrantes
j'ai quelques questions à propos de boxplots dans matplotlib:
Question A. Que font les marqueurs que j'ai mis en évidence ci-dessous avec T1,T2 et T3 représenter? Je crois T1 est maximale et T3 sont des valeurs aberrantes, mais ce qui est T2<!--8?
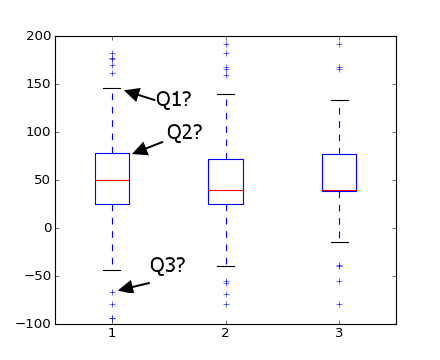
Question B Comment identifier matplotlib valeurs aberrantes<!--8? (c'est à dire comment sait-elle qu'ils ne sont pas le vrai max et min valeurs?)
6 réponses
Une image vaut mille mots. Notez que les valeurs aberrantes (+ marqueurs dans votre parcelle) sont simplement des points dehors de la large [(Q1-1.5 IQR), (Q3+1.5 IQR)] marge ci-dessous.
cependant, l'image n'est qu'un exemple pour un ensemble de données normalement distribué. Il est important de comprendre que matplotlib fait estimer d'abord une distribution normale et calculer les quartiles à partir des paramètres de distribution estimés comme suit: indiqué ci-dessus.
au Lieu de cela, la médiane et les quartiles sont calculés directement à partir des données. Ainsi, votre boxplot peut sembler différent selon la distribution de vos données et la taille de l'échantillon, par exemple, asymétrique et avec plus ou moins de valeurs aberrantes.
la case représente le premier et le troisième quartiles, avec la ligne rouge la médiane (2e quartile). documentation donne les whiskers par défaut à 1.5 IQR:
boxplot(x, notch=False, sym='+', vert=True, whis=1.5,
positions=None, widths=None, patch_artist=False,
bootstrap=None, usermedians=None, conf_intervals=None)
et
whis : [ par défaut 1.5 ]
définit la longueur des moustaches en fonction du quartile interne. Elles s'étendent jusqu'au point de données le plus extrême à l'intérieur de la plage de données whis*(75% -25%).
Si vous êtes confus au sujet de différentes représentations graphiques en boîte essayez de lire la description dans wikipedia.
en plus de la réponse de seth (puisque la documentation n'est pas très précise à ce sujet)): Q1 (les wiskers) sont placés à la valeur maximale en dessous de 75% + 1,5 IQR
(valeur minimale de 25% - 1,5 IQR)
voici le code qui calcule la position des moustaches:
# get high extreme
iq = q3 - q1
hi_val = q3 + whis * iq
wisk_hi = np.compress(d <= hi_val, d)
if len(wisk_hi) == 0 or np.max(wisk_hi) < q3:
wisk_hi = q3
else:
wisk_hi = max(wisk_hi)
# get low extreme
lo_val = q1 - whis * iq
wisk_lo = np.compress(d >= lo_val, d)
if len(wisk_lo) == 0 or np.min(wisk_lo) > q1:
wisk_lo = q1
else:
wisk_lo = min(wisk_lo)
juste au cas où cela pourrait profiter à quelqu'un d'autre, j'ai eu besoin de mettre une légende sur un de mes graphiques de tracé de boîte donc j'ai fait ce peu .png dans Inkscape et j'ai pensé le partager.
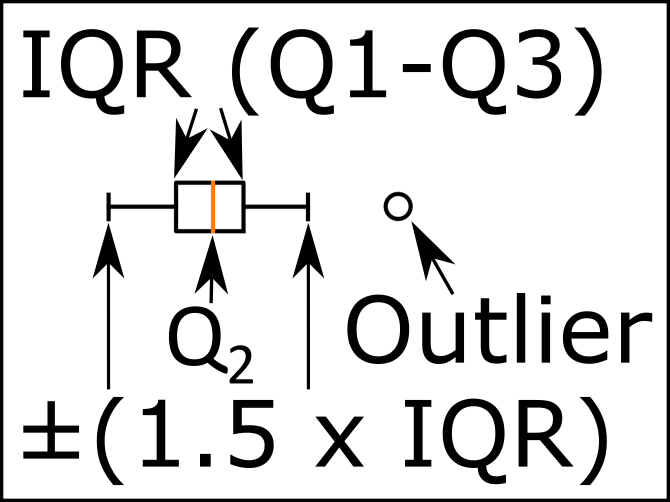
l'image ci-dessous montre les différentes parties d'un boxplot.
Quantile 1 / Q1: 25e Percentile
médiane (Quantile 2/Q2): 50e Percentile.
Quantile 3 / Q3: 75e Percentile.
je dois noter que la partie bleue sont les moustaches du boxplot.
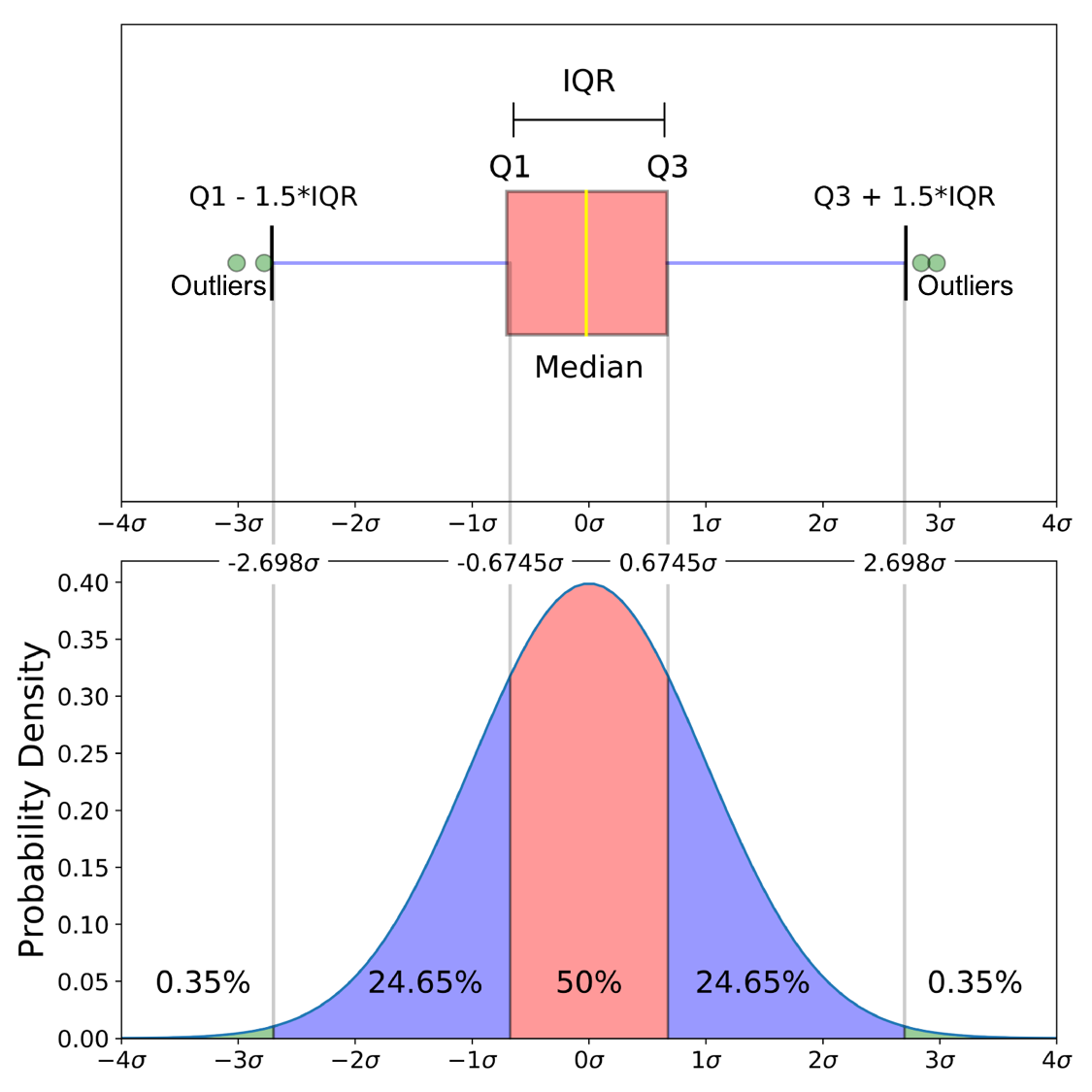
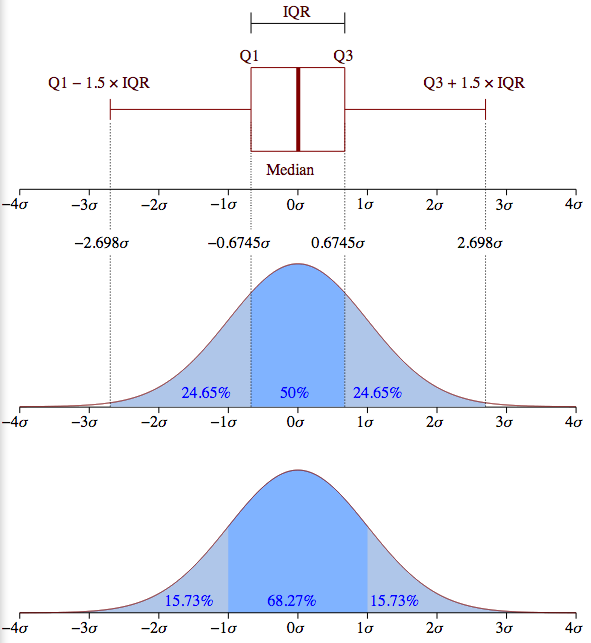
l'image ci-dessous compare le tracé de la boîte de une distribution normale contre la fonction de densité de probabilité. Cela devrait aider à expliquer le "Minimum", le "Maximum" et les valeurs aberrantes.
"Minimum": (Q1 - 1.5 IQR)
"Maximum": (Q3+1.5 IQR)
comme zelusp l'a dit, 99,3% des données sont contenues dans 2.698 σ (écarts-types) pour une distribution normale. Les cercles verts (valeurs aberrantes) dans l'image ci-dessous sont les autres .7% des données. Ici est un comment ces nombres sont arrivés à être.
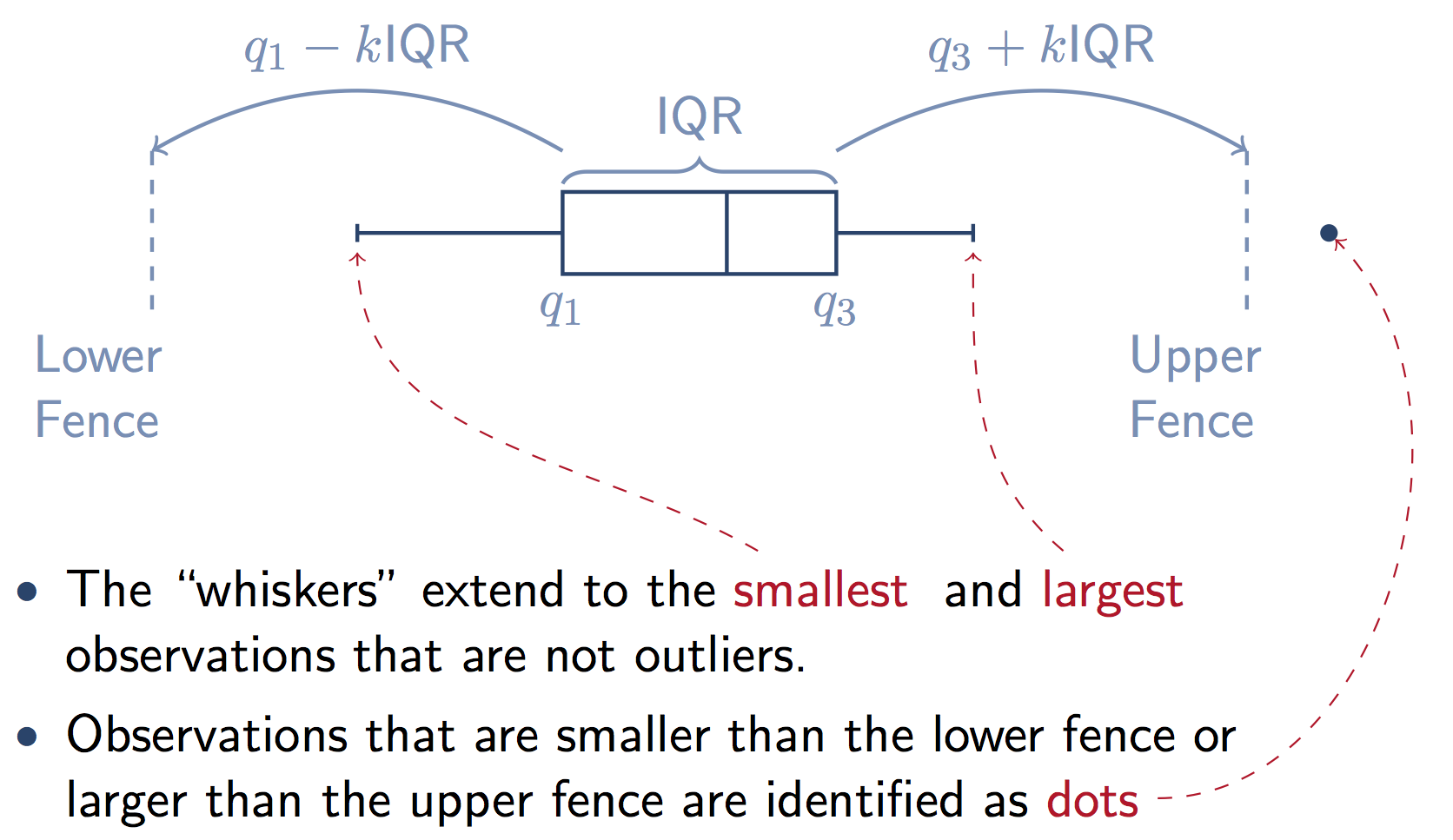
Voici un graphique qui illustre les composants de la boîte à partir d'un statistiques.stackexchange réponse. Notez que k=1.5 si vous ne fournissez pas le whis mot clé dans Pandas.
la fonction boxplot dans Pandas est un wrapper pour matplotlib.pyplot.boxplot. matplotlib docs expliquer en détail les composantes des cases:
Question A:
La zone s'étend de la les valeurs des quartiles inférieur à Supérieur des données, avec une ligne à la médiane.