Calcul de la longueur Base64?
Après avoir lu le base64 wiki ...
J'essaie de comprendre Comment fonctionne la formule:
Étant donné une chaîne de n, La longueur base64 sera 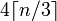
, Qui est : 4*Math.Ceiling(((double)s.Length/3)))
Je sais déjà que la longueur base64 doit être %4==0 pour permettre au décodeur de savoir quelle était la longueur du texte d'origine.
, Le nombre maximal de remplissage pour une séquence peut être = ou ==.
Wiki: le nombre de sorties octets par octet d'entrée est d'environ 4 / 3 (33% frais généraux)
Question:
Comment les informations ci-dessus s'installer avec la longueur de sortie 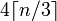 ?
?
11 réponses
Chaque caractère est utilisé pour représenter 6 bits (log2(64) = 6).
Par conséquent, 4 caractères sont utilisés pour représenter 4 * 6 = 24 bits = 3 bytes.
Si vous avez besoin d' 4*(n/3) caractères pour représenter n octets, et ce doit être arrondi à un multiple de 4.
Le nombre de inutilisés rembourrage de caractères résultant de l'arrondi à un multiple de 4 sera évidemment 0, 1, 2 ou 3.
4 * n / 3 donne la longueur non rembourrée.
Et arrondir au multiple le plus proche de 4 pour le remplissage, et comme 4 est une puissance de 2 peut utiliser des opérations logiques au niveau du BIT.
((4 * n / 3) + 3) & ~3
Pour référence, la formule de longueur de l'encodeur Base64 est la suivante:
Comme vous l'avez dit, un encodeur Base64 donné n octets de données produira une chaîne de 4n/3 caractères Base64. Autrement dit, tous les 3 octets de données donneront 4 caractères Base64. modifier: un commentaire souligne correctement que mon graphique précédent ne tenait pas compte du remplissage; la formule correcte est Ceiling(4n/3).
L'article Wikipedia montre exactement comment la chaîne ASCII Man codée dans la chaîne Base64 TWFu dans son exemple. La chaîne d'entrée est de 3 octets, ou 24 bits, de sorte que la formule prédit correctement que la sortie sera longue de 4 octets (ou 32 bits): TWFu. Le processus code tous les 6 bits de données dans l'un des 64 caractères Base64, de sorte que l'entrée 24 bits divisée par 6 résulte en 4 caractères Base64.
Vous demandez dans un commentaire quelle serait la taille de l'encodage 123456. En gardant à l'esprit que chaque chaque caractère de cette la chaîne est de 1 octet, ou 8 bits, en taille (en supposant un codage ASCII / UTF8), nous codons 6 octets, ou 48 bits, de données. Selon l'équation, Nous nous attendons à ce que la longueur de sortie soit (6 bytes / 3 bytes) * 4 characters = 8 characters.
Mettre 123456 dans un encodeur Base64 crée MTIzNDU2, qui a 8 caractères, comme prévu.
Je pense que les réponses données manquent le point de la question originale, qui est de savoir combien d'espace doit être alloué pour s'adapter à l'encodage base64 pour une chaîne binaire donnée de longueur n octets.
La réponse est (floor(n / 3) + 1) * 4 + 1
Cela inclut le remplissage et un caractère nul de fin. Vous n'avez peut-être pas besoin de l'appel floor si vous faites de l'arithmétique entière.
Y compris le remplissage, une chaîne base64 nécessite quatre octets pour chaque bloc de trois octets de la chaîne d'origine, y compris tout morceau. Un ou deux octets supplémentaires à la fin de la chaîne seront toujours convertis en quatre octets dans la chaîne base64 lorsque le remplissage est ajouté. Sauf si vous avez un usage très spécifique, il est préférable d'ajouter le remplissage, généralement égal caractère. J'ai ajouté un octet supplémentaire pour un caractère nul dans C, car les chaînes ASCII sans cela sont un peu dangereuses et vous devez porter la longueur de la chaîne séparément.
Entiers
Généralement, nous ne voulons pas utiliser de doubles parce que nous ne voulons pas utiliser les opérations à virgule flottante, les erreurs d'arrondi, etc. Ils sont tout simplement pas nécessaires.
Pour cela, il est une bonne idée de se rappeler comment effectuer la division de plafond: ceil(x / y) en doubles peut être écrit comme (x + y - 1) / y (tout en évitant les nombres négatifs, mais méfiez-vous des débordements).
Lisible
Si vous optez pour la lisibilité, vous pouvez bien sûr aussi le programmer comme ceci (exemple en Java, pour C vous peut utiliser des macros, bien sûr):
public static int ceilDiv(int x, int y) {
return (x + y - 1) / y;
}
public static int paddedBase64(int n) {
int blocks = ceilDiv(n, 3);
return blocks * 4;
}
public static int unpaddedBase64(int n) {
int bits = 8 * n;
return ceilDiv(bits, 6);
}
// test only
public static void main(String[] args) {
for (int n = 0; n < 21; n++) {
System.out.println("Base 64 padded: " + paddedBase64(n));
System.out.println("Base 64 unpadded: " + unpaddedBase64(n));
}
}
Inline
Collier de
Nous savons que nous avons besoin de 4 blocs de caractères à la fois pour chaque 3 octets (ou moins). Alors la formule devient (pour x = N et y = 3):
blocks = (bytes + 3 - 1) / 3
chars = blocks * 4
Ou combinés:
chars = ((bytes + 3 - 1) / 3) * 4
Votre compilateur optimisera le 3 - 1, Alors laissez-le comme ceci pour maintenir la lisibilité.
Non rembourré
Moins commun est la variante non rembourrée, pour cela nous nous souvenons que chacun nous avons besoin d'un caractère pour chaque 6 bits, arrondis:
bits = bytes * 8
chars = (bits + 6 - 1) / 6
Ou combinés:
chars = (bytes * 8 + 6 - 1) / 6
, Nous pouvons cependant encore diviser par deux (si on veut):
chars = (bytes * 4 + 3 - 1) / 3
Illisible
Si vous ne faites pas confiance à votre compilateur pour faire les optimisations finales pour vous (ou si vous voulez confondre vos collègues):
Collier de
((n + 2) / 3) << 2
Non rembourré
((n << 2) | 2) / 3
Nous voilà donc, deux méthodes logiques de calcul, et nous n'en avons pas besoin branches, bit-ops ou modulo ops-sauf si nous le voulons vraiment.
Notes:
- évidemment, vous devrez peut-être ajouter 1 aux calculs pour inclure un octet de terminaison nul.
- pour Mime, vous devrez peut-être prendre soin des caractères de terminaison de ligne possibles et autres (cherchez d'autres réponses pour cela).
Voici une fonction pour calculer la taille d'origine d'un fichier de base 64 codé sous forme de chaîne en Ko:
private Double calcBase64SizeInKBytes(String base64String) {
Double result = -1.0;
if(StringUtils.isNotEmpty(base64String)) {
Integer padding = 0;
if(base64String.endsWith("==")) {
padding = 2;
}
else {
if (base64String.endsWith("=")) padding = 1;
}
result = (Math.ceil(base64String.length() / 4) * 3 ) - padding;
}
return result / 1000;
}
Me semble que la bonne formule devrait être:
n64 = 4 * (n / 3) + (n % 3 != 0 ? 4 : 0)
Alors que tout le monde débat des formules algébriques, je préfère simplement utiliser BASE64 lui-même pour me dire:
$ echo "Including padding, a base64 string requires four bytes for every three-byte chunk of the original string, including any partial chunks. One or two bytes extra at the end of the string will still get converted to four bytes in the base64 string when padding is added. Unless you have a very specific use, it is best to add the padding, usually an equals character. I added an extra byte for a null character in C, because ASCII strings without this are a little dangerous and you'd need to carry the string length separately."| wc -c
525
$ echo "Including padding, a base64 string requires four bytes for every three-byte chunk of the original string, including any partial chunks. One or two bytes extra at the end of the string will still get converted to four bytes in the base64 string when padding is added. Unless you have a very specific use, it is best to add the padding, usually an equals character. I added an extra byte for a null character in C, because ASCII strings without this are a little dangerous and you'd need to carry the string length separately." | base64 | wc -c
710
Il semble donc que la formule de 3 octets étant représentée par 4 caractères base64 semble correcte.
Dans windows - je voulais estimer la taille du tampon de taille mime64, mais toutes les formules de calcul précises ne fonctionnaient pas pour moi-enfin je me suis retrouvé avec une formule approximative comme ceci:
Taille d'allocation de chaîne Mine64 (approximative) = (((4 * ((Taille du tampon binaire) + 1)) / 3) + 1)
Donc last + 1-Il est utilisé pour ascii-zero - le dernier caractère doit être alloué pour stocker la fin zéro - mais pourquoi "Taille du tampon binaire" est + 1 - je soupçonne qu'il y a un caractère de terminaison mime64? Ou peut-être que c'est un problème d'alignement.
Implémentation Simple en javascript
function sizeOfBase64String(base64String) {
if (!base64String) return 0;
const padding = (base64String.match(/(=*)$/) || [])[1].length;
return 4 * Math.ceil((base64String.length / 3)) - padding;
}
Je crois que celui-ci est une réponse exacte si n % 3 Pas zéro, non ?
(n + 3-n%3)
4 * ---------
3
Version Mathematica:
SizeB64[n_] := If[Mod[n, 3] == 0, 4 n/3, 4 (n + 3 - Mod[n, 3])/3]
Amusez-vous
GI