Collision balle à balle-détection et manipulation

Question

Collision balle à balle-détection et manipulation

Avec L'aide de la communauté Stack Overflow, j'ai écrit un simulateur de physique assez basique mais amusant.

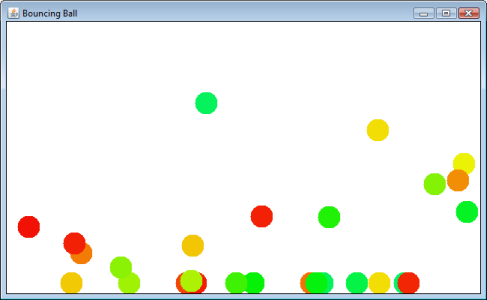
le texte d'alt

Vous cliquez et faites glisser la souris pour lancer une balle. Il rebondira et finira par s'arrêter sur le "sol".

Ma prochaine grande fonctionnalité que je veux ajouter Est balle à balle collision. Le mouvement de la balle est divisé en un vecteur de vitesse x et Y. J'ai la gravité (petite réduction du vecteur y à chaque étape), j'ai la friction (petite réduction des deux vecteurs chacun collision avec un mur). Les balles se déplacent honnêtement d'une manière étonnamment réaliste.

Je suppose que ma question a deux parties:

Quelle est la meilleure méthode pour détecter la collision balle à balle?
Est-ce que j'ai juste une boucle O(N^2) qui itère sur chaque balle et vérifie toutes les autres balles pour voir si son Rayon se chevauche?
quelles équations dois-je utiliser pour gérer les collisions balle à balle? La physique 101
Comment cela affecte-t-il les deux balles speed x / y les vecteurs? Quelle est la direction résultante dans laquelle les deux balles se dirigent? Comment puis-je appliquer cela à chaque balle?

le texte d'alt

Gérer la détection de collision des "murs" et les changements de vecteurs qui en résultent était facile, mais je vois plus de complications avec les collisions balle-balle. Avec les murs, je devais simplement prendre le négatif du vecteur X ou y approprié et l'éteindre irait dans la bonne direction. Avec les couilles, Je ne pense pas que ce soit comme ça.

Quelques clarifications rapides: pour simplicité je suis ok avec une collision parfaitement élastique pour l'instant, aussi toutes mes balles ont la même masse en ce moment, mais je pourrais changer cela à l'avenir.

Edit: ressources que j'ai trouvées utiles

Physique Des Billes 2d avec vecteurs: Collisions à 2 Dimensions sans trigonométrie.pdf
Exemple de détection de collision de balle 2D: ajout de la détection de Collision

Succès!

J'ai la balle collision détection et Réponse de travail Très bien!

Code pertinent:

Détection De Collision:

for (int i = 0; i < ballCount; i++)  
{  
    for (int j = i + 1; j < ballCount; j++)  
    {  
        if (balls[i].colliding(balls[j]))  
        {
            balls[i].resolveCollision(balls[j]);
        }
    }
}

Cela vérifiera les collisions entre chaque balle mais ignorera les vérifications redondantes (si vous devez vérifier si la balle 1 entre en collision avec la balle 2, vous n'avez pas besoin de vérifier si la balle 2 entre en collision avec la balle 1. En outre, il ignore la vérification des collisions avec lui-même).

Ensuite, dans ma classe de balle, j'ai mes méthodes colliding () et resolveCollision ():

public boolean colliding(Ball ball)
{
    float xd = position.getX() - ball.position.getX();
    float yd = position.getY() - ball.position.getY();

    float sumRadius = getRadius() + ball.getRadius();
    float sqrRadius = sumRadius * sumRadius;

    float distSqr = (xd * xd) + (yd * yd);

    if (distSqr <= sqrRadius)
    {
        return true;
    }

    return false;
}

public void resolveCollision(Ball ball)
{
    // get the mtd
    Vector2d delta = (position.subtract(ball.position));
    float d = delta.getLength();
    // minimum translation distance to push balls apart after intersecting
    Vector2d mtd = delta.multiply(((getRadius() + ball.getRadius())-d)/d); 


    // resolve intersection --
    // inverse mass quantities
    float im1 = 1 / getMass(); 
    float im2 = 1 / ball.getMass();

    // push-pull them apart based off their mass
    position = position.add(mtd.multiply(im1 / (im1 + im2)));
    ball.position = ball.position.subtract(mtd.multiply(im2 / (im1 + im2)));

    // impact speed
    Vector2d v = (this.velocity.subtract(ball.velocity));
    float vn = v.dot(mtd.normalize());

    // sphere intersecting but moving away from each other already
    if (vn > 0.0f) return;

    // collision impulse
    float i = (-(1.0f + Constants.restitution) * vn) / (im1 + im2);
    Vector2d impulse = mtd.multiply(i);

    // change in momentum
    this.velocity = this.velocity.add(impulse.multiply(im1));
    ball.velocity = ball.velocity.subtract(impulse.multiply(im2));

}

Code Source: Source complète pour ball to ball Collider.

Si quelqu'un a des suggestions pour améliorer ce simulateur de physique de base, faites-le moi savoir! Une chose que je dois encore ajouter est le moment angulaire afin que les balles roulent de manière plus réaliste. Toutes les autres suggestions? Laisser un commentaire!

248

collision-detection graphics language-agnostic physics

demandé sur mmcdole 2008-12-06 06:24:00

12 réponses

score 106 · Answer 1

Pour détecter si deux balles entrent en collision, il suffit de vérifier si la distance entre leurs centres est inférieure à deux fois le rayon. Pour faire une collision parfaitement élastique entre les balles, il suffit de s'inquiéter de la composante de la vitesse qui est dans le sens de la collision. L'autre composant (tangent à la collision) restera le même pour les deux balles. Vous pouvez obtenir les composants de collision en créant un vecteur unitaire pointant dans la direction d'une balle à l'autre, puis prendre le produit de point avec les vecteurs de vitesse des boules. Vous pouvez ensuite brancher ces composants dans une équation de collision 1D parfaitement élastique.

, Wikipédia a une assez bonne résumé de l'ensemble du processus. Pour les billes de toute masse, les nouvelles vitesses peuvent être calculées en utilisant les équations (où v1 et v2 sont les vitesses après la collision, et u1, u2 sont d'avant):

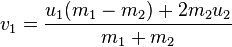
$v_{1} = \frac{u_{1}(m_{1}-m_{2})+2m_{2}u_{2}}{m_{1}+m_{2}}$

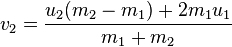
$v_{2} = \frac{u_{2}(m_{2}-m_{1})+2m_{1}u_{1}}{m_{1}+m_{2}}$

Si les billes ont la même masse alors les vitesses sont tout simplement changé. Voici un code que j'ai écrit qui fait quelque chose de similaire:

void Simulation::collide(Storage::Iterator a, Storage::Iterator b)
{
    // Check whether there actually was a collision
    if (a == b)
        return;

    Vector collision = a.position() - b.position();
    double distance = collision.length();
    if (distance == 0.0) {              // hack to avoid div by zero
        collision = Vector(1.0, 0.0);
        distance = 1.0;
    }
    if (distance > 1.0)
        return;

    // Get the components of the velocity vectors which are parallel to the collision.
    // The perpendicular component remains the same for both fish
    collision = collision / distance;
    double aci = a.velocity().dot(collision);
    double bci = b.velocity().dot(collision);

    // Solve for the new velocities using the 1-dimensional elastic collision equations.
    // Turns out it's really simple when the masses are the same.
    double acf = bci;
    double bcf = aci;

    // Replace the collision velocity components with the new ones
    a.velocity() += (acf - aci) * collision;
    b.velocity() += (bcf - bci) * collision;
}

En ce qui concerne l'efficacité, Ryan Fox a raison, vous devriez envisager de diviser la région en sections, puis de faire la détection de collision dans chaque section. Gardez à l'esprit que les balles peuvent entrer en collision avec d'autres boules à l'intérieur d'une section, ce qui peut rendre votre code plus compliqué. L'efficacité n'aura probablement pas d'importance jusqu'à ce que vous ayez plusieurs centaines de balles. Pour les points bonus, vous pouvez exécuter chaque section sur un noyau différent, ou diviser le traitement des collisions au sein de chaque section.

score 46 · Answer 2

Eh bien, il y a des années, j'ai fait le programme comme vous l'avez présenté ici.
Il y a un problème caché (ou plusieurs, dépend du point de vue):

Si la vitesse de la balle est trop haut, vous pouvez manquer la collision.

Et aussi, presque dans 100% des cas, vos nouvelles vitesses seront fausses. Eh bien, pas vitesses, mais positions. Vous devez calculer de nouvelles vitesses précisément au bon endroit. Sinon, vous venez de déplacer des balles sur une petite quantité "erreur", qui est disponible à partir de l'étape discrète précédente.

La solution est évidente: vous devez diviser le pas de temps de sorte que vous passez d'abord à la bonne place, puis vous entrez en collision, puis vous déplacez pour le reste du temps.

score 20 · Answer 3

Vous devez utiliser le partitionnement de l'espace pour résoudre ce problème.

Lire sur Partitionnement De L'Espace Binaire et Quadtrees

score 12 · Answer 4

Comme une clarification à la suggestion de Ryan Fox de diviser l'écran en régions, et de ne vérifier que les collisions dans les régions...

Par exemple, divisez l'aire de jeu en une grille de carrés (qui indiquera arbitrairement 1 unité de longueur par côté), et vérifiez les collisions dans chaque carré de la grille.

C'est absolument la bonne solution. Le seul problème avec cela (comme l'a souligné une autre affiche) est que les collisions au-delà des frontières sont un problème.

Le la solution consiste à superposer une deuxième grille à un décalage vertical et horizontal de 0,5 unité par rapport à la première.

Ensuite, toutes les collisions qui seraient à travers les limites dans la première grille (et donc non détectées) seront dans les carrés de la grille dans la deuxième grille. Tant que vous gardez une trace des collisions que vous avez déjà traitées (car il y a probablement un certain chevauchement), vous n'avez pas à vous soucier de la gestion des cas de bord. Toutes les collisions seront dans un carré de grille sur l'une des grilles.

score 10 · Answer 5

Un bon moyen de réduire le nombre de tests de collision est de diviser l'écran en différentes sections. Vous comparez alors seulement chaque balle aux balles dans la même section.

score 7 · Answer 6

Une chose que je vois ici pour optimiser.

Bien que je convienne que les balles frappent lorsque la distance est la somme de leurs rayons, il ne faut jamais réellement calculer cette distance! Au contraire, calculez-le carré et travaillez-le de cette façon. Il n'y a aucune raison pour cette opération de racine carrée coûteuse.

En outre, une fois que vous avez trouvé une collision, vous devez continuer à évaluer les collisions jusqu'à ce qu'il n'en reste plus. Le problème est que le premier pourrait causer d'autres qui doivent être résolus avant de vous faire une idée précise. Considérez ce qui se passe si la balle frappe une balle au bord? La deuxième balle frappe le bord et rebondit immédiatement dans la première balle. Si vous frappez dans un tas de balles dans le coin, vous pourriez avoir un certain nombre de collisions qui doivent être résolues avant de pouvoir itérer le cycle suivant.

En ce qui concerne le O (N^2), Tout ce que vous pouvez faire est de minimiser le coût de rejeter ceux qui manquent:

1) Une balle qui ne bouge pas ne peut rien frapper. Si il y a un nombre raisonnable de balles qui traînent sur le sol cela pourrait sauver beaucoup de tests. (Notez que vous devez toujours vérifier si quelque chose a frappé la balle stationnaire.)

2) quelque chose qui pourrait valoir la peine de faire: divisez l'écran en un certain nombre de zones mais les lignes doivent être floues-les boules au bord d'une zone sont répertoriées comme étant dans toutes les zones pertinentes (pourrait être 4). J'utiliserais une grille 4x4, stockerais les zones en bits. Si un et des zones de deux boules zones renvoie zéro, fin de test.

3) Comme je l'ai mentionné, ne faites pas la racine carrée.

score 6 · Answer 7

J'ai trouvé une excellente page avec des informations sur la détection de collision et la réponse en 2D.

Http://www.metanetsoftware.com/technique.html

Ils essaient d'expliquer comment cela se fait d'un point de vue académique. Ils commencent par la simple détection de collision d'objet à Objet, et passent à la réponse de collision et à la façon de la mettre à l'échelle.

Modifier: lien mis à jour

score 3 · Answer 8

Vous avez deux façons simples de le faire. Jay a couvert la façon précise de vérifier du centre de la balle.

Le moyen le plus simple est d'utiliser une boîte englobante rectangle, définir la taille de votre boîte à 80% de la taille de la balle, et vous simulerez la collision assez bien.

Ajoutez une méthode à votre classe de balle:

public Rectangle getBoundingRect()
{
   int ballHeight = (int)Ball.Height * 0.80f;
   int ballWidth = (int)Ball.Width * 0.80f;
   int x = Ball.X - ballWidth / 2;
   int y = Ball.Y - ballHeight / 2;

   return new Rectangle(x,y,ballHeight,ballWidth);
}

Ensuite, dans votre boucle:

// Checks every ball against every other ball. 
// For best results, split it into quadrants like Ryan suggested. 
// I didn't do that for simplicity here.
for (int i = 0; i < balls.count; i++)
{
    Rectangle r1 = balls[i].getBoundingRect();

    for (int k = 0; k < balls.count; k++)
    {

        if (balls[i] != balls[k])
        {
            Rectangle r2 = balls[k].getBoundingRect();

            if (r1.Intersects(r2))
            {
                 // balls[i] collided with balls[k]
            }
        }
    }
}

score 3 · Answer 9

Je le vois laissé entendre ici et là, mais vous pouvez également faire un calcul plus rapide en premier, comme comparer les boîtes englobantes pour le chevauchement, puis faire un chevauchement basé sur le rayon si ce premier test réussit.

Le calcul addition/différence est beaucoup plus rapide pour une boîte englobante que tout le trig pour le rayon, et la plupart du temps, le test de la boîte englobante écartera la possibilité d'une collision. Mais si vous testez à nouveau avec trig, vous obtenez les résultats précis que vous recherchez.

Oui, ce sont deux tests, mais ce sera globalement plus rapide.

score 3 · Answer 10

CE KineticModel est une implémentation de l'approche Citée en Java.

3

répondu trashgod 2011-09-02 17:29:59

score 2 · Answer 11

J'ai implémenté ce code en JavaScript en utilisant L'élément HTML Canvas, et il a produit de merveilleuses simulations à 60 images par seconde. J'ai commencé la simulation avec une collection d'une douzaine de balles à des positions et des vitesses aléatoires. J'ai trouvé qu'à des vitesses plus élevées, une collision entre une petite balle et une balle beaucoup plus grande faisait que la petite balle semblait Coller au bord de la balle plus grande, et se déplaçait à environ 90 degrés autour de la balle plus grande avant de se séparer. (Je me demande si quelqu'un d'autre a observé ce comportement.)

Une journalisation des calculs a montré que la Distance de Translation minimale dans ces cas n'était pas assez grande pour empêcher les mêmes billes de se heurter à l'étape de temps suivante. J'ai fait quelques expériences et j'ai trouvé que je pouvais résoudre ce problème en augmentant la MTD en fonction des vitesses relatives:

dot_velocity = ball_1.velocity.dot(ball_2.velocity);
mtd_factor = 1. + 0.5 * Math.abs(dot_velocity * Math.sin(collision_angle));
mtd.multplyScalar(mtd_factor);

J'ai vérifié avant et après cette correction, l'énergie cinétique totale est conservée pour chaque collision. 0,5 la valeur dans mtd_factor était approximativement la valeur minimale trouvée pour toujours séparer les billes après une collision.

Bien que ce correctif introduit une petite quantité d'erreur dans la physique exacte du système, le compromis est que maintenant des balles très rapides peuvent être simulées dans un navigateur sans diminuer la taille du Pas de temps.

score 2 · Answer 12

Comme je le vois ici, une meilleure façon de l'implémenter n'est pas mentionnée. 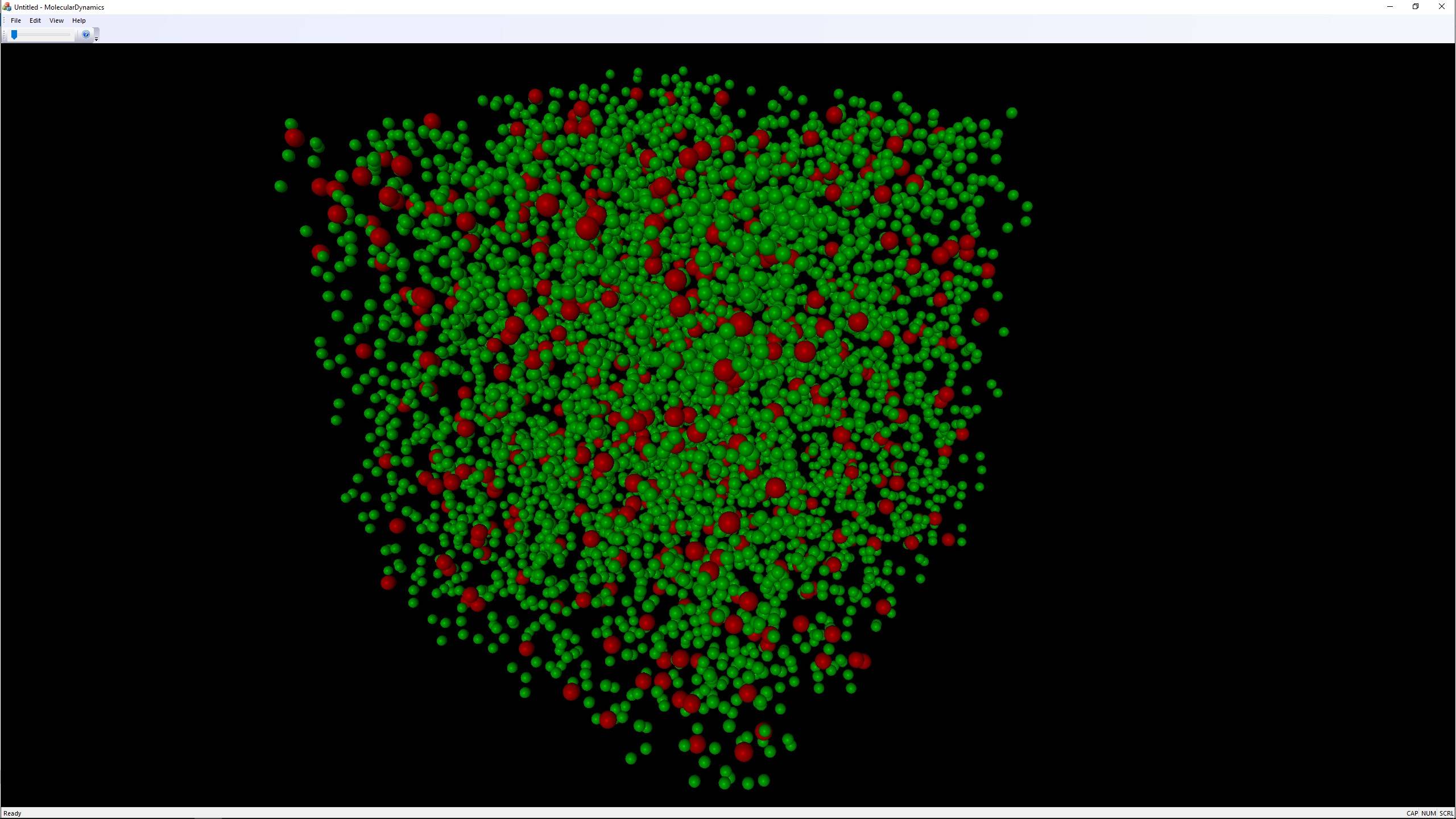je vous renvoie à "comment simuler le billard et les systèmes similaires" de Boris D. Lubachevsky, disponible sur arxiv: http://arxiv.org/abs/cond-mat/0503627 dans l'image ci-jointe est une capture d'écran d'un programme que j'ai l'intention de faire open source quand je vais le terminer. Même à un stade précoce est en cours d'exécution avec 5000 sphères assez bien. J'espère faire encore mieux même si Je ne veux pas implémenter la sectorisation, Je vous voulez garder le code facile à comprendre. La description sera disponible sur http://compphys.go.ro

Plus Tard edit: Le code est maintenant disponible sur GitHub: https://github.com/aromanro/EventMolecularDynamics Description est sur le blog: http://compphys.go.ro/event-driven-molecular-dynamics/

Las etiquetas más populares

Collision balle à balle-détection et manipulation

Succès!

12 réponses