Zone d'intersection entre le cercle et le rectangle

j'espère que ce n'est pas une mauvaise forme de poster une réponse à une si vieille question. J'ai regardé au-dessus des solutions ci-dessus et ai travaillé sur un algorithme qui est similaire à Daniels première réponse, mais un bon peu plus serré.

en résumé, supposons que toute la surface soit dans le rectangle, soustrayez les quatre segments dans les demi-plans externes, puis ajoutez les zones dans les quatre quadrants externes, en écartant les cas triviaux le long du chemin.

pseudo-code est seulement ~12 lignes..)

find the signed (negative out) normalized distance from the circle center
to each of the infinitely extended rectangle edge lines,
ie.
d_1=(xcenter-xleft)/r
d_2=(ycenter-ybottom)/r
etc

for convenience order 1,2,3,4 around the edge. If the rectangle is not
aligned with the cartesian coordinates this step is more complicated but
the remainder of the algorithm is the same

If ANY d_i <=- 1 return 0

if ALL d_i >=  1 return Pi r^2

this leave only one remaining fully outside case: circle center in
an external quadrant, and distance to corner greater than circle radius:

for each adjacent i,j (ie. i,j=1,2;2,3;3,4;4,1)
     if d_i<=0 and d_j <= 0 and d_i^2+d_j^2 > 1 return 0

now begin with full circle area  and subtract any areas in the
four external half planes

Area= Pi r^2
for each  d_i>-1
     a_i=arcsin( d_i )  #save a_i for next step
     Area -= r^2/2 (Pi - 2 a_i - sin(2 a_i)) 

At this point note we have double counted areas in the four external
quadrants, so add back in:

for each adjacent i,j
   if  d_i < 1 and   d_j < 1  and d_i^2+d_j^2 < 1
       Area += r^2/4 (Pi- 2 a_i - 2 a_j -sin(2 a_i) -sin(2 a_j) + 4 sin(a_i) sin(a_j))

return Area

incidemment, cette dernière formule pour la surface d'un cercle contenue dans un quadrant plan est facilement dérivée comme la somme d'un segment circulaire, de deux triangles droits et d'un rectangle.

de Profiter de.

je me rends compte qu'on m'a répondu il y a un certain temps, mais je résous le même problème et je n'ai pas pu trouver une solution pratique que je pourrais utiliser. Notez que mes cases sont aligné sur l'axe , ce qui n'est pas tout à fait spécifié par L'OP. La solution ci-dessous est complètement générale, et fonctionnera pour n'importe quel nombre d'intersections (pas seulement deux). Notez que si vos boîtes ne sont pas alignées sur l'axe (mais toujours des boîtes à angle droit, plutôt que des boîtes générales "1519280920 quads ), vous pouvez profiter des cercles étant ronds, tourner les coordonnées de tout pour que la boîte se retrouve alignée sur l'axe et puis utilisez ce code.

je veux utiliser l'intégration - qui semble être une bonne idée. Commençons par écrire une formule évidente pour tracer un cercle:

x = center.x + cos(theta) * radius
y = center.y + sin(theta) * radius

^
|
|**###        **
| #*  #      *          * x
|#  *  #    *           # y
|#  *  #    *     
+-----------------------> theta
     *  #  *  # 
     *  #  *  #
      *  #*  #
       ***###

c'est bien, mais je suis incapable d'intégrer la zone de ce cercle au-dessus de x ou y ; ceux-ci sont différentes quantités. Je ne peux intégrer que sur l'angle theta , donnant des zones de tranches de pizza. Pas ce que je veux. Essayons de changer les arguments:

(x - center.x) / radius = cos(theta) // the 1st equation
theta = acos((x - center.x) / radius) // value of theta from the 1st equation
y = center.y + sin(acos((x - center.x) / radius)) * radius // substitute to the 2nd equation

c'est plus comme ça. Maintenant, étant donné la portée de x , je peux intégrer plus de y , pour obtenir une zone de la moitié supérieure d'un cercle. Cela ne vaut que pour x dans [center.x - radius, center.x + radius] (d'autres valeurs provoqueront des sorties imaginaires) mais nous savons que la zone en dehors de cette plage est nulle, donc qui est manipulé facilement. Supposons unit circle pour la simplicité, nous pouvons toujours brancher le centre et le rayon de retour plus tard:

y = sin(acos(x)) // x in [-1, 1]
y = sqrt(1 - x * x) // the same thing, arguably faster to compute http://www.wolframalpha.com/input/?i=sin%28acos%28x%29%29+

               ^ y
               |
            ***|***     <- 1
        ****   |   ****
      **       |       **
     *         |         *
    *          |          *
----|----------+----------|-----> x
   -1                     1

cette fonction a en effet une intégrale de pi/2 , puisqu'il s'agit d'une moitié supérieure d'un cercle unitaire (l'aire d'un demi-cercle est pi * r^2 / 2 et nous avons déjà dit unité , qui signifie r = 1 ). Maintenant nous pouvons calculer la zone d'intersection d'un demi-cercle et d'une boîte infiniment haute, debout sur le x axe (le centre du cercle se trouve également sur l'axe des x) en intégrant plus de y :

f(x): integral(sqrt(1 - x * x) * dx) = (sqrt(1 - x * x) * x + asin(x)) / 2 + C // http://www.wolframalpha.com/input/?i=sqrt%281+-+x*x%29
area(x0, x1) = f(max(-1, min(1, x1))) - f(max(-1, min(1, x0))) // the integral is not defined outside [-1, 1] but we want it to be zero out there

        ~         ~
        |      ^  |
        |      |  |
        |   ***|***     <- 1
        ****###|##|****
      **|######|##|    **
     *  |######|##|      *
    *   |######|##|       *
----|---|------+--|-------|-----> x
   -1   x0        x1      1

cela peut ne pas être très utile, car les boîtes infiniment hautes ne sont pas ce que nous voulons. Nous avons besoin d'ajouter un paramètre supplémentaire pour pouvoir libérer le bord inférieur de la boîte infiniment haute:

g(x, h): integral((sqrt(1 - x * x) - h) * dx) = (sqrt(1 - x * x) * x + asin(x) - 2 * h * x) / 2 + C // http://www.wolframalpha.com/input/?i=sqrt%281+-+x*x%29+-+h
area(x0, x1, h) = g(min(section(h), max(-section(h), x1))) - g(min(section(h), max(-section(h), x0)))

        ~         ~
        |      ^  |
        |      |  |
        |   ***|***     <- 1
        ****###|##|****
      **|######|##|    **
     *  +------+--+      *   <- h
    *          |          *
----|---|------+--|-------|-----> x
   -1   x0        x1      1

où h est la distance (positive) du bord inférieur de notre boîte infinie par rapport à l'axe des X. La fonction section calcule la position (positive) d'intersection du cercle de l'unité avec la ligne horizontale donnée par y = h et nous pourrions la définir en résolvant:

sqrt(1 - x * x) = h // http://www.wolframalpha.com/input/?i=sqrt%281+-+x+*+x%29+%3D+h
section(h): (h < 1)? sqrt(1 - h * h) : 0 // if h is 1 or above, then the section is an empty interval and we want the area integral to be zero

               ^ y
               |  
            ***|***     <- 1
        ****   |   ****  
      **       |       **
-----*---------+---------*------- y = h
    *          |          *
----||---------+---------||-----> x
   -1|                   |1
-section(h)          section(h)

maintenant nous pouvons faire bouger les choses. Ainsi, comment calculer la zone d'intersection d'une boîte finie intersectant un cercle d'unité au-dessus de l'axe des x:

area(x0, x1, y0, y1) = area(x0, x1, y0) - area(x0, x1, y1) // where x0 <= x1 and y0 <= y1

        ~         ~                              ~         ~
        |      ^  |                              |      ^  |
        |      |  |                              |      |  |
        |   ***|***                              |   ***|*** 
        ****###|##|****                          ****---+--+****      <- y1
      **|######|##|    **                      **       |       **
     *  +------+--+      *   <- y0            *         |         *
    *          |          *                  *          |          *
----|---|------+--|-------|-----> x      ----|---|------+--|-------|-----> x
        x0        x1                             x0        x1


               ^
               |
            ***|***
        ****---+--+****      <- y1
      **|######|##|    **
     *  +------+--+      *   <- y0
    *          |          *
----|---|------+--|-------|-----> x
        x0        x1

c'est bien. Alors pourquoi pas une boîte qui n'est pas au-dessus de l'axe x? Je dirais que toutes les boîtes ne le sont pas. Trois cas simples se lève:

• la case est au-dessus de l'axe des x (utilisez l'équation ci-dessus)
• la case est sous l'axe des x (inversez le signe des coordonnées y et utilisez l'équation ci-dessus)
• la boîte croise l'axe des abscisses (diviser la boîte en moitié supérieure et moitié inférieure, calculer la superficie des deux en utilisant les valeurs ci-dessus et les additionner)

C'est assez facile? Ecrivons un peu de code:

float section(float h, float r = 1) // returns the positive root of intersection of line y = h with circle centered at the origin and radius r
{
    assert(r >= 0); // assume r is positive, leads to some simplifications in the formula below (can factor out r from the square root)
    return (h < r)? sqrt(r * r - h * h) : 0; // http://www.wolframalpha.com/input/?i=r+*+sin%28acos%28x+%2F+r%29%29+%3D+h
}

float g(float x, float h, float r = 1) // indefinite integral of circle segment
{
    return .5f * (sqrt(1 - x * x / (r * r)) * x * r + r * r * asin(x / r) - 2 * h * x); // http://www.wolframalpha.com/input/?i=r+*+sin%28acos%28x+%2F+r%29%29+-+h
}

float area(float x0, float x1, float h, float r) // area of intersection of an infinitely tall box with left edge at x0, right edge at x1, bottom edge at h and top edge at infinity, with circle centered at the origin with radius r
{
    if(x0 > x1)
        std::swap(x0, x1); // this must be sorted otherwise we get negative area
    float s = section(h, r);
    return g(max(-s, min(s, x1)), h, r) - g(max(-s, min(s, x0)), h, r); // integrate the area
}

float area(float x0, float x1, float y0, float y1, float r) // area of the intersection of a finite box with a circle centered at the origin with radius r
{
    if(y0 > y1)
        std::swap(y0, y1); // this will simplify the reasoning
    if(y0 < 0) {
        if(y1 < 0)
            return area(x0, x1, -y0, -y1, r); // the box is completely under, just flip it above and try again
        else
            return area(x0, x1, 0, -y0, r) + area(x0, x1, 0, y1, r); // the box is both above and below, divide it to two boxes and go again
    } else {
        assert(y1 >= 0); // y0 >= 0, which means that y1 >= 0 also (y1 >= y0) because of the swap at the beginning
        return area(x0, x1, y0, r) - area(x0, x1, y1, r); // area of the lower box minus area of the higher box
    }
}

float area(float x0, float x1, float y0, float y1, float cx, float cy, float r) // area of the intersection of a general box with a general circle
{
    x0 -= cx; x1 -= cx;
    y0 -= cy; y1 -= cy;
    // get rid of the circle center

    return area(x0, x1, y0, y1, r);
}

et quelques essais unitaires de base:

printf("%f\n", area(-10, 10, -10, 10, 0, 0, 1)); // unit circle completely inside a huge box, area of intersection is pi
printf("%f\n", area(-10, 0, -10, 10, 0, 0, 1)); // half of unit circle inside a large box, area of intersection is pi/2
printf("%f\n", area(0, 10, -10, 10, 0, 0, 1)); // half of unit circle inside a large box, area of intersection is pi/2
printf("%f\n", area(-10, 10, -10, 0, 0, 0, 1)); // half of unit circle inside a large box, area of intersection is pi/2
printf("%f\n", area(-10, 10, 0, 10, 0, 0, 1)); // half of unit circle inside a large box, area of intersection is pi/2
printf("%f\n", area(0, 1, 0, 1, 0, 0, 1)); // unit box covering one quadrant of the circle, area of intersection is pi/4
printf("%f\n", area(0, -1, 0, 1, 0, 0, 1)); // unit box covering one quadrant of the circle, area of intersection is pi/4
printf("%f\n", area(0, -1, 0, -1, 0, 0, 1)); // unit box covering one quadrant of the circle, area of intersection is pi/4
printf("%f\n", area(0, 1, 0, -1, 0, 0, 1)); // unit box covering one quadrant of the circle, area of intersection is pi/4
printf("%f\n", area(-.5f, .5f, -.5f, .5f, 0, 0, 10)); // unit box completely inside a huge circle, area of intersection is 1
printf("%f\n", area(-20, -10, -10, 10, 0, 0, 1)); // huge box completely outside a circle (left), area of intersection is 0
printf("%f\n", area(10, 20, -10, 10, 0, 0, 1)); // huge box completely outside a circle (right), area of intersection is 0
printf("%f\n", area(-10, 10, -20, -10, 0, 0, 1)); // huge box completely outside a circle (below), area of intersection is 0
printf("%f\n", area(-10, 10, 10, 20, 0, 0, 1)); // huge box completely outside a circle (above), area of intersection is 0

la sortie de ceci est:

3.141593
1.570796
1.570796
1.570796
1.570796
0.785398
0.785398
0.785398
0.785398
1.000000
-0.000000
0.000000
0.000000
0.000000

ce qui me semble correct. Vous pouvez inline fonctions si vous n'avez pas confiance en votre compilateur pour le faire pour vous.

cela utilise 6 sqrt, 4 asin, 8 div, 16 mul et 17 adds pour les boîtes qui ne croisent pas l'axe x et un double de cela (et 1 add) pour les boîtes qui font. Notez que les divisions sont par rayon et pourraient être réduit à deux divisions et un tas de multiplications. Si la case en question a coupé l'axe x mais n'a pas coupé l'axe y, Vous pouvez tourner tout par pi/2 et faire le calcul dans le coût original.

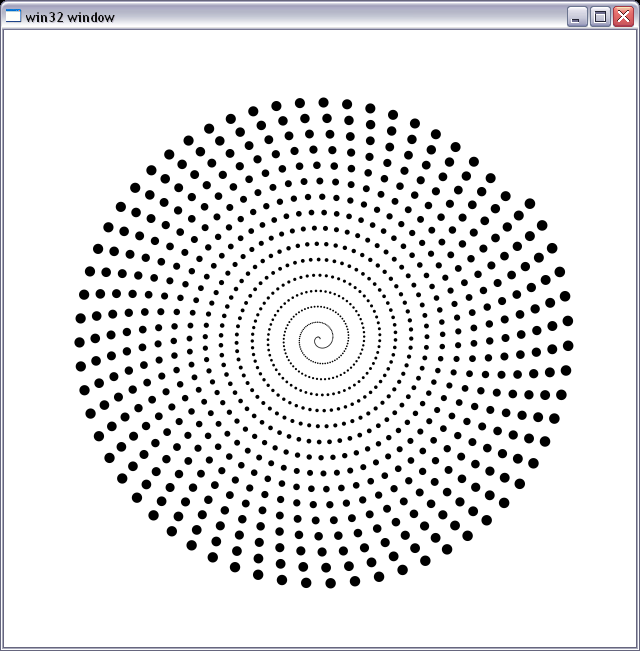
Je l'utilise comme référence pour déboguer le Circle rasterizer antialiasé de précision subpixel. Il est lent comme l'enfer :), j'ai besoin de calculer l'aire d'intersection de chaque pixel de la zone de délimitation du cercle avec le cercle pour obtenir de l'alpha. Vous pouvez je vois que ça marche et qu'aucun artefact numérique ne semble apparaître. La figure ci-dessous est le tracé d'un tas de cercles dont le rayon augmente de 0,3 px à environ 6 px, disposés en spirale.

voici comment calculer la zone de chevauchement entre le cercle et le rectangle où le centre du cercle se trouve à l'extérieur du rectangle. D'autres cas peuvent être réduits à ce problème.

la zone peut être calculée en intégrant l'équation circulaire y = sqrt[a^2 - (x-h)^2] + k où a est le rayon, (h,k) est le centre du cercle, pour trouver la zone sous la courbe. Vous pouvez utiliser l'intégration informatique où la zone est divisée en de nombreux petits rectangles et le calcul de la somme d'entre eux, ou tout simplement fermée.

et voici un c# source mettant en œuvre le concept ci-dessus. Notez qu'il existe un cas particulier où le x est à l'extérieur des limites du cercle. Je viens d'utiliser une solution de contournement simple ici (ce qui n'est pas de produire les réponses correctes dans tous les cas)

public static void RunSnippet()
{
    // test code
    double a,h,k,x1,x2;
    a = 10;
    h = 4;
    k = 0;
    x1 = -100;
    x2 = 100;

    double r1 = Integrate(x1, a, h, k);
    double r2 = Integrate(x2, a, h, k);

    Console.WriteLine(r2 - r1);

}

private static double Integrate(double x, double a,double h, double k)
{
    double a0 = a*a - (h-x)*(h-x);

    if(a0 <= 0.0){
        if(k == 0.0)
            return Math.PI * a * a / 4.0 * Math.Sign(x);
        else
            throw new Exception("outside boundaries");
    }

    double a1 = Math.Sqrt(a*a - (h-x)*(h-x)) * (h-x);
    double area = 0.5 * Math.Atan(a1 / ((h-x)*(h-x) - a*a))*a*a - 0.5 * a1 + k * x;
    return area;
}

Note: ce problème est très similaire à un dans Google Code Jam 2008 Qualification round problème: voler Swatter . Vous pouvez aussi cliquer sur les liens score pour télécharger le code source de la solution.

Merci pour les réponses,

j'ai oublié de mentionner que les estimations de superficie étaient suffisantes. C'est pourquoi, après avoir examiné toutes les options, j'ai opté pour l'estimation monte-carlo, où je générais des points aléatoires dans le cercle et vérifiais s'ils étaient dans la boîte.

Dans mon cas, c'est probablement plus performant. (J'ai une grille placée sur le cercle et j'ai pour mesurer le rapport du cercle appartenant à chacune des mailles. )

Merci

peut-être vous pouvez utiliser la réponse à cette question , où la zone d'intersection entre un cercle et un triangle est demandé. Séparez votre rectangle en deux triangles et utilisez les algorithmes qui y sont décrits.

une autre façon est de tracer une ligne entre les deux points d'intersection, ce qui divise votre zone dans un polygone (3 ou 4 bords) et un segment circulaire , pour les deux vous devriez être en mesure de trouver des bibliothèques plus facile ou faire le calcul vous-même.

Voici une autre solution pour le problème:

public static bool IsIntersected(PointF circle, float radius, RectangleF rectangle)
{

        var rectangleCenter = new PointF((rectangle.X +  rectangle.Width / 2),
                                         (rectangle.Y + rectangle.Height / 2));

        var w = rectangle.Width  / 2;
        var h = rectangle.Height / 2;

        var dx = Math.Abs(circle.X - rectangleCenter.X);
        var dy = Math.Abs(circle.Y - rectangleCenter.Y);

        if (dx > (radius + w) || dy > (radius + h)) return false;


        var circleDistance = new PointF
                                 {
                                     X = Math.Abs(circle.X - rectangle.X - w),
                                     Y = Math.Abs(circle.Y - rectangle.Y - h)
                                 };


        if (circleDistance.X <= (w))
        {
            return true;
        }

        if (circleDistance.Y <= (h))
        {
            return true;
        }

        var cornerDistanceSq = Math.Pow(circleDistance.X - w, 2) + 
                    Math.Pow(circleDistance.Y - h, 2);

        return (cornerDistanceSq <= (Math.Pow(radius, 2)));
}