Angle entre deux vecteurs en R

Ma réponse se compose de deux parties. La partie 1 est le calcul - pour donner de la clarté à tous les lecteurs du fil et pour rendre le code R qui suit compréhensible. La partie 2 est la programmation R.

Partie 1-Mathématiques

le produit dot de deux vecteurs x et o peut être défini comme suit:

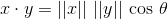
|| x / / est la norme euclidienne (également connue sous le nom de L₂ norme) de la vecteur x.

en manipulant la définition du produit dot, on peut obtenir:

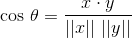
où theta est l'angle entre les vecteurs x et o exprimé en radians. Notez que thêta peut prendre une valeur qui se trouve sur l'intervalle fermé de 0 à pi.

en résolvant pour thêta elle-même, nous obtenons:

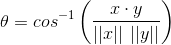
Partie 2-R Code

pour traduire les mathématiques en code R, Nous avons besoin de savoir comment effectuer deux calculs de matrice (vecteur); dot produit et norme euclidienne (qui est un type spécifique de norme, connu sous le nom de L₂ norme). Il faut aussi connaître L'équivalent R de la fonction cosinus inverse, cos ^-1.

à partir du début. Par référence à %*% opérateur. Avec référence à ?norm, le norm() retour de la fonction (paquet de base) norme d'un vecteur. La norme d'intérêt ici est le L₂ norm ou, dans le jargon de la documentation d'aide R, la norme "spectrale" ou "2". Cela signifie que l' type argument norm() fonction doit être égale à "2". Enfin, la fonction cosinus inverse de R est représentée par acos() fonction.

Solution

dotée à la fois des fonctions mathématiques et des fonctions R correspondantes, une fonction prototype (c'est - à - dire qui n'est pas une norme de production) peut être mise en place-en utilisant des fonctions de Base package-comme indiqué ci-dessous. Si l'information ci-dessus a un sens, alors le angle() la fonction qui suit doit être clair, sans autre commentaire.

angle <- function(x,y){
  dot.prod <- x%*%y 
  norm.x <- norm(x,type="2")
  norm.y <- norm(y,type="2")
  theta <- acos(dot.prod / (norm.x * norm.y))
  as.numeric(theta)
}

tester la fonction

un test pour vérifier que le la fonction fonctionne. Laissez x = (2,1) et o = (1,2). Produit scalaire entre x et o est 4. Norme euclidienne de x sqrt(5). Norme euclidienne de o est également sqrt(5). cos theta = 4/5. Thêta est d'environ 0,643 radians.

x <- as.matrix(c(2,1))
y <- as.matrix(c(1,2))
angle(t(x),y)          # Use of transpose to make vectors (matrices) conformable.
[1] 0.6435011

j'espère que cela aide!

pour les vecteurs 2D, la façon indiquée dans la réponse acceptée et les autres ne tient pas compte de l'orientation (le signe) de l'angle (angle(M,N) est le même que angle(N,M)) et elle renvoie une valeur correcte pour un angle entre 0 et pi.

atan2 fonction permettant d'obtenir un angle orienté et une valeur correcte (modulo 2pi).

angle <- function(M,N){
  acos( sum(M*N) / ( sqrt(sum(M*M)) * sqrt(sum(N*N)) ) )
}
angle2 <- function(M,N){
  atan2(N[2],N[1]) - atan2(M[2],M[1]) 
}

Vérifiez que angle2 donne la valeur correcte:

> theta <- seq(-2*pi, 2*pi, length.out=10)
> O <- c(1,0)
> test1 <- sapply(theta, function(theta) angle(M=O, N=c(cos(theta),sin(theta))))
> all.equal(test1 %% (2*pi), theta %% (2*pi))
[1] "Mean relative difference: 1"
> test2 <- sapply(theta, function(theta) angle2(M=O, N=c(cos(theta),sin(theta))))
> all.equal(test2 %% (2*pi), theta %% (2*pi))
[1] TRUE

Vous devez utiliser le produit scalaire. Disons que vous avez V փ = ( x₁, o₁, z₁) et V փ = ( x₂, o₂, zo₂ + zo փ+ z

et vous avez juste besoin de la fonction arccos (ou cosine inverse) appliquée à cos( θ) pour obtenir l'angle.