Algorithme pour identifier un polyomino (ou un hash polyomino) libre unique)
En bref: comment hacher un polyomino gratuit?
ceci pourrait être généralisé en: comment hacher efficacement une collection arbitraire de coordonnées entières 2D, où un ensemble contient des paires uniques d'entiers non négatifs, et un ensemble est considéré comme unique si et seulement si aucune traduction, rotation ou retournement ne peut le mapper de façon identique à un autre ensemble?
pour les lecteurs impatients, s'il vous plaît noter que je suis pleinement conscient d'une approche de la force brute. Je suis à la recherche d'un ou une preuve très convaincante qu'aucune autre voie ne peut exister.
je travaille sur des algorithmes différents pour générer random polyominos. Je veux tester leur sortie pour déterminer comment aléatoire qu'ils sont, c'est à dire certains cas d'un ordre donné généré plus fréquemment que d'autres. Visuellement, il est très facile d'identifier les différentes orientations d'un polyomino libre, par exemple L'illustration suivante de Wikipedia montre les 8 orientations de le" F " pentomino ( Source):
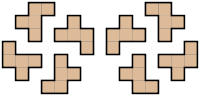
comment mettre un nombre sur ce polyomino - c'est-à-dire hacher un polyomino libre? Je ne veux pas dépendre d'une liste pré-colulée de polyominos "nommés". Les noms largement acceptés n'existent que pour les commandes 4 et 5, de toute façon.
ceci n'est pas nécessairement équivalent à énumérer tous les polyominos libres (ou unilatéraux, ou fixes) d'un ordre donné. Je ne veux compter que le nombre de fois la configuration apparaît. Si un algorithme générateur ne produit jamais un certain polyomino, il ne sera tout simplement pas compté.
La logique de base du comptage est:
testcount = 10000 // Arbitrary
order = 6 // Create hexominos in this test
hashcounts = new hashtable
for i = 1 to testcount
poly = GenerateRandomPolyomino(order)
hash = PolyHash(poly)
if hashcounts.contains(hash) then
hashcounts[hash]++
else
hashcounts[hash] = 1
Ce que je cherche est un moyen efficace PolyHash algorithme. Les polyominos d'entrée sont simplement définis comme un ensemble de coordonnées. Une orientation du t tetronimo pourrait être, par exemple:
[[1,0], [0,1], [1,1], [2,1]]:
|012
-+---
0| X
1|XXX
vous pouvez supposer que ce polyomino d'entrée sera déjà normalisé pour être aligné avec le X et des axes Y et n'ont que des coordonnées positives. Formellement, chaque ensemble:
- aura au moins 1 coordonnée où la valeur de x est 0
- aura au moins 1 coordonnée où la valeur y est 0
- n'Aura pas de coordonnées où x < 0 ou y < 0
je suis vraiment à la recherche de nouveaux algorithmes qui évitent le nombre croissant d'opérations entières requises par une approche de force brute générale, décrite ci-dessous.
Brute force
Une attaque par force brute solution proposée ici et ici consiste à Hasher chaque jeu comme un entier non signé en utilisant chaque coordonnée comme un drapeau binaire, et de prendre le hachage minimum de toutes les rotations possibles (et dans mon cas flips), où chaque rotation / flip doit également être traduit à l'origine. Il en résulte un total de 23 opérations de jeu pour chaque jeu d'entrée pour obtenir le " free" hash:
- Rotation (6x)
- Flip (1x)
- Translate (7x)
- Hash (8x)
- Trouver le minimum de valeurs de hachage calculées (1x)
où la séquence des opérations pour obtenir chaque hachage est:
- Hash
- Faire Pivoter, De Traduire, De Hachage
- Faire Pivoter, De Traduire, De Hachage
- Faire Pivoter, De Traduire, De Hachage
- Flip, De Traduire, De Hachage
- Rotation, De Traduire, De Hachage
- Faire Pivoter, De Traduire, De Hachage
- Faire Pivoter, De Traduire, De Hachage
6 réponses
Eh bien, j'ai trouvé une approche complètement différente. (Merci également à corsiKa pour ses précieux conseils!) Au lieu de Hasher / encoder les carrés, coder le chemin. Le chemin consiste en une séquence de 'virages' (sans virage) à effectuer avant de dessiner chaque segment d'unité. Je pense qu'un algorithme pour obtenir le chemin à partir des coordonnées des carrés est en dehors de la portée de cette question.
Cela fait quelque chose de très important: il détruit toutes les informations sur l'emplacement et l'orientation, dont nous n'avons pas besoin. Il est également très facile d'obtenir le chemin d'accès de l'objet retourné: vous le faites, il suffit d'inverser l'ordre des éléments. Le stockage est compact car chaque élément ne nécessite que 2 bits.
Il n'introduire une contrainte supplémentaire: le polyomino ne doit pas avoir de trous complètement fermés. (Formellement, cela doit être simplement connecté.) La plupart des discussions de polyominos considèrent un trou pour exister même si elle est scellée seulement par deux coins touchant, car cela empêche carrelage avec tout autre polyomino non-trivial. Le tracé des bords n'est pas gêné par le fait de toucher les coins (comme dans le simple heptomino avec un trou), mais il ne peut pas sauter d'une boucle externe à l'intérieur comme à l'complètes en forme d'anneau octomino:
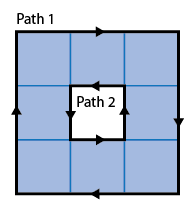
il produit aussi un défi supplémentaire: trouver l'ordre minumum de la boucle de chemin encodée. C'est parce que toute rotation du chemin (au sens de rotation de la chaîne) est un encodage valide. Pour avoir toujours l' encodage nous devons trouver la rotation minimale (ou maximale) des instructions de chemin. Heureusement, ce problème a déjà été résolu: voir, par exemple,http://en.wikipedia.org/wiki/Lexicographically_minimal_string_rotation.
Exemple:
si nous assignons arbitrairement les valeurs suivantes au mouvement opérations:
- Pas de tour: 1
- tourner à droite: 2
- tourner à gauche: 3
voici le F pentomino tracé dans le sens des aiguilles d'une montre:
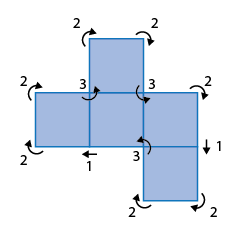
un encodage initial arbitraire pour le F pentomino est (à partir du coin en bas à droite):
2,2,3,1,2,2,3,2,2,3,2,1
la rotation minimale résultante de l'encodage est
1,2,2,3,1,2,2,3,2,2,3,2
avec 12 éléments, cette boucle peut être emballée en 24 bits si deux les bits sont utilisés par instruction ou seulement 19 bits si les instructions sont encodées comme des puissances de trois. Même avec l'encodage de l'élément 2-bit peut facilement s'Adapter que dans un seul entier 32 bits non signé 0x6B6BAE:
1- 2- 2- 3- 1- 2- 2- 3- 2- 2- 3- 2
= 01-10-10-11-01-10-10-11-10-10-11-10
= 00000000011010110110101110101110
= 0x006B6BAE
l'encodage de base-3 avec le début de la boucle dans les puissances les plus significatives de 3 est 0x5795F:
1*3^11 + 2*3^10 + 2*3^9 + 3*3^8 + 1*3^7 + 2*3^6
+ 2*3^5 + 3*3^4 + 2*3^3 + 2*3^2 + 3*3^1 + 2*3^0
= 0x0005795F
le nombre maximum de vertex dans le chemin autour d'un polyomino d'ordre n2n + 2. Pour les 2 bits codant le nombre de bits est le double de la nombre de mouvements, donc le nombre maximum de bits nécessaires est 4n + 4. Pour l'encodage de base-3 c'est:
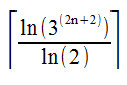
où la "potence" est la fonction de plafond. En conséquence n'importe quel polyomino jusqu'à l'ordre 9 peut être encodé dans un seul entier de 32 bits. Sachant cela, vous pouvez choisir votre structure de données spécifique à la plate-forme en conséquence pour la comparaison la plus rapide de hachage étant donné l'ordre maximum des polyominos que vous serez hachage.
Vous pouvez le réduire à 8 opérations de hachage sans avoir à retourner, faire pivoter, ou re-traduire.
notez que cet algorithme suppose que vous travaillez avec des coordonnées relatives à lui-même. C'est-à-dire qu'il n'est pas dans la nature.
au lieu d'appliquer des opérations qui tournent, tournent et traduisent, il suffit de changer l'ordre dans lequel vous Hachez.
Par exemple, prenons le F pent ci-dessus. Dans l'exemple simple, supposons le hachage l'opération a été quelque chose comme ceci:
int hashPolySingle(Poly p)
int hash = 0
for x = 0 to p.width
fory = 0 to p.height
hash = hash * 31 + p.contains(x,y) ? 1 : 0
hashPolySingle = hash
int hashPoly(Poly p)
int hash = hashPolySingle(p)
p.rotateClockwise() // assume it translates inside
hash = hash * 31 + hashPolySingle(p)
// keep rotating for all 4 oritentations
p.flip()
// hash those 4
au lieu d'appliquer la fonction AUX 8 différentes orientations du poly, j'appliquerais 8 différentes fonctions de hachage à 1 poly.
int hashPolySingle(Poly p, bool flip, int corner)
int hash = 0
int xstart, xstop, ystart, ystop
bool yfirst
switch(corner)
case 1: xstart = 0
xstop = p.width
ystart = 0
ystop = p.height
yfirst = false
break
case 2: xstart = p.width
xstop = 0
ystart = 0
ystop = p.height
yfirst = true
break
case 3: xstart = p.width
xstop = 0
ystart = p.height
ystop = 0
yfirst = false
break
case 4: xstart = 0
xstop = p.width
ystart = p.height
ystop = 0
yfirst = true
break
default: error()
if(flip) swap(xstart, xstop)
if(flip) swap(ystart, ystop)
if(yfirst)
for y = ystart to ystop
for x = xstart to xstop
hash = hash * 31 + p.contains(x,y) ? 1 : 0
else
for x = xstart to xstop
for y = ystart to ystop
hash = hash * 31 + p.contains(x,y) ? 1 : 0
hashPolySingle = hash
qui est alors appelé de 8 façons différentes. Vous pouvez également encapsuler hashPolySingle in pour boucle autour du coin, et autour du flip ou non. Tout de même.
int hashPoly(Poly p)
// approach from each of the 4 corners
int hash = hashPolySingle(p, false, 1)
hash = hash * 31 + hashPolySingle(p, false, 2)
hash = hash * 31 + hashPolySingle(p, false, 3)
hash = hash * 31 + hashPolySingle(p, false, 4)
// flip it
hash = hash * 31 + hashPolySingle(p, true, 1)
hash = hash * 31 + hashPolySingle(p, true, 2)
hash = hash * 31 + hashPolySingle(p, true, 3)
hash = hash * 31 + hashPolySingle(p, true, 4)
hashPoly = hash
de cette façon, vous tournez implicitement le poly de chaque direction, mais vous n'êtes pas en fait effectuer la rotation et la traduction. Il effectue les 8 hashs, qui semblent être entièrement nécessaires afin de Hasher avec précision toutes les 8 orientations, mais ne gaspille pas les passages au-dessus du poly qui ne font pas réellement les hashs. Cela me semble être la solution la plus élégante.
notez qu'il peut y avoir un meilleur algorithme hashPolySingle() à utiliser. Le mien utilise un algorithme D'épuisement cartésien qui est de l'ordre de O(n^2). Son pire scénario est une forme en L, qui provoquer un N/2 * (N-1)/2 taille carré pour seulement N éléments, ou une efficacité de 1:(N-1)/4, par rapport à une forme EN I qui serait 1:1. Il se peut aussi que le inhérents invariant imposées par l'architecture serait effectivement moins efficace que l'algorithme naïf.
ma suspicion est que la préoccupation ci-dessus peut être allégée en simulant l'épuisement cartésien en convertissant l'ensemble des Noeuds en un graphe bi-directionnel qui peut être traversé, provoquant la noeuds à frapper dans le même ordre que mon algorithme de hachage beaucoup plus naïf, ignorant les espaces vides. Cela ramènera l'algorithme à O(n) comme le graphique doit pouvoir être construit en O(n) fuseau. Parce que je n'ai pas fait ça, Je ne peux pas en être sûr, c'est pourquoi je dis que ce n'est qu'un soupçon, mais il devrait y avoir un moyen de le faire.
Voici les explications de ma DFS (depth first search):
commencez par la cellule la plus haute (la plus à gauche en tant que briseur de tares). Marquer comme visité. Chaque fois que vous visitez une cellule, vérifiez les quatre directions pour les voisins non invités. Vérifiez toujours les quatre directions dans cet ordre: haut, gauche, bas, droite.
Exemple
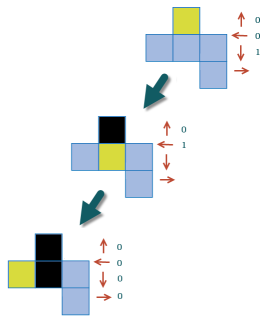
dans cet exemple, up et left échouent, mais down réussit. Jusqu'à présent notre production est 001, et nous recherchons récursivement le cellule "basse".
nous marquons notre nouvelle cellule actuelle telle que visitée (et nous finirons la recherche de la cellule d'origine lorsque nous aurons fini la recherche de cette cellule). Ici, up=0, left = 1.
nous recherchons la cellule la plus à gauche et il n'y a pas de voisins non avertis (up=0, left=0, down=0, right=0). Notre production totale à ce jour est de 001010000.
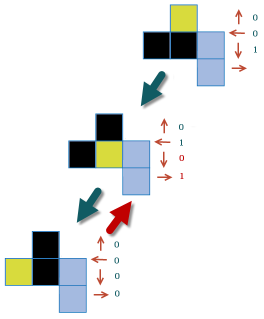
Nous continuons notre recherche de la deuxième cellule. down=0, droite=1. Nous cherchons la cellule à la droit.
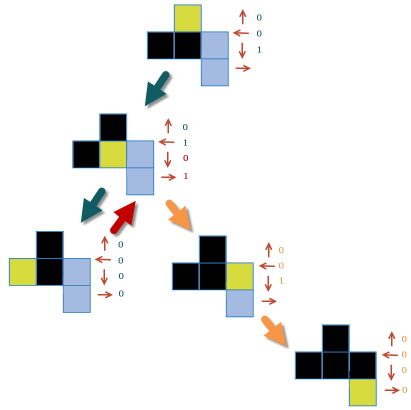
=0, left=0,=1. Fouillez la cellule du bas: tous les 0. La production totale à ce jour est de 001010000010010000. Puis, nous revenons de la cellule du bas...
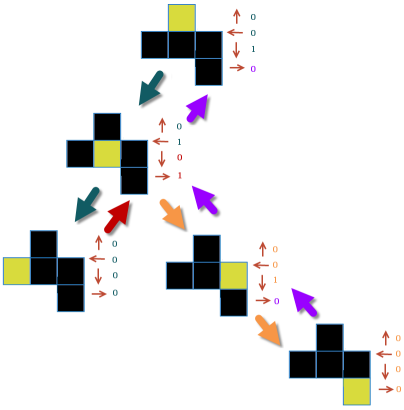
droite=0, retour. retourner. (Maintenant, nous sommes à la cellule de départ.) droite=0. Fait!
ainsi, la sortie totale est de 20 (N*4) bits: 00101000001001000000.
amélioration de L'encodage
Mais, nous pouvons enregistrer quelques morceaux.
la dernière cellule visitée encodera toujours 0000 pour ses quatre directions. Ainsi, ne pas encoder la dernière cellule visitée pour sauver 4 bits.
une autre amélioration: si vous avez atteint une cellule en déplaçant à gauche, ne Vérifiez pas que les cellules à droite. Donc, nous n'avons besoin que de 3 bits par cellule, sauf 4 bits pour la première cellule, et 0 pour la dernière cellule.
la première cellule n'aura jamais de voisin haut, ou gauche, donc omettez ces bits. Donc la première cellule prend 2 cents.
Donc, avec ces améliorations, nous n'utilisons que N*3-4 bits (par exemple 5 cellules -> 11 bits; 9 cellules -> 23 bits).
Si vous voulez vraiment, vous pouvez compacter un peu plus en notant que exactement N-1 bits sera "1".
Avertissement
Oui, vous aurez besoin d'encoder les 8 rotations/flips du polyomino et de choisir le moins pour obtenir un encodage canonique.
je pense que ce sera encore plus rapide que l'approche de contour. De plus, les trous dans le polyomino ne devraient pas être problème.
j'ai travaillé sur le même problème récemment. J'ai résolu le problème assez simplement par (1) générer un ID unique pour un polyomino, de sorte que chaque poly identique aurait le même UID. Par exemple, trouvez la boîte de délimitation, normalisez le coin de la boîte de délimitation et recueillez l'ensemble des cellules non vides. (2) générer toutes les permutations possibles en tournant (et en retournant, s'il y a lieu) un polyomino, et chercher les doublons.
L'avantage de cette approche brute, d'autres que c'est la simplicité, c'est qu'il fonctionne encore si l' les polys sont distinguables d'une autre manière, par exemple si certains d'entre eux sont colorés ou numérotés.
Vous pouvez mettre en place quelque chose comme trie pour identifier de façon unique (et pas seulement hachage) votre polyomino. Prenez votre polyomino normalisé et de mettre en place un arbre de recherche binaire, où les branches de racine sur si (0,0) est a un pixel fixé, les branches de niveau suivant sur si (0,1) a un pixel fixé, et ainsi de suite. Lorsque vous cherchez un polyomino, il suffit de le normaliser et puis marcher l'arbre. Si tu le trouves dans le trie, alors c'est fini. Si ce n'est pas le cas, assignez à ce polyomino un id unique (incrémenter simplement un counter), générer les 8 rotations et flips possibles, puis ajouter ces 8 à la trie.
sur une erreur de trie, vous devrez générer toutes les rotations et réflexions. Mais sur un coup de trie il devrait coûter moins (O (K^2) pour K-polyominos).
pour rendre les recherches encore plus efficaces, vous pouvez utiliser quelques bits à la fois et utiliser un arbre plus large au lieu d'un arbre binaire.
une fonction de hachage valide, si vous avez vraiment peur des collisions de hachage, est de faire une fonction de hachage x + ordre * y pour les coordonnées et ensuite boucler toutes les coordonnées d'une pièce, en ajoutant (ordre ^ i) * hachage(coord[i]) au hachage de pièce. De cette façon, vous pouvez garantir que vous n'aurez pas de collisions de hachage.