Algorithme pour générer un polygone 2D aléatoire
Je ne sais pas comment aborder ce problème. Je ne suis pas sûr de la complexité de la tâche. Mon objectif est d'avoir un algorithme qui génère un polygone. Ma seule exigence est que le polygone n'est pas complexe (c.-à-d. les côtés ne se croisent pas). J'utilise Matlab pour faire les maths, mais tout ce qui est abstrait est le bienvenu.
une aide/direction?
EDIT:
je pensais plutôt au code qui pourrait générer n'importe quel polygone, même des choses comme ceci:

5 réponses
il y a une bonne façon de faire ce que vous voulez en profitant des classes MATLAB DelaunayTri et TriRep et les diverses méthodes qu'ils emploient pour manipuler les mailles triangulaires. Le code ci-dessous suit ces étapes pour créer un simple polygone :
-
générez un nombre de points aléatoires égal au nombre désiré de côtés plus un facteur de caramel. Le facteur fudge assure que, quel que soit le résultat de la triangulation, nous devrions avoir assez de facettes pour être en mesure de couper la maille triangulaire vers le bas à un polygone avec le nombre désiré de côtés.
-
créer une triangulation Delaunay des points, résultant en un polygone convexe qui est construit à partir d'une série de facettes triangulaires.
-
Si la limite de la la triangulation a plus d'arêtes que désiré, choisir une facette triangulaire aléatoire sur le bord qui a un sommet unique (i.e. le triangle ne partage qu'un bord avec le reste de la triangulation). L'enlèvement de cette facette triangulaire réduira le nombre de bordures.
-
si la limite de la triangulation a moins d'arêtes que désirée, ou l'étape précédente n'a pas été en mesure de trouver un triangle à enlever, choisir une facette triangulaire au hasard sur le bord qui a un seul de ses bords sur la limite de triangulation. L'enlèvement de cette facette triangulaire augmentera le nombre de bordures.
-
si aucune facette triangulaire ne peut être trouvée correspondant aux critères ci-dessus, postez un avertissement qu'un polygone avec le nombre voulu de côtés n'a pas pu être trouvé et retournez les coordonnées x et y de la limite actuelle de la triangulation. Sinon, continuer à enlever les facettes triangulaires jusqu'à ce que le nombre désiré de bords est atteint, puis renvoie les coordonnées x et y de la limite de triangulation.
Voici la fonction résultante:
function [x, y, dt] = simple_polygon(numSides)
if numSides < 3
x = [];
y = [];
dt = DelaunayTri();
return
end
oldState = warning('off', 'MATLAB:TriRep:PtsNotInTriWarnId');
fudge = ceil(numSides/10);
x = rand(numSides+fudge, 1);
y = rand(numSides+fudge, 1);
dt = DelaunayTri(x, y);
boundaryEdges = freeBoundary(dt);
numEdges = size(boundaryEdges, 1);
while numEdges ~= numSides
if numEdges > numSides
triIndex = vertexAttachments(dt, boundaryEdges(:,1));
triIndex = triIndex(randperm(numel(triIndex)));
keep = (cellfun('size', triIndex, 2) ~= 1);
end
if (numEdges < numSides) || all(keep)
triIndex = edgeAttachments(dt, boundaryEdges);
triIndex = triIndex(randperm(numel(triIndex)));
triPoints = dt([triIndex{:}], :);
keep = all(ismember(triPoints, boundaryEdges(:,1)), 2);
end
if all(keep)
warning('Couldn''t achieve desired number of sides!');
break
end
triPoints = dt.Triangulation;
triPoints(triIndex{find(~keep, 1)}, :) = [];
dt = TriRep(triPoints, x, y);
boundaryEdges = freeBoundary(dt);
numEdges = size(boundaryEdges, 1);
end
boundaryEdges = [boundaryEdges(:,1); boundaryEdges(1,1)];
x = dt.X(boundaryEdges, 1);
y = dt.X(boundaryEdges, 2);
warning(oldState);
end
Et voici quelques exemples de résultats:
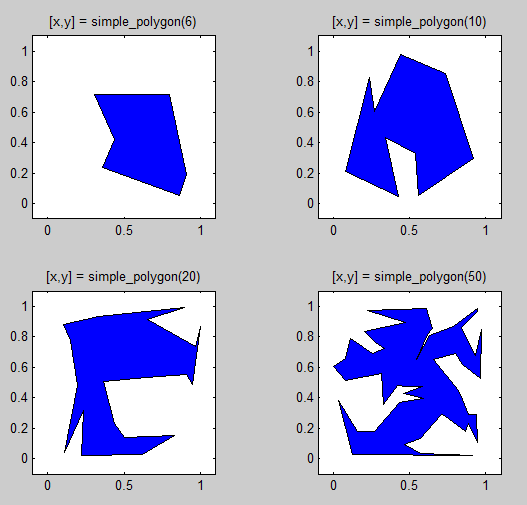
les polygones générés peuvent être convexes ou concaves , mais pour un plus grand nombre de côtés désirés ils seront presque certainement concaves. Les polygones sont aussi généré à partir de points générés au hasard à l'intérieur d'un carré unitaire, de sorte que les polygones ayant un plus grand nombre de côtés auront généralement l'air d'avoir une limite "carrée" (comme l'exemple en bas à droite ci-dessus avec le polygone à 50 côtés). Pour modifier cette forme limite générale, vous pouvez changer la façon dont les points initiaux x et y sont choisis au hasard (c.-à-d. à partir d'une distribution gaussienne, etc.).
j'ai pris l'idée de @MitchWheat et @templatetypedef de points d'échantillonnage sur un cercle et je l'ai prise un peu plus loin.
dans mon application, je dois être capable de contrôler comment les polygones sont bizarres, c'est-à-dire de commencer avec des polygones réguliers et que j'augmente les paramètres ils deviennent de plus en plus chaotiques. L'idée de base est comme indiqué par @templatetypedef; marchez autour du cercle en faisant un pas angulaire aléatoire à chaque fois, et à chaque pas mettez un point à un rayon aléatoire. Dans les équations je suis générer les pas angulaires comme
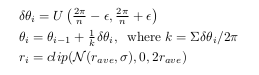
où thetaii et r_i donnent l'angle et le rayon de chaque point par rapport au centre, U(min, max) tire un nombre aléatoire d'une distribution uniforme, et N(mu, sigma) tire un nombre aléatoire d'une distribution gaussienne, et clip(X, min, max) indique une valeur dans une plage. Cela nous donne deux paramètres vraiment agréable pour contrôler comment wild les polygones sont-epsilon que je vais appeler irrégularité contrôle si les points sont uniformément l'espace angulaire autour du cercle, et sigma que je vais appeler spikeyness qui contrôle combien les points peuvent varier du cercle de rayon r_ave. Si vous définissez ces deux à 0, puis vous obtenez parfaitement les polygones réguliers, si vous manivelle jusqu'alors les polygones obtenir plus fou.
j'ai préparé ça rapidement en python et j'ai des trucs comme ça:
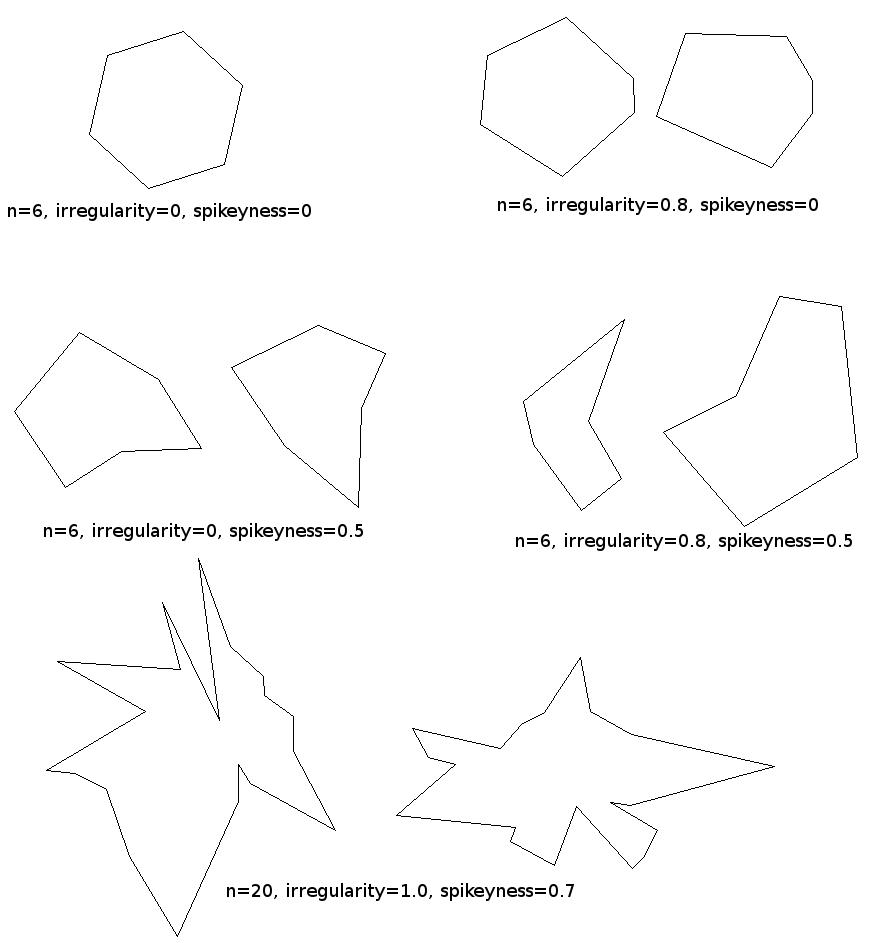
voici le code python complet:
import math, random
def generatePolygon( ctrX, ctrY, aveRadius, irregularity, spikeyness, numVerts ) :
'''Start with the centre of the polygon at ctrX, ctrY,
then creates the polygon by sampling points on a circle around the centre.
Randon noise is added by varying the angular spacing between sequential points,
and by varying the radial distance of each point from the centre.
Params:
ctrX, ctrY - coordinates of the "centre" of the polygon
aveRadius - in px, the average radius of this polygon, this roughly controls how large the polygon is, really only useful for order of magnitude.
irregularity - [0,1] indicating how much variance there is in the angular spacing of vertices. [0,1] will map to [0, 2pi/numberOfVerts]
spikeyness - [0,1] indicating how much variance there is in each vertex from the circle of radius aveRadius. [0,1] will map to [0, aveRadius]
numVerts - self-explanatory
Returns a list of vertices, in CCW order.
'''
irregularity = clip( irregularity, 0,1 ) * 2*math.pi / numVerts
spikeyness = clip( spikeyness, 0,1 ) * aveRadius
# generate n angle steps
angleSteps = []
lower = (2*math.pi / numVerts) - irregularity
upper = (2*math.pi / numVerts) + irregularity
sum = 0
for i in range(numVerts) :
tmp = random.uniform(lower, upper)
angleSteps.append( tmp )
sum = sum + tmp
# normalize the steps so that point 0 and point n+1 are the same
k = sum / (2*math.pi)
for i in range(numVerts) :
angleSteps[i] = angleSteps[i] / k
# now generate the points
points = []
angle = random.uniform(0, 2*math.pi)
for i in range(numVerts) :
r_i = clip( random.gauss(aveRadius, spikeyness), 0, 2*aveRadius )
x = ctrX + r_i*math.cos(angle)
y = ctrY + r_i*math.sin(angle)
points.append( (int(x),int(y)) )
angle = angle + angleSteps[i]
return points
def clip(x, min, max) :
if( min > max ) : return x
elif( x < min ) : return min
elif( x > max ) : return max
else : return x
@MateuszKonieczny voici du code pour créer une image d'un polygone à partir d'une liste de Sommets.
verts = generatePolygon( ctrX=250, ctrY=250, aveRadius=100, irregularity=0.35, spikeyness=0.2, numVerts=16 )
black = (0,0,0)
white=(255,255,255)
im = Image.new('RGB', (500, 500), white)
imPxAccess = im.load()
draw = ImageDraw.Draw(im)
tupVerts = map(tuple,verts)
# either use .polygon(), if you want to fill the area with a solid colour
draw.polygon( tupVerts, outline=black,fill=white )
# or .line() if you want to control the line thickness, or use both methods together!
draw.line( tupVerts+[tupVerts[0]], width=2, fill=black )
im.show()
# now you can save the image (im), or do whatever else you want with it.
pour un polygone 2D convexe (complètement sorti de ma tête):
-
la génération aléatoire de rayon, R
-
générer N points aléatoires sur la circonférence D'un cercle de rayon R
-
faites le tour du cercle et tracez des lignes droites entre les points adjacents du cercle.
comme @templatetypedef et @MitchWheat l'ont dit, il est facile de le faire en générant N angles aléatoires et rayons. Il est important de trier les angles, sinon il ne sera pas un simple polygone. Notez que j'utilise une astuce soignée pour dessiner des courbes fermées - Je l'ai décrit dans ici . D'ailleurs, les polygones pourraient être concave .
Notez que tous ces polygones sont en forme d'étoile. La génération d'un plus générale polygone n'est pas un problème simple. Juste pour vous donner un avant-goût du problème - découvrez http://www.cosy.sbg.ac.at/~held/projects/rpg/rpg.html et http://compgeom.cs.uiuc.edu/~jeffe/open/randompoly.html .
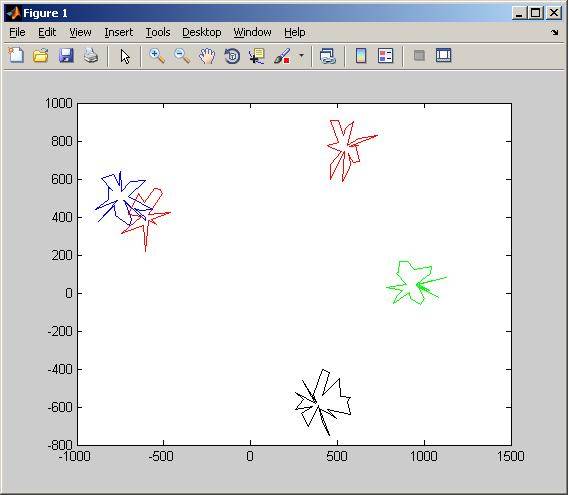
function CreateRandomPoly()
figure();
colors = {'r','g','b','k'};
for i=1:5
[x,y]=CreatePoly();
c = colors{ mod(i-1,numel(colors))+1};
plotc(x,y,c);
hold on;
end
end
function [x,y]=CreatePoly()
numOfPoints = randi(30);
theta = randi(360,[1 numOfPoints]);
theta = theta * pi / 180;
theta = sort(theta);
rho = randi(200,size(theta));
[x,y] = pol2cart(theta,rho);
xCenter = randi([-1000 1000]);
yCenter = randi([-1000 1000]);
x = x + xCenter;
y = y + yCenter;
end
function plotc(x,y,varargin)
x = [x(:) ; x(1)];
y = [y(:) ; y(1)];
plot(x,y,varargin{:})
end
voici un port de travail pour Matlab of Mike Ounsworth solution. Je n'ai pas optimisé pour matlab. Je peut mettre à jour la solution plus tard.
function [points] = generatePolygon(ctrX, ctrY, aveRadius, irregularity, spikeyness, numVerts)
%{
Start with the centre of the polygon at ctrX, ctrY,
then creates the polygon by sampling points on a circle around the centre.
Randon noise is added by varying the angular spacing between sequential points,
and by varying the radial distance of each point from the centre.
Params:
ctrX, ctrY - coordinates of the "centre" of the polygon
aveRadius - in px, the average radius of this polygon, this roughly controls how large the polygon is, really only useful for order of magnitude.
irregularity - [0,1] indicating how much variance there is in the angular spacing of vertices. [0,1] will map to [0, 2pi/numberOfVerts]
spikeyness - [0,1] indicating how much variance there is in each vertex from the circle of radius aveRadius. [0,1] will map to [0, aveRadius]
numVerts - self-explanatory
Returns a list of vertices, in CCW order.
Website: https://stackoverflow.com/questions/8997099/algorithm-to-generate-random-2d-polygon
%}
irregularity = clip( irregularity, 0,1 ) * 2*pi/ numVerts;
spikeyness = clip( spikeyness, 0,1 ) * aveRadius;
% generate n angle steps
angleSteps = [];
lower = (2*pi / numVerts) - irregularity;
upper = (2*pi / numVerts) + irregularity;
sum = 0;
for i =1:numVerts
tmp = unifrnd(lower, upper);
angleSteps(i) = tmp;
sum = sum + tmp;
end
% normalize the steps so that point 0 and point n+1 are the same
k = sum / (2*pi);
for i =1:numVerts
angleSteps(i) = angleSteps(i) / k;
end
% now generate the points
points = [];
angle = unifrnd(0, 2*pi);
for i =1:numVerts
r_i = clip( normrnd(aveRadius, spikeyness), 0, 2*aveRadius);
x = ctrX + r_i* cos(angle);
y = ctrY + r_i* sin(angle);
points(i,:)= [(x),(y)];
angle = angle + angleSteps(i);
end
end
function value = clip(x, min, max)
if( min > max ); value = x; return; end
if( x < min ) ; value = min; return; end
if( x > max ) ; value = max; return; end
value = x;
end