Algorithme pour trouver une solution au puzzle
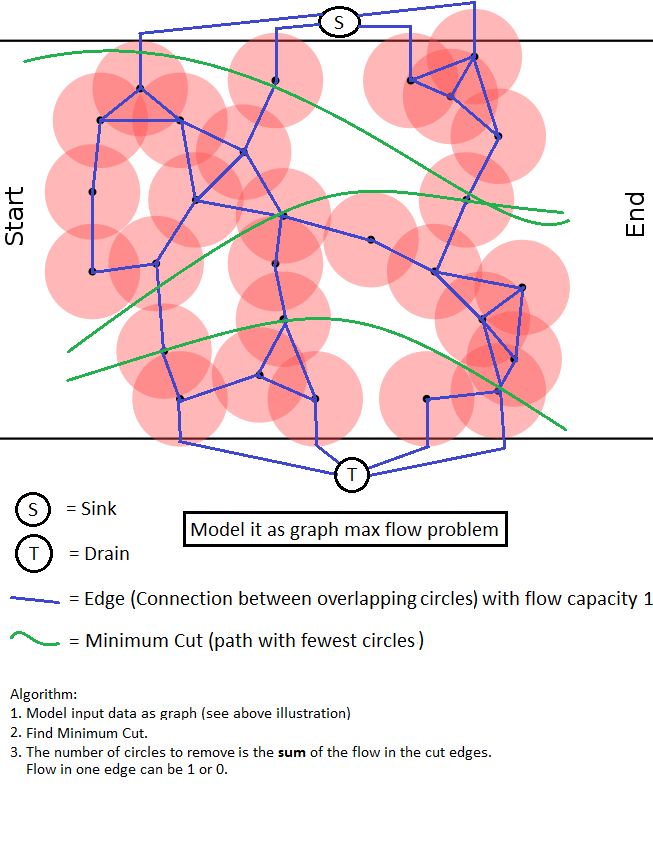
J'essaie de faire un jeu où un joueur doit trouver son chemin du début à la fin sur le plateau de jeu. ![Plateau de jeu][1]
Comme vous le voyez, ce plateau de jeu contient un tas d'obstacles circulaires rouges. Pour gagner le jeu, le joueur doit supprimer un minimum d'obstacles. Donc, ma question Est, Comment puis-je trouver par programme le montant minimum d'obstacles à supprimer, pour libérer un chemin? Un chemin libre serait considéré comme l'espace entre, les cercles ne se chevauchent pas et ne se touchent pas.
Donc ce dont j'ai vraiment besoin, c'est de la quantité minimale de cercles à supprimer, Je n'ai pas besoin du chemin réel. Est-il un moyen facile de faire cela?
Et pour compléter la compréhension de ce plateau de Jeu, Les cercles ont chacun le même rayon, et il est limité par les lignes noires.
Il N'est pas non plus nécessaire de se déplacer en ligne droite.
5 réponses
C'est un problème de théorie des graphes maximum flow.
Supposons que chaque cercle est un nœud dans le graphe. En outre introduire 2 nœuds Spéciaux: TOP et BOTTOM. Connectez les cercles avec ces nœuds s'ils se croisent avec le côté supérieur/inférieur. Connectez les nœuds correspondant aux cercles les uns avec les autres si les cercles se croisent.
Maintenant, vous devez trouver une coupe minimale dans ce graphique, ayant TOP comme source et BOTTOM comme évier ou vice versa. Vous pouvez utiliser Max-flow_min-cut_theorem pour le résoudre. Ce qu'il indique, c'est que Minimum-cut problem est équivalent au problème Max-flow. Vous pouvez trouver des détails sur la façon de résoudre Max-Flow problem sur TopCoder .
Comme nous ne pouvons passer par chaque nœud qu'une seule fois, nous devrions convertir les nœuds en un bord dirigé de capacité un avec in-node et out-node pour chaque cercle. L'algorithme Max-flow résoudra le problème sur le graphique résultant et tiendra compte du fait que nous supprimons des cercles plutôt que des connexions entre les cercles. C'est toujours une meilleure décision pour ce problème de supprimer un nœud dans un graphique plutôt qu'un bord, car nous pouvons toujours supprimer n'importe quel bord en supprimant un nœud. La suppression d'un nœud peut en outre entraîner la suppression de plus d'un bord.
En passant, un problème similaire peut être trouvé sur UVA juge en ligne . C'est une bonne idée d'essayer de résoudre cette tâche sur le juge, alors vous serez sûr que votre solution est correcte.
En essayant de visualiser ce que Leonid a écrit, j'ai fait le diagramme suivant.
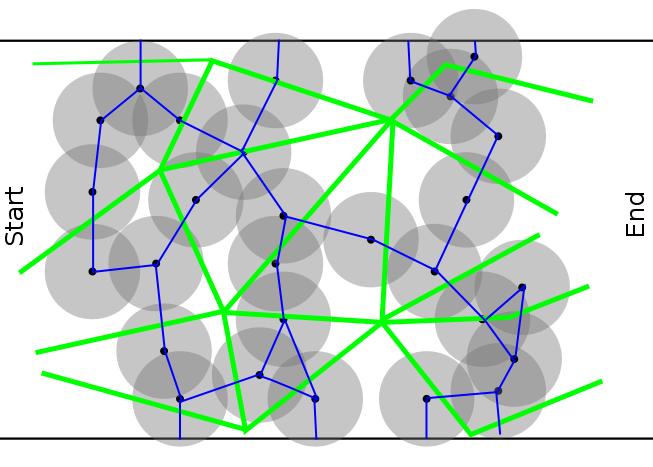
Pour une traduction de graphique, quelque chose comme ça pourrait fonctionner.
Faites un mur (les lignes bleues) entre deux cercles s'ils se chevauchent. N'oubliez pas d'ajouter dans la bordure supérieure et inférieure ainsi. Cela crée un couple de régions. Ce seront tous les nœuds du graphique.
Ensuite, nous devons trouver les bords, le coût d'aller d'un nœud à l'autre. Prenez deux régions voisines (partageant un mur.) Ensuite, par la force brute, ou Quelle méthode intelligente vous venez avec, déterminer le coût de le déplacement de cette région à l'autre. Si vous supprimez un cercle, cela signifie que vous supprimez tous les murs qui vont à ce cercle. Si cela rend les deux régions en une seule région, le coût de l'arête est de 1. Si vous devez supprimer deux cercles (tous les murs qu'ils ont) pour combiner les deux régions, le coût est de 2. Etc.
Certains bords (verts) sont dessinés. Nous devons aller de la région de départ à la région de fin. Vous avez maintenant un graphique pondéré tous les jours.
Je pense que cela peut être beaucoup amélioré, mais Je laisse cela comme un exercice =)
Dans ce cas, le minimum est de 3.
Attention, l'image est dessinée à la main, j'ai oublié quelques murs, bords et régions. Pour fins d'illustration seulement.
Très bien, j'ai donc décidé de faire une visualisation de cela dans pygame.
Il s'est avéré être beaucoup plus difficile que prévu.
L'idée que dans d'autres suggestions est d'utiliser Débit Maxi. Le goulot d'étranglement dans l'écoulement de la source au puits est l'endroit où l'écoulement est le plus dense. Si nous coupons le graphique en deux à ce col de bouteille dense, (c'est-à-dire à la min-cut) alors nous avons le nombre minimum de cercles. Il arrive le maxflow = min-cut.
Voici les étapes que j'ai prises:
-
Créer un monde pygame où je peux générer aléatoirement des cercles
Faire fonctionner pour travailler sur toutes les collisions entre les cercles:
Cela impliquait de trier les cercles par coordonnée X. Maintenant, pour trouver toutes les collisions de Circle [0], Je continue à me déplacer le long du tableau en testant les collisions jusqu'à ce que je trouve un cercle dont la valeur x est supérieure à 2 * rayon supérieur à la valeur X de circle[0], alors je peux faire apparaître circle [0] et répéter le processus..
- créez des nœuds source et évier , déterminez les cercles auxquels ils doivent se connecter.
Les étapes 4-5 sont effectuées dans la fonction "findflow() "
Créez un graphique networkX non orienté de base représentant des cercles avec des nœuds. Connexion des nœuds uniquement si leurs cercles correspondants entrent en collision.
-
Et c'est là que ça commence à devenir dur.. Je crée un nouveau graphe dirigé à partir de mon graphe non orienté . Parce J'avais besoin de travailler sur le flux à travers les cercles (c'est-à-dire les nœuds) pas les bords, j'ai besoin de diviser chaque nœud en deux nœuds avec un bord entre.
Disons que j'ai le nœud X connecté au nœud Y (YX) (dans le graphique d'origine).
Je change X en Xa et Xb pour que Xa se connecte à Xb (Xa- > Xb) Y change également en (Ya - >Yb).
J'ai aussi besoin d'ajouter (Yb- > Xa) et (Xb->Ya) pour représenter la connexion d'origine entre X et Y.
Toutes les arêtes du graphe non orienté sont données capacity=1 (par exemple, vous ne pouvez traverser un cercle qu'une seule fois)
- j'applique maintenant networkx.ford_fulkerson() algorithme sur mon nouveau graphe orienté. Cela me trouve le flowValue et le flowGraph.
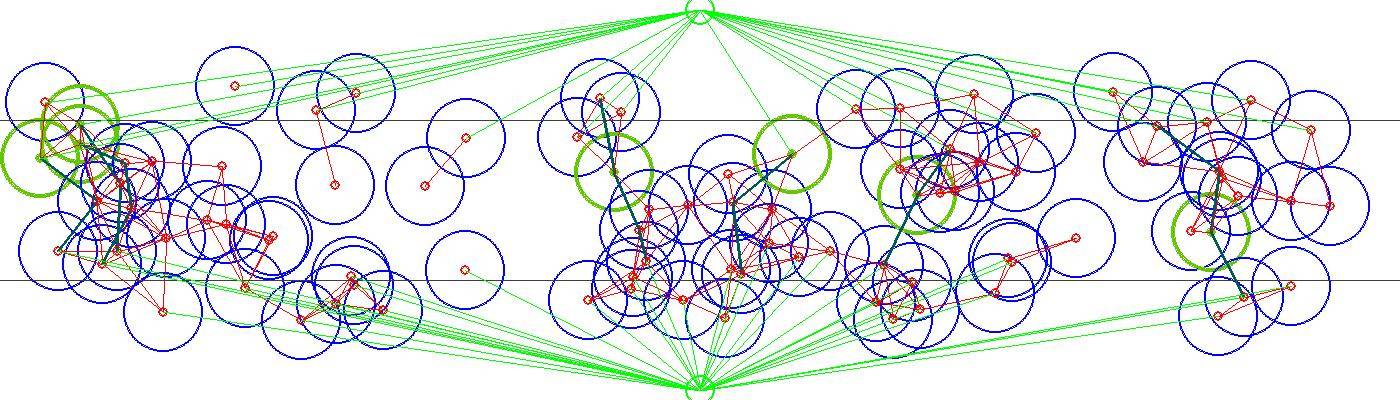
La valeur de flux est un entier. C'est la coupe min (ou débit max de la source à l'évier). C'est la réponse que nous cherchions. Il représente le nombre minimum de cercles que nous devons supprimer.
Affectation De Bonus:
Je pensais.. pourquoi arrêtez-vous ici, avoir le nombre de cercles à supprimer est agréable, mais je veux connaître les cercles exacts que je dois supprimer. Pour ce faire, j'ai besoin de savoir où la min-cut se produit réellement sur le flowGraph. J'ai réussi à comprendre comment faire cela, mais mon implémentation a un bug quelque part, donc il prend parfois la Coupe légèrement mal et obtient ainsi les mauvais cercles.
Pour trouver le min-cut, nous utiliserons le flowGraph produit à l'étape 6. L'idée est que le goulot d'étranglement de ce graphique sera la min-cut. si nous essayons de couler de la source à l'évier, nous serons coincés au goulot de la bouteille car tous les bords autour du goulot d'étranglement seront à leur capacité maximale. Nous utilisons donc simplement DFS ( Depth first search ) pour descendre aussi loin que possible. Le DFS est uniquement autorisé à se déplacer le long des bords qui ne sont pas à la capacité maximale dans le graphique de flux. (par exemple, leur flux est 0 et non 1). En utilisant DFS de la source, j'ai gardé note de tous les nœuds que je pouvais voir les stocker dans self.voir. Maintenant, après DFS, pour tous les nœuds vus, je vérifiez si le nœud a un bord de capacité maximale à un nœud qui n'a pas été vu dans DFS. Tous ces nœuds sont sur le min-cut.
Voici une image de l'une des simulations que j'ai effectuées:
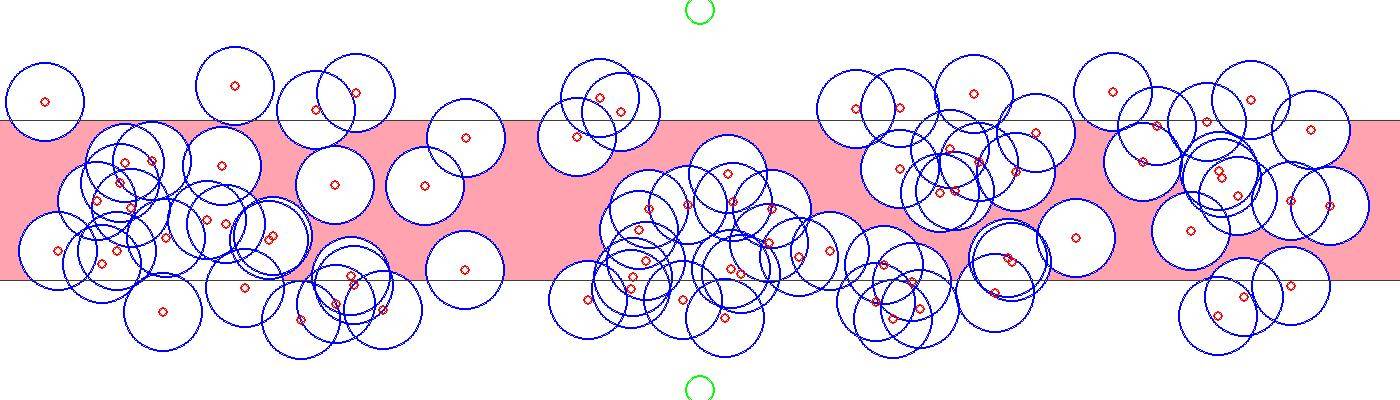
Et avec les cercles supprimés, Je l'ai rempli de peinture (vous devrez peut-être zoomer un peu pour voir qu'il y a effectivement un écart entre les cercles):
Apprentissages:
La vitesse est ok même en python, fonctionne pour 1000 cercles ok.
C'était plus dur que je ne le pensais, et je encore un bug en essayant d'utiliser le DFS pour trouver les cercles d'origine. (Si quelqu'un peut aider à trouver le bug, ce serait génial).
Le code était élégant au début, bien que j'ai continué à ajouter des hacks pour changer la visualisation, etc.
Code de travail (à l'exception d'un léger bug occasionnel dans DFS):
__author__ = 'Robert'
import pygame
import networkx
class CirclesThing():
def __init__(self,width,height,number_of_circles):
self.removecircles = False #display removable circles as green.
self.width = width
self.height = height
self.number_of_circles = number_of_circles
self.radius = 40
from random import randint
self.circles = sorted(set((randint(self.radius,width-self.radius),randint(2*self.radius,height-2*self.radius)) for i in range(self.number_of_circles)))
self.sink = (self.width/2, self.height-10)
self.source = (self.width/2, 10)
self.flowValue,self.flowGraph = self.find_flow()
self.seen = set()
self.seen.add(self.source)
self.dfs(self.flowGraph,self.source)
self.removable_circles = set()
for node1 in self.flowGraph:
if node1 not in self.seen or node1==self.source:
continue
for node2 in self.flowGraph[node1]:
if self.flowGraph[node1][node2]==1:
if node2 not in self.seen:
self.removable_circles.add(node1[0])
def find_flow(self):
"finds the max flow from source to sink and returns the amount, along with the flow graph"
G = networkx.Graph()
for node1,node2 in self.get_connections_to_source_sink()+self.intersect_circles():
G.add_edge(node1,node2,capacity=1)
G2 = networkx.DiGraph()
for node in G:
if node not in (self.source,self.sink):
G2.add_edge((node,'a'),(node,'b'),capacity=1) #each node is split into two new nodes. We add the edge between the two new nodes flowing from a to b.
for edge in G.edges_iter():
if self.source in edge or self.sink in edge:
continue #add these edges later
node1,node2 = edge
G2.add_edge((node1,'b'),(node2,'a'),capacity=1) #if we flow through a circle (from node1a to node1b) we need to be able to flow from node1b to all node1's children
G2.add_edge((node2,'b'),(node1,'a'),capactiy=1) #similarly for node2..
for node in G[self.source]:
G2.add_edge(self.source,(node,'a'))
for node in G[self.sink]:
G2.add_edge((node,'b'),self.sink)
flowValue, flowGraph = networkx.ford_fulkerson(G2,self.source,self.sink)
return flowValue, flowGraph
def dfs(self,g,v):
"depth first search from source of flowGraph. Don't explore any nodes that are at maximum capacity. (this means we can't explore past the min cut!)"
for node in g[v]:
if node not in self.seen:
self.seen.add(node)
if g[v][node]!=1 or v==self.source:
self.dfs(g,node)
def display(self):
self.draw_circles()
self.draw_circles(circle_radius=5, circle_colour=(255,0,0))
if not self.removecircles:
lines = self.intersect_circles()
self.draw_lines(lines)
self.draw_source_sink()
def draw_circles(self,circle_radius=None,circle_colour=(0,0,255),circles=None):
if circle_radius is None:
circle_radius = self.radius
if circles is None:
circles = self.circles
circle_thickness = 2
for pos in circles:
cc = circle_colour if pos not in self.removable_circles else (100,200,0) #change colour of removable circles
ct = circle_thickness if pos not in self.removable_circles else 4 #thicken removable circles
if pos not in self.removable_circles or not self.removecircles:
pygame.draw.circle(screen, cc, pos, circle_radius, ct)
def intersect_circles(self):
colliding_circles = []
for i in range(len(self.circles)-1):
for j in range(i+1,len(self.circles)):
x1,y1 = self.circles[i]
x2,y2 = self.circles[j]
if x2-x1>2*self.radius+5: #add 5 to make a more obvious gap visually
break #can't collide anymore.
if (x2-x1)**2 + (y2-y1)**2 <= (2*self.radius)**2+5:
colliding_circles.append(((x1,y1),(x2,y2)))
return colliding_circles
def draw_lines(self,lines,line_colour=(255, 0, 0)):
for point_pair in lines:
point1,point2 = point_pair
try:
tot = self.flowGraph[(point1,'b')][(point2,'a')] + self.flowGraph[(point2,'b')][(point1,'a')] #hack, does anything flow between the two circles?
except KeyError:
tot = 0
thickness = 1 if tot==0 else 3
lc = line_colour if tot==0 else (0,90,90)
pygame.draw.line(screen, lc, point1, point2, thickness)
def draw_source_sink(self):
self.draw_circles(circles=(self.sink,self.source),circle_radius=15,circle_colour=(0,255,0))
bottom_line = ((0,self.height-3*self.radius),(self.width,self.height-3*self.radius))
top_line = ((0,3*self.radius),(self.width,3*self.radius))
self.draw_lines([top_line, bottom_line],line_colour=(60,60,60))
if not self.removecircles:
self.draw_lines(self.get_connections_to_source_sink(),line_colour=(0,255,0))
def get_connections_to_source_sink(self):
connections = []
for x,y in self.circles:
if y<4*self.radius:
connections.append((self.source,(x,y)))
elif y>height-4*self.radius:
connections.append((self.sink,(x,y)))
return connections
def get_caption(self):
return "flow %s, circles removes %s" %(self.flowValue,len(self.removable_circles))
time_per_simulation = 5 #5 seconds
width, height = 1400, 600
background_colour = (255,255,255)
screen = pygame.display.set_mode((width, height))
screen.fill(background_colour)
from pygame.locals import USEREVENT
pygame.time.set_timer(USEREVENT+1,time_per_simulation*1000)
simulations = 0
simulations_max = 20
running = True
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
if event.type == USEREVENT+1:
if simulations % 2 ==0:
world = CirclesThing(width,height,120) #new world
else:
world.removecircles = True #current world without green circles
screen.fill(background_colour)
world.display()
pygame.display.set_caption(world.get_caption())
pygame.display.flip()
if simulations>=2*simulations_max:
running = False
simulations+=1
if False:
pygame.image.save(screen,'sim%s.bmp'%simulations)
Une option consiste à supprimer d'abord les cercles avec le plus grand nombre de chevauchements ou de touches. Après chacun de ceux que vous supprimez, vérifiez si c'est une solution, sinon continuez à supprimer.
var circle;
circle = findMostOverlapCircle();
while(circle != null) {
circle.remove();
circle = findMostOverlapCircle();
}