Algorithme pour déterminer efficacement l'élément [n][n] dans une matrice
il s'agit d'une question concernant un morceau de cours donc préféreriez-vous ne pas répondre entièrement à la question, mais plutôt donner des conseils pour améliorer la complexité du temps d'exécution de mon algorithme actuel.
j'ai reçu les informations suivantes:
Une fonction g(n) est donnée par g(n) = f(n,n) où f peut être définie de manière récursive par
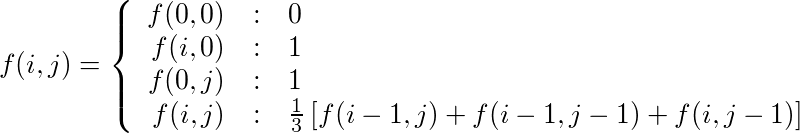
j'ai implémenté cet algorithme de façon récursive avec le suivant code:
public static double f(int i, int j)
{
if (i == 0 && j == 0) {
return 0;
}
if (i ==0 || j == 0) {
return 1;
}
return ((f(i-1, j)) + (f(i-1, j-1)) + (f(i, j-1)))/3;
}
cet algorithme donne les résultats que je recherche, mais il est extrêmement inefficace et je suis maintenant chargé d'améliorer la complexité du temps d'exécution.
j'ai écrit un algorithme pour créer une matrice n*n et il calcule ensuite chaque élément jusqu'à l'élément [n][n] dans lequel il renvoie alors l'élément [n][n], Par exemple f(1,1) renvoie 0,6 récurrent. L'élément [n][n] est 0,6 récurrent car il est le résultat (1+0+1)/3.
j'ai aussi créé une feuille de calcul du résultat de f(0,0) f(7,7) qui peut être vu ci-dessous:
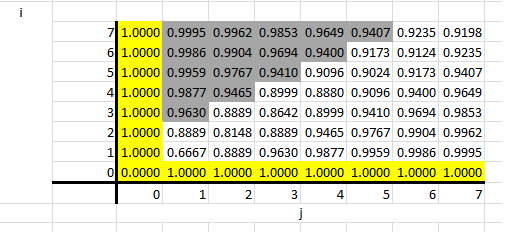
bien que ce soit beaucoup plus rapide que mon algorithme récursif, il a une énorme charge de création d'une matrice n*N.
toute suggestion sur la façon dont je peux améliorer cet algorithme sera grandement appréciée!
je peux maintenant Voir qu'il est possible de rendre l'algorithme O(n) complexe, mais est-il possible de travailler sur le résultat sans créer un [n][n] 2D tableau?
j'ai créé une solution en Java qui s'exécute en O(n) temps et O(n) espace et postera la solution après que j'ai remis dans mon travail de cours pour arrêter tout plagiat.
6 réponses
c'est une autre de ces questions où il est préférable de l'examiner, avant de plonger et d'écrire du code.
la première chose que je dirais que vous devriez faire est de regarder une grille des nombres, et de ne pas les représenter comme des décimales, mais des fractions à la place.
la première chose qui devrait être évidente est que le nombre total de 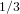 vous avez à faire est simplement une mesure de la distance de l'origine,
vous avez à faire est simplement une mesure de la distance de l'origine,  .
.
Si vous regardez une grille de cette façon, vous pouvez obtenir tous les dénominateurs:

notez que la première ligne et la première colonne ne sont pas toutes 1s-ils ont été choisis pour suivre le modèle, et la formule générale qui fonctionne pour tous les autres carrés.
Les numérateurs sont un peu plus délicat, mais reste faisable. Comme pour la plupart des problèmes comme celui-ci, la réponse est liée à des combinaisons, factoriels, et puis quelques choses plus compliquées. Les entrées typiques ici nombres de Catalan, les numéros de Stirling,triangle de Pascal, et vous aurez presque toujours voir fonctions Hypergéométriques utilisé.
sauf si vous faites un beaucoup en mathématiques, il est peu probable que vous connaissiez tout cela, et il y a un enfer de beaucoup de littérature. J'ai donc un moyen plus facile de découvrir les relations dont vous avez besoin, ce qui fonctionne presque toujours. Il va comme ceci:
- Écrire le naïf, l'algorithme inefficace pour obtenir la séquence que vous voulez.
- copiez une quantité raisonnablement grande des nombres dans google.
espérons qu'un résultat de online Encyclopedia of Integer Sequences s'affiche.
3.B. Si tel n'est pas le cas, examinez les différences dans votre séquence, ou toute autre séquence liée à vos données.
utilisez les informations que vous trouvez pour mettre en œuvre said séquence.
Donc, suivant cette logique, voici les numérateurs:
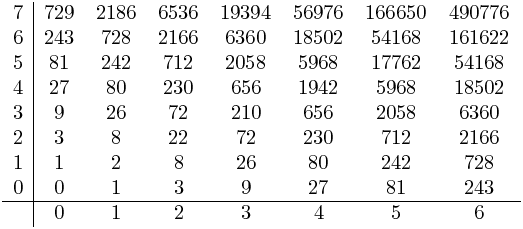
malheureusement, googler n'a rien donné. Cependant, il y a quelques choses que vous pouvez remarquer à leur sujet, la principale étant que la première rangée/colonne sont juste des puissances de 3, et que la deuxième rangée/colonne sont une de moins que les puissances de trois. Cette frontière de genre est exactement la même que le triangle de Pascal, et beaucoup de séquence.
Voici la matrice des différences entre les numérateurs et les dénominateurs:
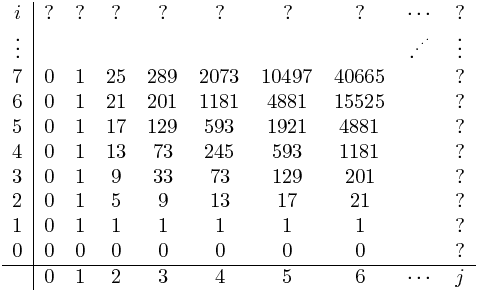
où nous avons décidé que l'élément f(0,0) suivrait le même modèle. Ces chiffres semblent déjà beaucoup plus simples. Notez cependant aussi-assez intéressant, que ces nombres suivent les mêmes règles que les nombres initiaux - sauf que le premier nombre est un (et ils sont compensés par une colonne et une rangée). T(i,j) = T(i-1,j) + T(i,j-1) + 3*T(i-1,j-1):
1
1 1
1 5 1
1 9 9 1
1 13 33 13 1
1 17 73 73 17 1
1 21 129 245 192 21 1
1 25 201 593 593 201 25 1
cela ressemble plus aux séquences que vous voyez beaucoup en combinatoire.
si vous googlez les nombres de cette matrice,vous obtenez un résultat.
Et puis si on coupe le lien pour les données brutes, vous obtenez la séquence A081578, qui est décrit comme un" tableau Pascal-(1,3,1)", qui a exactement du sens - si vous faites tourner la matrice, de sorte que le 0,0 élément est au top, et les éléments forment un triangle, puis vous prenez 1* l'élément de gauche,3* l'élément ci-dessus, et 1* le bon élément.
la question est maintenant d'implémenter les formules utilisées pour générer les nombres.
T (n,k)=somme{j=0..n,C(k,j-k)*C(N+k-j, k)*3^(j-k)}
c'est faux, et il faut un peu juste de la lecture le livre (lien sur la page) pour élaborer la formule correcte. Les sections que vous voulez sont la proposition 26, corollaire 28. La séquence est mentionnée au Tableau 2 après la proposition 13. Notez que r=4
la formule correcte est donnée dans la proposition 26, mais il y a aussi une faute de frappe :/. k=0 dans la somme doit être un j=0:
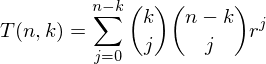
Où T est la matrice triangulaire contenant les coefficients.
L'OEIS page donne quelques implémentations pour calculer les nombres, mais aucun d'eux n'est en java, et aucun d'eux ne peut être facilement transcrit en java:
il y a un exemple de mathematica:
Table[ Hypergeometric2F1[-k, k-n, 1, 4], {n, 0, 10}, {k, 0, n}] // Flatten
qui, comme toujours, est ridiculement succincte. Et il y a aussi une version Haskell, qui est tout aussi courte:
a081578 n k = a081578_tabl !! n !! k
a081578_row n = a081578_tabl !! n
a081578_tabl = map fst $ iterate
(\(us, vs) -> (vs, zipWith (+) (map (* 3) ([0] ++ us ++ [0])) $
zipWith (+) ([0] ++ vs) (vs ++ [0]))) ([1], [1, 1])
je sais que vous faites cela en java, mais je n'ai pas pris la peine de transcrire ma réponse en java (désolé). Voici un python application:
from __future__ import division
import math
#
# Helper functions
#
def cache(function):
cachedResults = {}
def wrapper(*args):
if args in cachedResults:
return cachedResults[args]
else:
result = function(*args)
cachedResults[args] = result
return result
return wrapper
@cache
def fact(n):
return math.factorial(n)
@cache
def binomial(n,k):
if n < k: return 0
return fact(n) / ( fact(k) * fact(n-k) )
def numerator(i,j):
"""
Naive way to calculate numerator
"""
if i == j == 0:
return 0
elif i == 0 or j == 0:
return 3**(max(i,j)-1)
else:
return numerator(i-1,j) + numerator(i,j-1) + 3*numerator(i-1,j-1)
def denominator(i,j):
return 3**(i+j-1)
def A081578(n,k):
"""
http://oeis.org/A081578
"""
total = 0
for j in range(n-k+1):
total += binomial(k, j) * binomial(n-k, j) * 4**(j)
return int(total)
def diff(i,j):
"""
Difference between the numerator, and the denominator.
Answer will then be 1-diff/denom.
"""
if i == j == 0:
return 1/3
elif i==0 or j==0:
return 0
else:
return A081578(j+i-2,i-1)
def answer(i,j):
return 1 - diff(i,j) / denominator(i,j)
# And a little bit at the end to demonstrate it works.
N, M = 10,10
for i in range(N):
row = "%10.5f"*M % tuple([numerator(i,j)/denominator(i,j) for j in range(M)])
print row
print ""
for i in range(N):
row = "%10.5f"*M % tuple([answer(i,j) for j in range(M)])
print row
Donc, pour une fermeture de la forme:
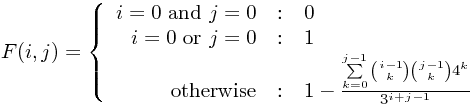
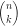 ne sont que des coefficients binomiaux.
ne sont que des coefficients binomiaux.
Voici le résultat:
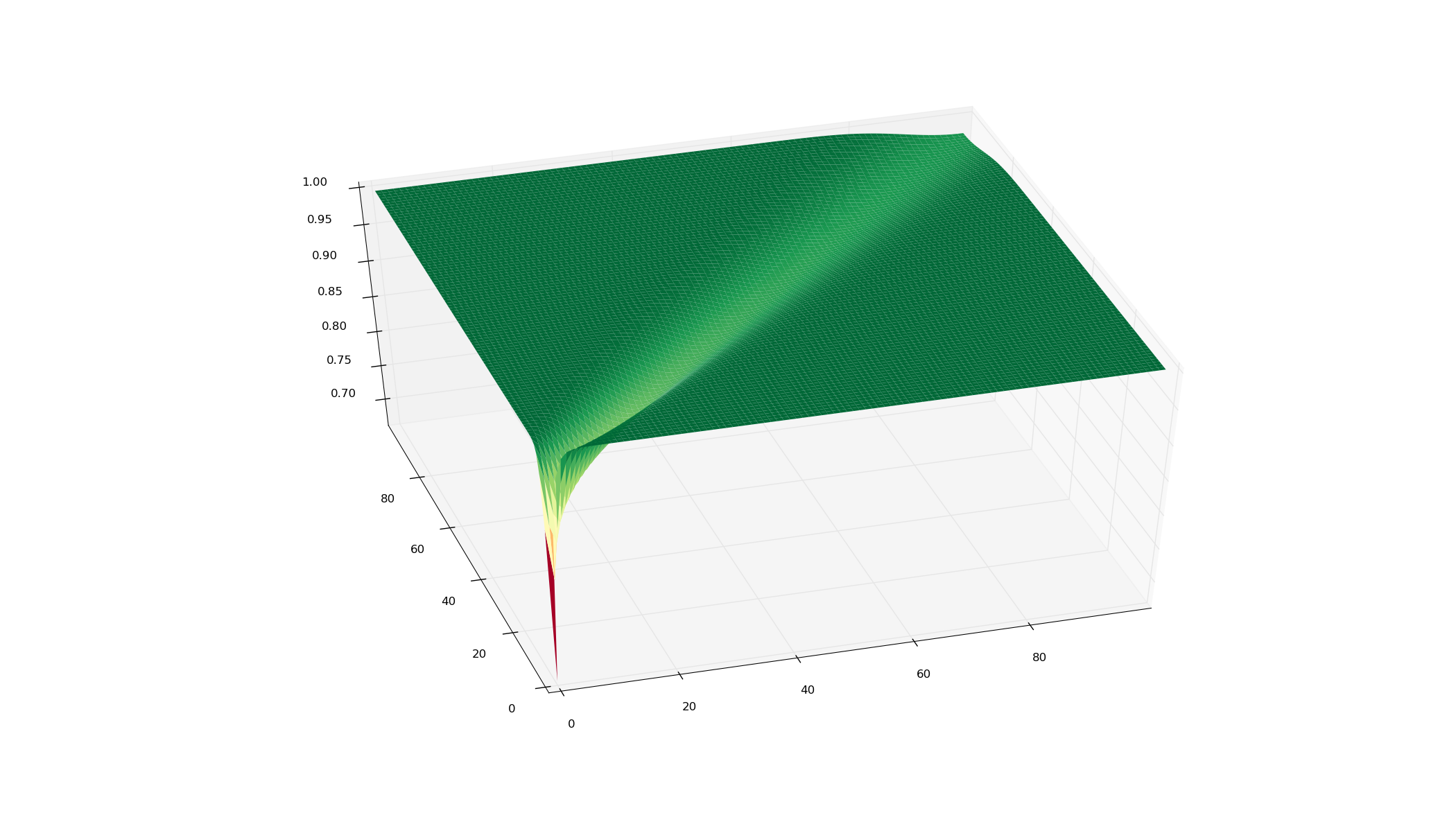
un dernier ajout, si vous cherchez à faire cela pour les grands nombres, alors vous allez avoir besoin de calculer les coefficients binomiaux d'une manière différente, comme vous allez déborder les entiers. Vos réponses sont lal flottant néanmoins, et puisque vous êtes apparemment intéressés par la grande f(n) = T(n,n) alors je suppose que vous pourriez utiliser L'approximation de Stirling ou quelque chose.
eh Bien pour commencer, voici quelques choses à garder à l'esprit:
cette condition ne peut se produire qu'une seule fois, mais vous la testez à chaque fois à travers chaque boucle.
if (x == 0 && y == 0) {
matrix[x][y] = 0;
}
Vous devez à la place: matrix[0][0] = 0; juste avant d'entrer dans votre première boucle et de mettre x à 1. Puisque vous savez que x ne sera jamais 0 vous pouvez supprimer la première partie de votre deuxième condition x == 0:
for(int x = 1; x <= i; x++)
{
for(int y = 0; y <= j; y++)
{
if (y == 0) {
matrix[x][y] = 1;
}
else
matrix[x][y] = (matrix[x-1][y] + matrix[x-1][y-1] + matrix[x][y-1])/3;
}
}
aucun point à déclarer ligne et Colonne puisque vous ne l'utilisez qu'une fois. double[][] matrix = new double[i+1][j+1];
Cet algorithme a une complexité minimale de Ω(n) parce que vous avez juste besoin de multiplier les valeurs dans la première colonne et la rangée de la matrice avec quelques facteurs et puis les additionner. Les facteurs proviennent du déroulement de la récursion n fois.
vous devez donc procéder à la décompression de la récursion. Cela en soi a une complexité de O(n^2). Mais en équilibrant déroulement et évaluation de la récursion, vous devriez être en mesure de réduire la complexité à O(n^x) où 1 <= x <= 2. Il s'agit d'une sorte de similitude avec les algorithmes pour la multiplication matrice-matrice, où le cas naïf a une complexité de O(n^3) mais L'algorithme de Strassens est par exemple O(n^2.807).
un autre point est le fait que la formule originale utilise un facteur de 1/3. Comme ceci n'est pas correctement représenté par des nombres de points fixes ou des points flottants ieee 754, l'erreur augmente lors de l'évaluation successive de la récursion. Donc dénouement de la récursivité pourrait vous donner plus grande précision comme un effet secondaire agréable.
Par exemple, lorsque vous déroulez la récursivité sqr(n) fois alors vous avez la complexité O((sqr(n))^2+(n/sqr(n))^2). La première partie est pour la détente et la deuxième partie est pour l'évaluation d'une nouvelle matrice de taille n/sqr(n). Cette nouvelle complexité peut en fait être simplifiée à O(n).
pour décrire la complexité du temps, nous utilisons habituellement une notation big O. Il est important de se rappeler qu'il ne décrit que la croissance donnée à l'intrant. O (n) est la complexité linéaire du temps, mais il ne dit pas à quelle vitesse (ou lentement) le temps croît quand nous augmentons l'entrée. Par exemple:
n=3 -> 30 seconds
n=4 -> 40 seconds
n=5 -> 50 seconds
C'est O(n), on voit clairement que chaque augmentation de n augmente le temps de 10 Secondes.
n=3 -> 60 seconds
n=4 -> 80 seconds
n=5 -> 100 seconds
C'est aussi O(n), même si pour chaque n Nous avons besoin de deux fois plus de temps, et l'augmentation est de 20 secondes pour chaque augmentation de n, la complexité de temps augmente linéairement.
donc si vous avez o(n*n) la complexité du temps et que vous réduisez de moitié le nombre d'opérations que vous effectuez, vous obtiendrez O(0.5*n*n) Qui est égal à O (n*n) - c.-à-d. que votre complexité du temps ne changera pas.
c'est une théorie, en pratique le nombre d'opérations fait parfois une différence. Parce que vous avez une grille n par n, Vous avez besoin de remplir n * n cellules, de sorte que la meilleure complexité de temps que vous pouvez atteindre est O(n*n), mais il y a quelques optimisations que vous pouvez faire:
- Cellules sur les bords de la grille pourrait être rempli de plusieurs boucles. Actuellement dans la majorité des cas, vous avez deux conditions inutiles pour i et j égale à 0.
- Vous grille a une ligne de symétrie, vous pouvez l'utiliser pour calculer seulement la moitié et ensuite copier le résultat sur l'autre moitié. Pour chaque i et j
grid[i][j] = grid[j][i]
en conclusion, la clarté et la lisibilité du code est beaucoup plus important que les performances - si vous pouvez lire et comprendre le code, vous pouvez le changer, mais si le code est tellement moche que vous ne pouvez pas comprendre, vous ne pouvez pas optimiser. C'est pourquoi je ne ferais que la première optimisation (qui augmente aussi la lisibilité), mais pas la deuxième - cela rendrait le code beaucoup plus difficile à comprendre.
en règle générale, n'optimisez pas le code, à moins que la performance ne cause vraiment des problèmes. Comme William Wulf dit:
plus de péchés informatiques sont commis au nom de l'efficacité (sans nécessairement l'atteindre) que pour toute autre raison - y compris la stupidité aveugle.
EDIT:
je pense qu'il peut être possible de mettre en œuvre cette fonction avec O(1) de la complexité. Bien qu'il ne donne aucun avantage quand vous avez besoin de remplir la grille entière, avec O (1) complexité de temps vous pouvez obtenir instantanément n'importe quelle valeur sans avoir une grille à tout.
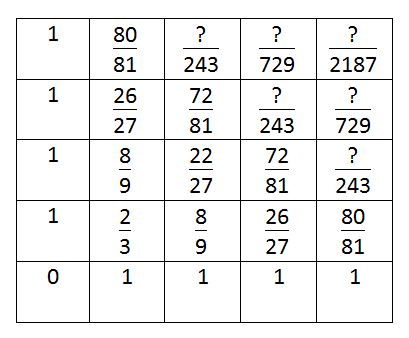
quelques remarques:
- le dénominateur est égal à
3 ^ (i + j - 1) - si i = 2 j = 2, le numérateur est inférieur au dénominateur
EDIT 2:
Le numérateur peut être exprimé avec la fonction suivante:
public static int n(int i, int j) {
if (i == 1 || j == 1) {
return 1;
} else {
return 3 * n(i - 1, j - 1) + n(i - 1, j) + n(i, j - 1);
}
}
très similaire au problème original, mais aucune division et tous les nombres sont entiers.
si la question Est de savoir comment afficher toutes les valeurs de la fonction pour 0<=i<N,0<=j<N, voici une solution dans le temps O(N²) et de l'espace O(N). Le comportement temporel est optimal.
Use a temporary array T of N numbers and set it to all ones, except for the first element.
Then row by row,
use a temporary element TT and set it to 1,
then column by column, assign simultaneously T[I-1], TT = TT, (TT + T[I-1] + T[I])/3.
grâce à la réponse de will (premier), j'ai eu cette idée:
considérez que toute solution positive vient seulement de 1's le long de la x et y axes. Chacun des appels récursifs f divise chaque composante de la solution par 3, ce qui signifie que nous pouvons additionner, combinatoire, combien de façons chacune 1 comme composante de la solution, et considérer sa "distance" (mesurée comme le nombre d'appels de f il est de la cible) comme un pouvoir négatif de 3.
code JavaScript:
function f(n){
var result = 0;
for (var d=n; d<2*n; d++){
var temp = 0;
for (var NE=0; NE<2*n-d; NE++){
temp += choose(n,NE);
}
result += choose(d - 1,d - n) * temp / Math.pow(3,d);
}
return 2 * result;
}
function choose(n,k){
if (k == 0 || n == k){
return 1;
}
var product = n;
for (var i=2; i<=k; i++){
product *= (n + 1 - i) / i
}
return product;
}
Sortie:
for (var i=1; i<8; i++){
console.log("F(" + i + "," + i + ") = " + f(i));
}
F(1,1) = 0.6666666666666666
F(2,2) = 0.8148148148148148
F(3,3) = 0.8641975308641975
F(4,4) = 0.8879743941472337
F(5,5) = 0.9024030889600163
F(6,6) = 0.9123609205913732
F(7,7) = 0.9197747256986194