Algorithme pour calculer un diagramme de Voronoi sur une sphère?

mise à jour en juillet 2016:

grâce à un certain nombre de volontaires (en particulier Nikolai Nowaczyk et I), il existe maintenant un code beaucoup plus robuste / correct pour manipuler les diagrammes de Voronoi à la surface d'une sphère en Python. C'est officiellement disponible en scipy.spatial.SphericalVoronoi à partir de la version 0.18 à partir de scipy. Il y a un exemple pratique d'usage et de traçage dans l'official docs.

L'algorithme suit complexité quadratique du temps. Tandis que loglinear est le théorique optimum pour les diagrammes de Voronoi sur les surfaces de sphères, c'est actuellement le meilleur que nous avons pu mettre en œuvre. Si vous souhaitez en savoir plus et contribuer à l'effort de développement, il y a quelques problèmes en suspens liés à l'amélioration de la façon dont Python gère les diagrammes sphériques de Voronoi et les structures de données connexes:

• Effort pour améliorer le tracé des polygones sphériques dans matplotlib
• Effort pour améliorer la manipulation de Sphérique calcul de la surface des polygones en scipy

pour plus d'informations sur la théorie / le développement / les défis liés à ce code Python et les efforts de géométrie computationnelle associés, vous pouvez également consulter quelques conférences de Nikolai et moi:

• Nikolai PyData Londres 2016 parler
• Tyler PyData London 2015 talk
• Tyler PyCon Géométrie Computationnelle 2016 tutoriel

Réponse Originale:

j'ai en fait récemment écrit un code Python open source pour les diagrammes de Voronoi à la surface d'une sphère:https://github.com/tylerjereddy/py_sphere_Voronoi

L'utilisation, l'algorithme, et les limites sont documentées sur readthedocs (http://py-sphere-voronoi.readthedocs.org/en/latest/voronoi_utility.html). Il y a quelques exemples détaillés de là, mais je vais placez un ou deux ci-dessous. Le module traite également le calcul des surfaces de la région du Voronoi, avec quelques faiblesses numériques dans la version de développement actuelle.

Je n'ai pas vu beaucoup d'implémentations open source bien documentées pour des diagrammes Voronoï sphériques, mais il y a eu un peu de buzz sur L'implémentation JavaScript sur le site de Jason Davies (http://www.jasondavies.com/maps/voronoi/). Je ne pense pas que son code soit ouvert. J'ai aussi j'ai vu un billet de blog sur L'utilisation de Python pour traiter une partie du problème (http://jellymatter.com/2014/01/29/voronoi-tessellation-on-the-surface-of-a-sphere-python-code/). Bon nombre des sources documentaires primaires citées dans les articles précédents semblaient très difficiles à mettre en œuvre (j'en ai essayé quelques-unes), mais peut-être que certaines personnes trouveront ma mise en œuvre utile ou même suggéreront des moyens de l'améliorer.

Exemples:

1) produire un Voronoi schéma pour un pseudo-aléatoire de points sur la sphère unité:

import matplotlib
import matplotlib.pyplot as plt
import matplotlib.colors as colors
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import numpy as np
import scipy as sp
import voronoi_utility
#pin down the pseudo random number generator (prng) object to avoid certain pathological generator sets
prng = np.random.RandomState(117) #otherwise, would need to filter the random data to ensure Voronoi diagram is possible
#produce 1000 random points on the unit sphere using the above seed
random_coordinate_array = voronoi_utility.generate_random_array_spherical_generators(1000,1.0,prng)
#produce the Voronoi diagram data
voronoi_instance = voronoi_utility.Voronoi_Sphere_Surface(random_coordinate_array,1.0)
dictionary_voronoi_polygon_vertices = voronoi_instance.voronoi_region_vertices_spherical_surface()
#plot the Voronoi diagram
fig = plt.figure()
fig.set_size_inches(2,2)
ax = fig.add_subplot(111, projection='3d')
for generator_index, voronoi_region in dictionary_voronoi_polygon_vertices.iteritems():
   random_color = colors.rgb2hex(sp.rand(3))
   #fill in the Voronoi region (polygon) that contains the generator:
   polygon = Poly3DCollection([voronoi_region],alpha=1.0)
   polygon.set_color(random_color)
   ax.add_collection3d(polygon)
ax.set_xlim(-1,1);ax.set_ylim(-1,1);ax.set_zlim(-1,1);
ax.set_xticks([-1,1]);ax.set_yticks([-1,1]);ax.set_zticks([-1,1]); 
plt.tick_params(axis='both', which='major', labelsize=6)

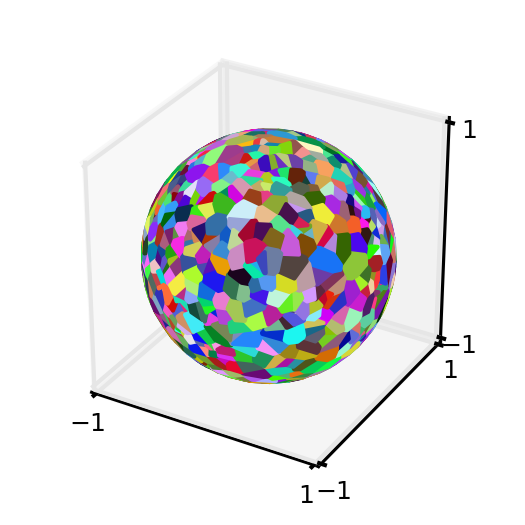
2) calculer les surfaces des polygones de la région de Voronoi et vérifier que la surface reconstituée est raisonnable:

import math
dictionary_voronoi_polygon_surface_areas = voronoi_instance.voronoi_region_surface_areas_spherical_surface()
theoretical_surface_area_unit_sphere = 4 * math.pi
reconstituted_surface_area_Voronoi_regions = sum(dictionary_voronoi_polygon_surface_areas.itervalues())
percent_area_recovery = round((reconstituted_surface_area_Voronoi_regions / theoretical_surface_area_unit_sphere) * 100., 5)
print percent_area_recovery
97.87551 #that seems reasonable for now

notez que la triangulation Delaunay sur une sphère n'est que la coque convexe. Ainsi, vous pouvez calculer la coque 3d convexe (par exemple en utilisant CGAL) et prendre le double.

En bref, essayer cssgrid Ncar Graphics. J'ai écrit plus de réponse pour une question similaire à codereview.stackexchange.com.

Il y a un papier D'INRIA sur la Triangulation de Delaunay (DT) de points situés sur une sphère: CAROLI, Manuel,et al. Triangulations Delaunay robustes et efficaces de points sur ou près d'une sphère. 2009. où ils parlent d'une implémentation en CGAL.

l'article fait référence à diverses implémentations disponibles d'algorithmes DT.

citation tirée du journal:

une réponse facile et standard consiste en calcul de la coque 3d convexe des points, ce qui est notoirement équivalent.

pour le calcul de l'enveloppe convexe, le document suggère:

1. Hull, un programme pour les coques convexes.
2. Qhull.
3. coques convexes tridimensionnelles. en FORTRAN.Des coques tridimensionnelles convexes.
4. STRIPACK en FORTRAN.

la classe DT C++ de CGAL a la méthode dual pour obtenir le diagramme de Voronoi.

Selon ce post par Monique Teillaud (l'une des auteures de l'article mentionné ci-dessus) il me semble qu'en novembre 2012 la mise en œuvre n'était pas encore prête.

Cela fait longtemps qu'on n'a pas répondu à la question, mais j'ai trouvé deux documents qui mettent en oeuvre algorithme de Fortune

• "Sweeping the Sphere" de Dinis et Mamede, publié dans le 2010 International Symposium on Voronoi Diagrammes in Science and Engineering. Peuvent être achetés à http://dx.doi.org/10.1109/ISVD.2010.32
• "Un Plan de Balayage de l'Algorithme pour la Tessellation de Voronoï de la Sphère" par Zheng et coll. Je ne suis pas sûr qu'il ait été publié en raison de la première, mais il est daté du 13 décembre 2011. Il est disponible gratuitement sur http://www.e-lc.org/tmp/Xiaoyu__Zheng_2011_12_05_14_35_11.pdf

j'y travaille moi-même en ce moment, donc je ne peux pas bien l'expliquer. L'idée de base est que L'algorithme de Fortune fonctionne à la surface de la sphère tant que vous calculez correctement les paraboles de limite des points. Parce que la surface des enveloppes de sphère, vous pouvez également utiliser une liste circulaire pour contenir la ligne de plage et ne vous inquiétez pas de manipuler des cellules au bord de l'espace rectangulaire. Avec cela, vous pouvez balayer à partir du pôle Nord de la sphère au sud et remonter à nouveau, sautant à des sites qui introduisent de nouveaux points à la ligne de plage (ajoutant une parabole à la ligne de plage) ou l'introduction de la cellule sommets (retrait d'une parabole de la ligne de plage).

les deux articles s'attendent à un niveau élevé de confort avec l'algèbre linéaire pour comprendre les concepts, et ils continuent tous les deux de me perdre au point où ils commencent à expliquer l'algorithme lui-même. Ni l'un ni l'autre ne fournissent de code source, malheureusement.

je pense que le plan de Voronoi pour chaque point peut être construit en utilisant la géométrie non-euclidienne. Ce qui était normalement une ligne sur un plan 2d, est maintenant un "grand cercle" sur la sphère (voir Wikipedia:géométrie elliptique