Algorithme pour créer des coins arrondis dans un polygone
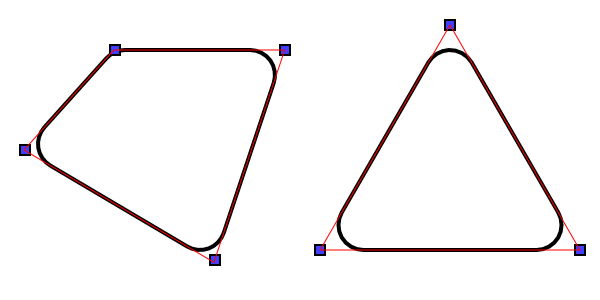
je cherche un algorithme qui me permet de créer des coins arrondis à partir d'un polygone. En Entrée, j'obtiens un tableau de points qui représente le polygone (ligne rouge) et en sortie, un tableau de points qui représente le polygone avec des coins arrondis (ligne noire).
je voudrais aussi avoir un moyen de contrôler le rayon de chaque coin. J'ai déjà essayé D'utiliser Bezier et Subdivision mais ce n'est pas ce que je cherche. Bezier et la Subdivision lissent tout le polygone. Ce Que Je ça ne fait que arrondir les coins.
Quelqu'un connaît un bon algorithme pour le faire? Je travaille en C# mais le code doit être indépendant de toute bibliothèque .NET.
5 réponses
Certains géométrie avec de la Peinture:
0. Vous disposez d'un coin: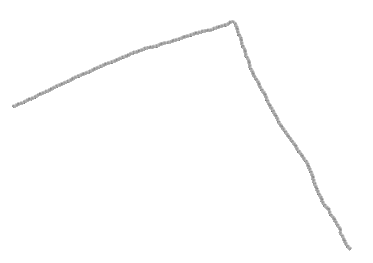
1. Vous connaissez les coordonnées des points d'angle, laissez-Le être P1, P2 et P: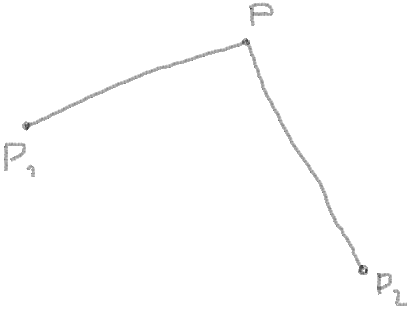
2. Maintenant vous pouvez obtenir des vecteurs de points et d'angle entre vecteurs: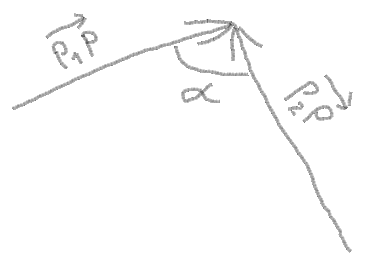
angle = atan(PY - P1Y, PX - P1X) - atan(PY - P2Y, PX - P2X)
3. Obtenez la longueur du segment entre le point angulaire et les points d'intersection avec le cercle.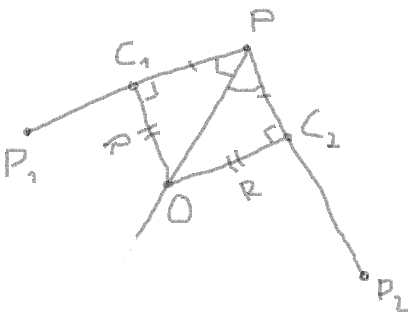
segment = PC1 = PC2 = radius / |tan(angle / 2)|
4. Ici, vous devez vérifier la longueur de segment et la longueur minimale de PP1 et PP2: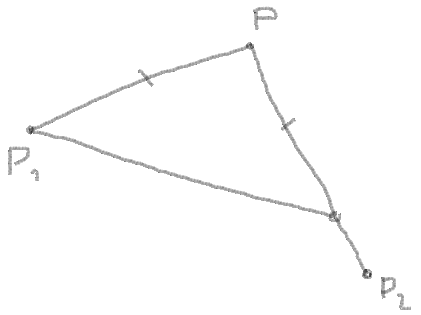
Longueur de PP1:
PP1 = sqrt((PX - P1X)2 + (PY - P1Y)2)
Longueur de PP2:
PP2 = sqrt((PX - P2X)2 + (PY - P2Y)2)
si segment > PP1 ou segment > PP2 alors vous devez diminuer le rayon:
min = Min(PP1, PP2) (for polygon is better to divide this value by 2)
segment > min ?
segment = min
radius = segment * |tan(angle / 2)|
5. Obtenir la longueur de la PO:
PO = sqrt(radius2 + segment2)
6. Obtenez le C1 X et C1O par la proportion entre la coordonnées du vecteur, longueur du vecteur et longueur du segment: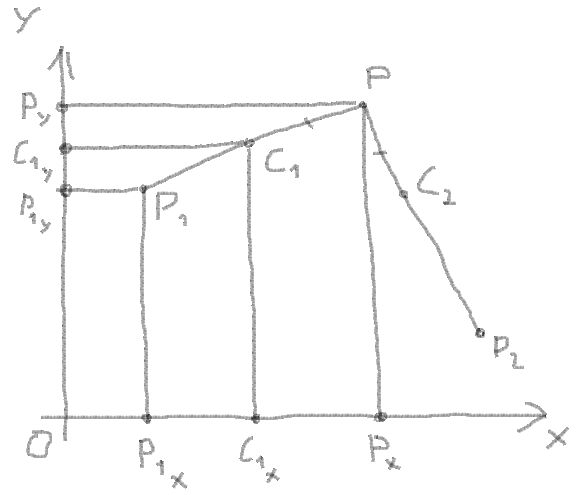
Proportion:
(PX - C1X) / (PX - P1X) = PC1 / PP1
Donc:
C1X = PX - (PX - P1X) * PC1 / PP1
idem pour C1O:
C1Y = PY - (PY - P1Y) * PC1 / PP1
7. Obtenez le C2 X et C2O de la même manière:
C2X = PX - (PX - P2X) * PC2 / PP2 C2Y = PY - (PY - P2Y) * PC2 / PP2
8. Maintenant, vous peut utiliser l'ajout de vecteurs PC1 et PC2 pour trouver le centre du cercle par le même chemin par la proportion: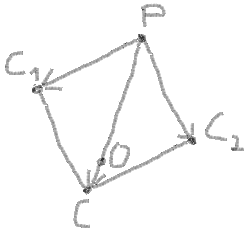
(PX - OX) / (PX - CX) = PO / PC (PY - OY) / (PY - CY) = PO / PC
Ici:
CX = C1X + C2X - PX CY = C1Y + C2Y - PY PC = sqrt((PX - CX)2 + (PY - CY)2)
:
dx = PX - CX = PX * 2 - C1X - C2X dy = PY - CY = PY * 2 - C1Y - C2Y
Donc:
PC = sqrt(dx2 + dy2) OX = PX - dx * PO / PC OY = PY - dy * PO / PC
9. Ici, vous pouvez dessiner un arc. Pour cela, vous devez obtenir l'angle de début et l'angle d'extrémité de l'arc: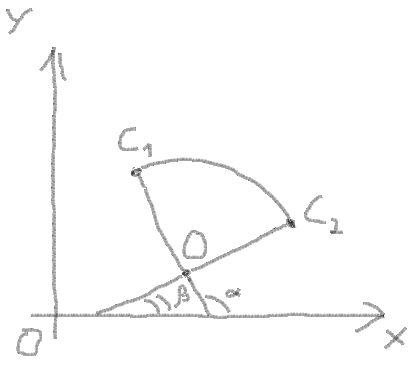
Trouvé ici:
startAngle = atan((C1Y - OY) / (C1X - OX)) endAngle = atan((C2Y - OY) / (C2X - OX))
10. Enfin vous devez obtenir un angle de balayage et faire quelques vérifications pour elle: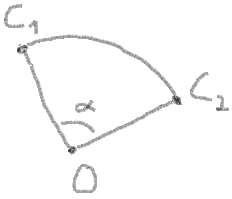
sweepAngle = endAngle - startAngle
Si sweepAngle < 0 alors swap startAngle et endAngle, et inverser sweepAngle:
sweepAngle < 0 ?
sweepAngle = - sweepAngle
startAngle = endAngle
Vérifier si sweepAngle > 180 degrés:
sweepAngle > 180 ?
sweepAngle = 180 - sweepAngle
11. Et maintenant vous pouvez dessiner un arrondi coin:
Certains de la géométrie avec c#:
private void DrawRoundedCorner(Graphics graphics, PointF angularPoint,
PointF p1, PointF p2, float radius)
{
//Vector 1
double dx1 = angularPoint.X - p1.X;
double dy1 = angularPoint.Y - p1.Y;
//Vector 2
double dx2 = angularPoint.X - p2.X;
double dy2 = angularPoint.Y - p2.Y;
//Angle between vector 1 and vector 2 divided by 2
double angle = (Math.Atan2(dy1, dx1) - Math.Atan2(dy2, dx2)) / 2;
// The length of segment between angular point and the
// points of intersection with the circle of a given radius
double tan = Math.Abs(Math.Tan(angle));
double segment = radius / tan;
//Check the segment
double length1 = GetLength(dx1, dy1);
double length2 = GetLength(dx2, dy2);
double length = Math.Min(length1, length2);
if (segment > length)
{
segment = length;
radius = (float)(length * tan);
}
// Points of intersection are calculated by the proportion between
// the coordinates of the vector, length of vector and the length of the segment.
var p1Cross = GetProportionPoint(angularPoint, segment, length1, dx1, dy1);
var p2Cross = GetProportionPoint(angularPoint, segment, length2, dx2, dy2);
// Calculation of the coordinates of the circle
// center by the addition of angular vectors.
double dx = angularPoint.X * 2 - p1Cross.X - p2Cross.X;
double dy = angularPoint.Y * 2 - p1Cross.Y - p2Cross.Y;
double L = GetLength(dx, dy);
double d = GetLength(segment, radius);
var circlePoint = GetProportionPoint(angularPoint, d, L, dx, dy);
//StartAngle and EndAngle of arc
var startAngle = Math.Atan2(p1Cross.Y - circlePoint.Y, p1Cross.X - circlePoint.X);
var endAngle = Math.Atan2(p2Cross.Y - circlePoint.Y, p2Cross.X - circlePoint.X);
//Sweep angle
var sweepAngle = endAngle - startAngle;
//Some additional checks
if (sweepAngle < 0)
{
startAngle = endAngle;
sweepAngle = -sweepAngle;
}
if (sweepAngle > Math.PI)
sweepAngle = Math.PI - sweepAngle;
//Draw result using graphics
var pen = new Pen(Color.Black);
graphics.Clear(Color.White);
graphics.SmoothingMode = SmoothingMode.AntiAlias;
graphics.DrawLine(pen, p1, p1Cross);
graphics.DrawLine(pen, p2, p2Cross);
var left = circlePoint.X - radius;
var top = circlePoint.Y - radius;
var diameter = 2 * radius;
var degreeFactor = 180 / Math.PI;
graphics.DrawArc(pen, left, top, diameter, diameter,
(float)(startAngle * degreeFactor),
(float)(sweepAngle * degreeFactor));
}
private double GetLength(double dx, double dy)
{
return Math.Sqrt(dx * dx + dy * dy);
}
private PointF GetProportionPoint(PointF point, double segment,
double length, double dx, double dy)
{
double factor = segment / length;
return new PointF((float)(point.X - dx * factor),
(float)(point.Y - dy * factor));
}
Pour obtenir des points de l'arc, vous pouvez utiliser ceci:
//One point for each degree. But in some cases it will be necessary
// to use more points. Just change a degreeFactor.
int pointsCount = (int)Math.Abs(sweepAngle * degreeFactor);
int sign = Math.Sign(sweepAngle);
PointF[] points = new PointF[pointsCount];
for (int i = 0; i < pointsCount; ++i)
{
var pointX =
(float)(circlePoint.X
+ Math.Cos(startAngle + sign * (double)i / degreeFactor)
* radius);
var pointY =
(float)(circlePoint.Y
+ Math.Sin(startAngle + sign * (double)i / degreeFactor)
* radius);
points[i] = new PointF(pointX, pointY);
}
vous recherchez un arc tangent à deux segments de ligne connectés, d'un rayon donné, donné par un tableau séquentiel de points. algorithme pour trouver cet arc est comme suit:
pour chaque segment, construire un vecteur normal.
Si vous travaillez en 2d, vous pouvez juste soustraire les deux extrémités pour obtenir un vecteur tangent (X, Y). Dans ce cas, les vecteurs normaux seront plus ou moins (-Y, X). Normaliser le vecteur normal à la longueur. Enfin, choisissez la direction avec un produit à points positifs avec le vecteur tangent du segment suivant. ( voir Mise à jour ci-dessous