Graphique 3D avec Matplotlib
j'essaye simplement de tracer une surface et son contour en 3D, exactement comme dans exemple.
voici le code que j'utilise pour le faire:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import numpy
def plot_3d_contour(x_dim, y_dim, x_steps, y_steps, scalar_field, file_path):
fig = plt.figure()
x, y = numpy.mgrid[-x_dim/2:x_dim/2:x_steps*1j, -y_dim/2:y_dim/2:y_steps*1j]
v_min = numpy.min(scalar_field)
v_max = nupmy.max(scalar_field)
ax = fig.gca(projection='3d')
cset = ax.contourf(x, y, scalar_field, zdir='z', offset=v_min, cmap=cm.coolwarm)
cset = ax.contourf(x, y, scalar_field, zdir='x', offset=-x_dim/2-1, cmap=cm.coolwarm)
cset = ax.contourf(x, y, scalar_field, zdir='y', offset=y_dim/2+1, cmap=cm.coolwarm)
ax.plot_surface(x, y, scalar_field, rstride=10, cstride=10, alpha=0.3)
ax.set_xlabel('X')
ax.set_xlim(-x_dim/2-1, x_dim/2+1)
ax.set_ylabel('Y')
ax.set_ylim(-y_dim/2-1, y_dim/2+1)
ax.set_zlabel('Z')
ax.set_zlim(v_min, v_max)
plt.savefig(file_path + '.jpg')
plt.close()
scalar_field = numpy.loadtxt('../scalar_field', delimiter=",")
plot_3d_contour(12, 12, 100, 100, scalar_field, 'scalar_field3D')
Cependant, je vais avoir un comportement bizarre dans lequel le contour (zdir=y) est au-dessus de la surface. En plus, j'ai un contour bizarre en z_dir=z (avec un article manquant):
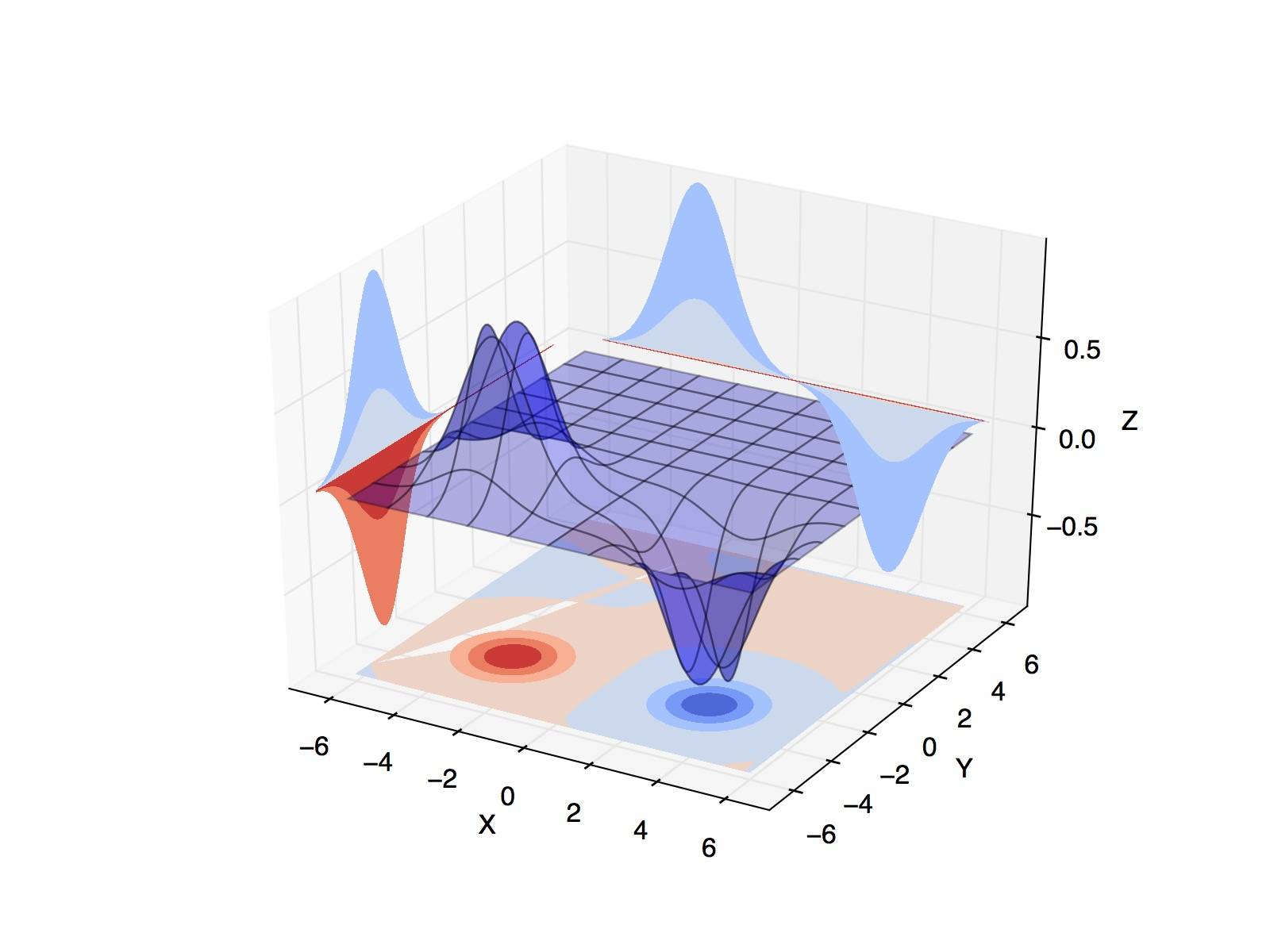
je me demande ce que je rate. Le champ scalaire peut être trouvé ici.
1 réponses
Je suis D'accord avec Ajean. Je crois que le problème se pose parce que l'artiste de chaque matplotlib (c.-à-d. PolygonCollection) est rendu séparément. Il n'y a aucun moyen que des visages différents du même objet soient rendus sur des côtés différents d'un autre objet de la scène.
voici un code utile:
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np
file_path = "./3D_surface_and_contour.jpg"
p = 0.05
f = -0.01
def get_data(p):
x, y, z = axes3d.get_test_data(p)
z = f * z
return x, y, z
def plot_3d_contour(p, f):
nrows = 4
ncols = 5
x, y, z = get_data(p)
x_min, x_max = np.min(x), np.max(x)
y_min, y_max = np.min(y), np.max(y)
z_min, z_max = np.min(z), np.max(z)
fig = plt.figure(figsize=(15, 10))
for n in range(nrows * ncols):
i = n % ncols
j = n / ncols
k = n + 1
if j == 0:
azim = -60 + (i - 2) * 15
elev = 30
elif j == 1:
azim = -60
elev = 30 + (i - 2) * 5
elif j == 2:
azim = 60 + (i - 2) * 10
elev = 30
elif j == 3:
azim = 60
elev = 30 + (i - 2) * 5
ax = fig.add_subplot(nrows, ncols, k, projection='3d')
ax.set_title("azim=" + str(azim) + " elev=" + str(elev))
ax.tick_params(labelsize=8)
ax.view_init(azim=azim, elev=elev)
ax.plot_surface(x, y, z, rstride=10, cstride=10, alpha=0.3)
ax.contourf(x, y, z, zdir='z', offset=z_min, cmap=cm.coolwarm)
ax.contourf(x, y, z, zdir='x', offset=x_min, cmap=cm.coolwarm)
if j == 0 or j == 1:
ax.contourf(x, y, z, zdir='y', offset=y_max, cmap=cm.coolwarm)
elif j == 2 or j == 3:
ax.contourf(x, y, z, zdir='y', offset=y_min, cmap=cm.coolwarm)
ax.set_xlabel('X')
ax.set_xlim(x_min, x_max)
ax.set_ylabel('Y')
ax.set_ylim(y_min, y_max)
ax.set_zlabel('Z')
ax.set_zlim(z_min, z_max)
plt.savefig(file_path, dpi=80)
plt.close()
plot_3d_contour(p, f)
ce qui donne l'image suivante :
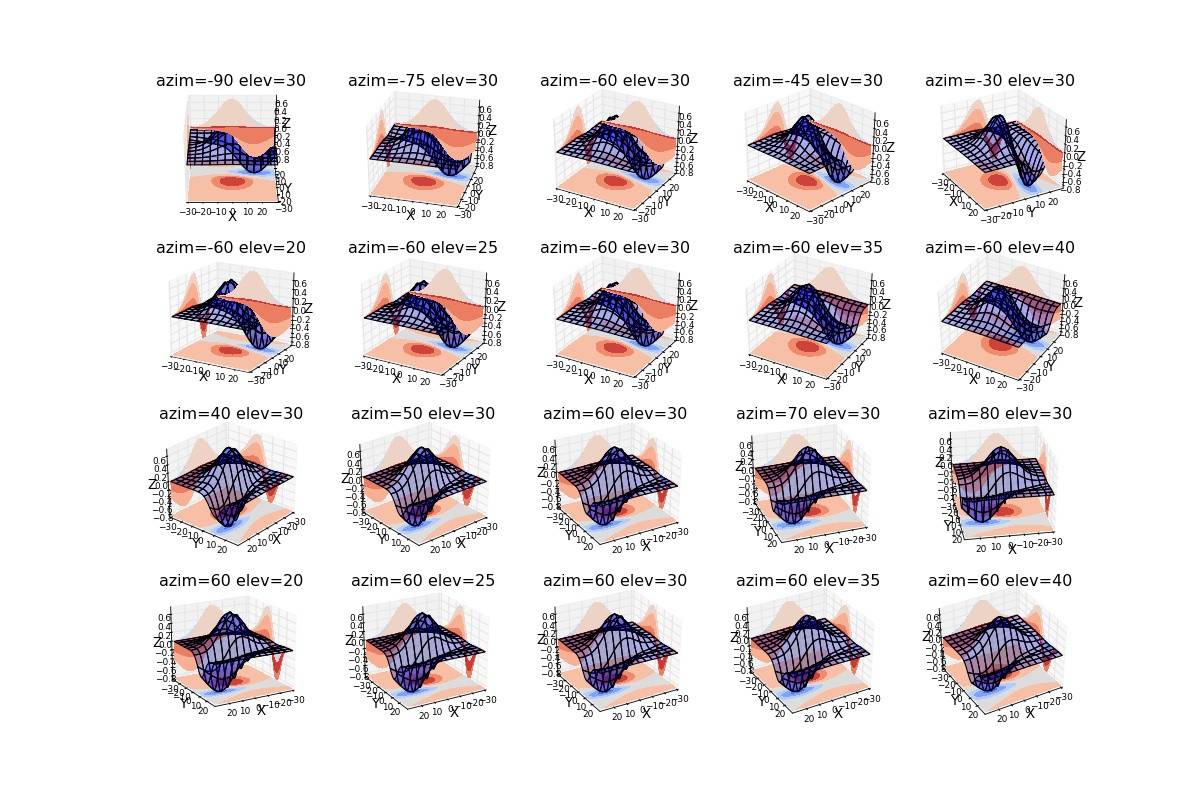
les deux premières lignes sont produites par un code similaire au vôtre. Vous pourriez remarquer que réglage de l'altitude avec view_init à une valeur supérieure résolvez le problème. Mais il n'est pas satisfaisant. J'ai également déterminé l'influence de la gamme de valeurs z (non montré ici), le bug semble s'affichent uniquement lorsque cette plage est petite (vous pouvez utiliser le f paramètre pour le tester) qui explique pourquoi le exemple n'en souffre pas.
la solution que je propose est de remplacer :
ax.contourf(x, y, scalar_field, zdir='y', offset=y_dim/2+1, cmap=cm.coolwarm)
par :
ax.contourf(x, y, scalar_field, zdir='y', offset=-y_dim/2-1, cmap=cm.coolwarm)
dans votre code et ajouter cette ligne supplémentaire :
ax.view_init(azim=60, elev=30)
comme indiqué dans les deux dernières lignes de l'image précédente, vous pourrez ainsi éviter les caprices de matplotlib.