3D Plan des moindres carrés

sauf si quelqu'un me dit comment taper des équations ici, laissez-moi juste écrire les derniers calculs que vous avez à faire:

d'abord, compte tenu des points r_i \n \r, i=1..N, calculer le centre de masse de tous les points:

r_G = \frac{\sum_{i=1}^N r_i}{N}

ensuite, calculer le vecteur normal n, Qui avec le vecteur de base r_G définit le plan en calculant la matrice 3x3 A comme

A = \sum_{i=1}^N (r_i - r_G)(r_i - r_G)^T

avec cette matrice, le vecteur normal n est maintenant donnée par le secteur propre d'une valeur propre correspondant à la valeur propre minimale de A.

pour en savoir plus sur les paires eigenvector/eigenvalue, utilisez n'importe quelle bibliothèque d'algèbre linéaire de votre choix.

cette solution est basée sur le théorème de Rayleight-Ritz pour la matrice hermitienne A.

voir "ajustement des données par les moindres carrés" par David Eberly pour savoir comment j'ai trouvé celui-ci pour minimiser l'ajustement géométrique (distance orthogonale des points au plan).

bool Geom_utils::Fit_plane_direct(const arma::mat& pts_in, Plane& plane_out)
{
    bool success(false);
    int K(pts_in.n_cols);
    if(pts_in.n_rows == 3 && K > 2)  // check for bad sizing and indeterminate case
    {
        plane_out._p_3 = (1.0/static_cast<double>(K))*arma::sum(pts_in,1);
        arma::mat A(pts_in);
        A.each_col() -= plane_out._p_3; //[x1-p, x2-p, ..., xk-p]
        arma::mat33 M(A*A.t());
        arma::vec3 D;
        arma::mat33 V;
        if(arma::eig_sym(D,V,M))
        {
            // diagonalization succeeded
            plane_out._n_3 = V.col(0); // in ascending order by default
            if(plane_out._n_3(2) < 0)
            {
                plane_out._n_3 = -plane_out._n_3; // upward pointing
            }
            success = true;
        }
    }
    return success;
}

Chronométré à 37 micro-secondes montage d'un avion à 1000 points (Windows 7, i7, programme 32 bits)

comme pour toute approche par la méthode des moindres carrés, vous procédez comme suit:

avant de commencer à coder

1. notez une équation pour un plan dans une certaine paramétrisation, dites 0 = ax + by + z + d dans les paramètres (a, b, d) .

2. trouver une expression D(\vec{v};a, b, d) pour la distance à partir d'un point arbitraire \vec{v} .

3. Notez la somme S = \sigma_i=0,n D^2(\vec{x}_i) , et simplifiez jusqu'à ce qu'elle soit exprimée en termes de sommes simples des composants de v comme \sigma v_x , \sigma v_y^2 , \sigma v_x*v_z ...

4. noter les expressions de minimisation par paramètre dS/dx_0 = 0 , dS/dy_0 = 0 ... ce qui vous donne un ensemble de trois équations à trois paramètres et les sommes provenant de l'étape précédente.

5. résolvez cet ensemble de les équations pour les paramètres.

(ou pour les cas simples, consultez le formulaire). Utiliser un paquet d'algèbre symbolique (comme Mathematica) pourrait vous faciliter la vie.

le codage

• écrire le code pour former les sommes nécessaires et trouver les paramètres de la dernière série ci-dessus.

Alternatives

notez que si vous avez réellement eu seulement trois points, vous feriez mieux de trouver l'avion qui les traverse.

aussi, si la solution analytique dans unfeasible (pas le cas d'un plan, mais possible en général), vous pouvez faire les étapes 1 et 2, et utiliser un Monte Carlo minimizer sur la somme à l'étape 3.

CGAL::linear_least_squares_fitting_3

fonction linear_least_squares_fitting_3 calcule le meilleur ajustement 3D ligne ou plan (au sens des moindres carrés) d'un ensemble D'objets 3D tels comme points, segments, triangles, sphères, boules, cuboïdes ou tétraèdres.

http://www.cgal.org/Manual/latest/doc_html/cgal_manual/Principal_component_analysis_ref/Function_linear_least_squares_fitting_3.html

l'équation pour un plan est: ax + by + c= Z. Donc, mettez en place des matrices comme celle-ci avec toutes vos données:

    x_0   y_0   1  
A = x_1   y_1   1  
          ... 
    x_n   y_n   1  

et

    a  
x = b  
    c

et

    z_0   
B = z_1   
    ...   
    z_n

en d'autres termes: Ax = B. maintenant, résolvez pour x qui sont vos coefficients. Mais puisque (je suppose) vous avez plus de 3 points, le système est sur-déterminé donc vous devez utiliser le pseudo inverse Gauche. La réponse est donc:

a 
b = (A^T A)^-1 A^T B
c

Et voici un code Python simple avec un exemple:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

N_POINTS = 10
TARGET_X_SLOPE = 2
TARGET_y_SLOPE = 3
TARGET_OFFSET  = 5
EXTENTS = 5
NOISE = 5

# create random data
xs = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
ys = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
zs = []
for i in range(N_POINTS):
    zs.append(xs[i]*TARGET_X_SLOPE + \
              ys[i]*TARGET_y_SLOPE + \
              TARGET_OFFSET + np.random.normal(scale=NOISE))

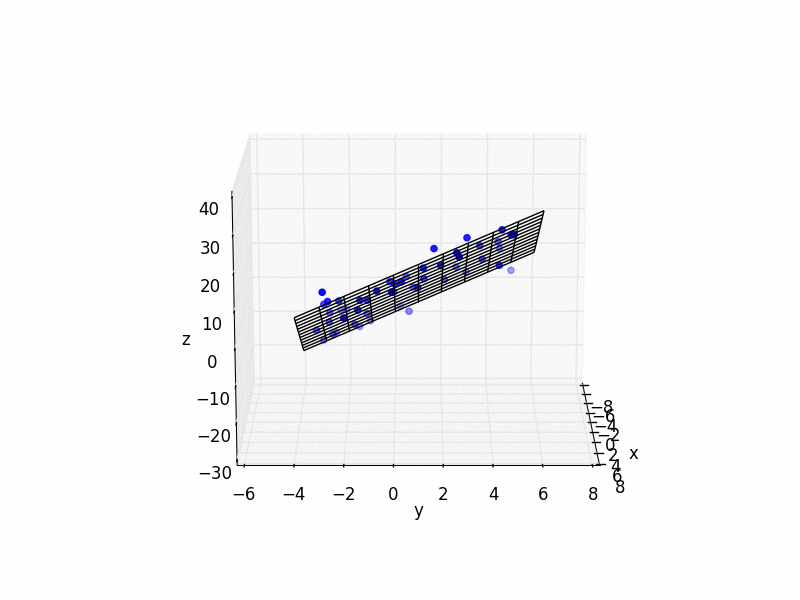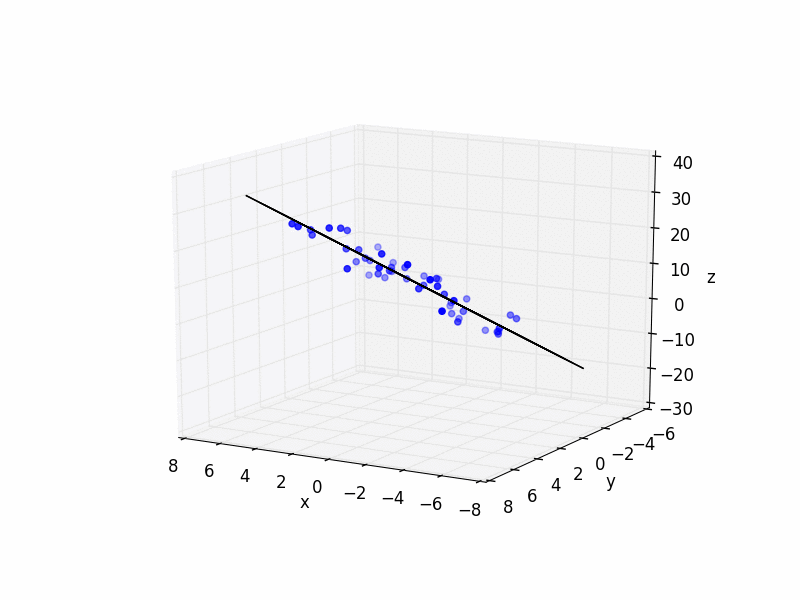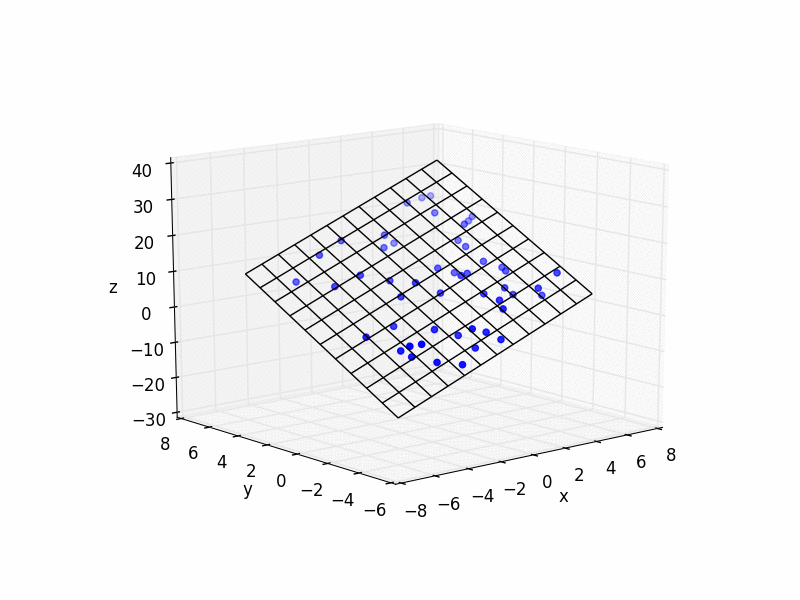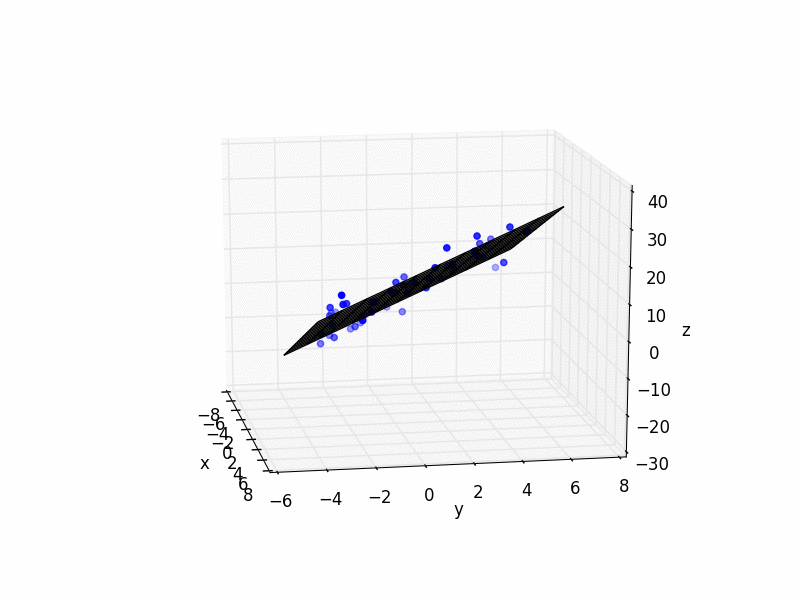
# plot raw data
plt.figure()
ax = plt.subplot(111, projection='3d')
ax.scatter(xs, ys, zs, color='b')

# do fit
tmp_A = []
tmp_b = []
for i in range(len(xs)):
    tmp_A.append([xs[i], ys[i], 1])
    tmp_b.append(zs[i])
b = np.matrix(tmp_b).T
A = np.matrix(tmp_A)
fit = (A.T * A).I * A.T * b
errors = b - A * fit
residual = np.linalg.norm(errors)

print "solution:"
print "%f x + %f y + %f = z" % (fit[0], fit[1], fit[2])
print "errors:"
print errors
print "residual:"
print residual

# plot plane
xlim = ax.get_xlim()
ylim = ax.get_ylim()
X,Y = np.meshgrid(np.arange(xlim[0], xlim[1]),
                  np.arange(ylim[0], ylim[1]))
Z = np.zeros(X.shape)
for r in range(X.shape[0]):
    for c in range(X.shape[1]):
        Z[r,c] = fit[0] * X[r,c] + fit[1] * Y[r,c] + fit[2]
ax.plot_wireframe(X,Y,Z, color='k')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

Tout ce que vous aurez à faire est de résoudre le système d'équations.

si ce sont vos points: (1, 2, 3), (4, 5, 6), (7, 8, 9)

qui vous donne les équations:

3=a*1 + b*2 + c
6=a*4 + b*5 + c
9=a*7 + b*8 + c

donc votre question devrait être en fait: comment résoudre un système d'équations?

donc je recommande la lecture cette donc question.

si j'ai mal compris votre question laissez-nous savoir.

MODIFIER :

ignorez ma réponse car vous vouliez probablement dire autre chose.

il semble que tout ce que vous voulez faire est une régression linéaire avec 2 régresseurs. La page de wikipedia sur le sujet devrait vous dire tout ce que vous avez besoin de savoir et puis un peu.

cela réduit au total des moindres carrés problème, qui peut être résolu en utilisant SVD décomposition.

code C++ à l'aide d'OpenCV:

float fitPlaneToSetOfPoints(const std::vector<cv::Point3f> &pts, cv::Point3f &p0, cv::Vec3f &nml) {
    const int SCALAR_TYPE = CV_32F;
    typedef float ScalarType;

    // Calculate centroid
    p0 = cv::Point3f(0,0,0);
    for (int i = 0; i < pts.size(); ++i)
        p0 = p0 + conv<cv::Vec3f>(pts[i]);
    p0 *= 1.0/pts.size();

    // Compose data matrix subtracting the centroid from each point
    cv::Mat Q(pts.size(), 3, SCALAR_TYPE);
    for (int i = 0; i < pts.size(); ++i) {
        Q.at<ScalarType>(i,0) = pts[i].x - p0.x;
        Q.at<ScalarType>(i,1) = pts[i].y - p0.y;
        Q.at<ScalarType>(i,2) = pts[i].z - p0.z;
    }

    // Compute SVD decomposition and the Total Least Squares solution, which is the eigenvector corresponding to the least eigenvalue
    cv::SVD svd(Q, cv::SVD::MODIFY_A|cv::SVD::FULL_UV);
    nml = svd.vt.row(2);

    // Calculate the actual RMS error
    float err = 0;
    for (int i = 0; i < pts.size(); ++i)
        err += powf(nml.dot(pts[i] - p0), 2);
    err = sqrtf(err / pts.size());

    return err;
}